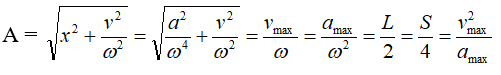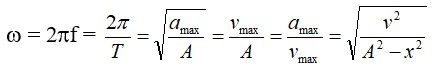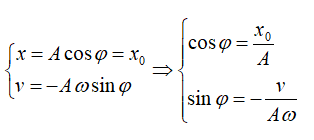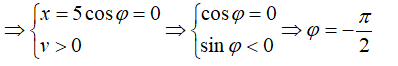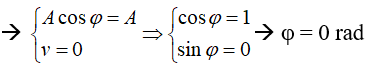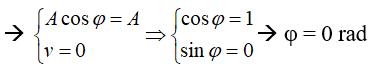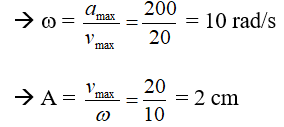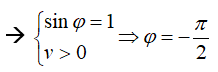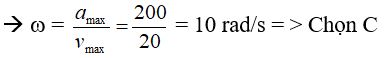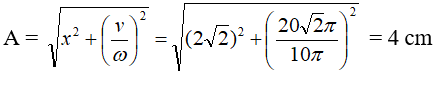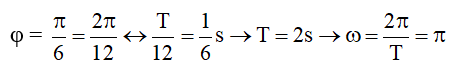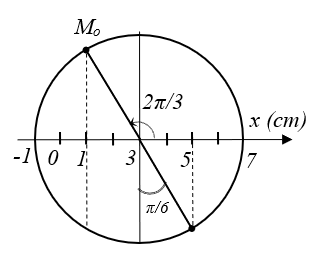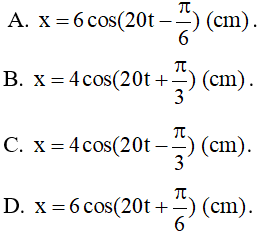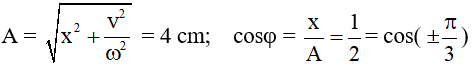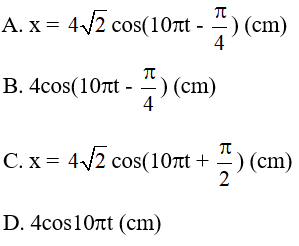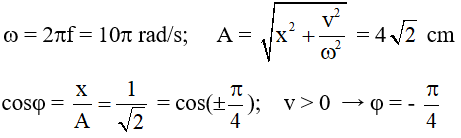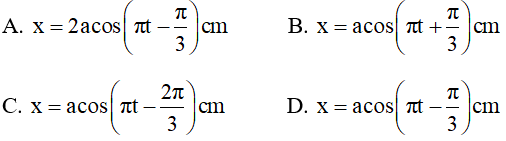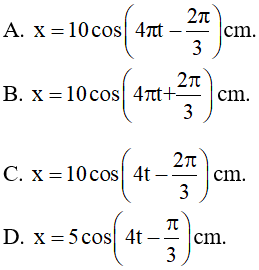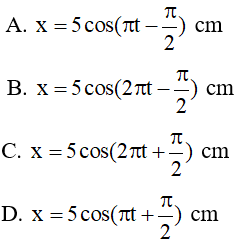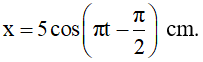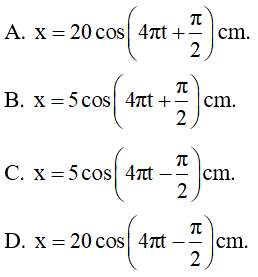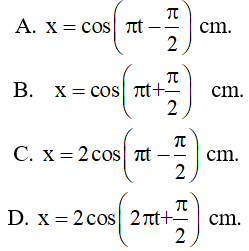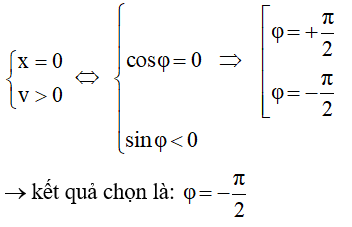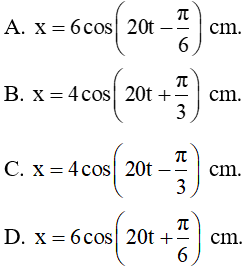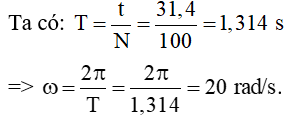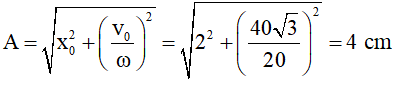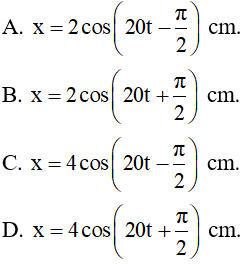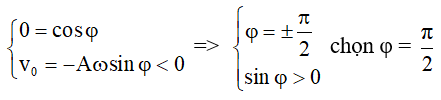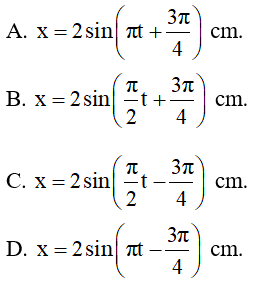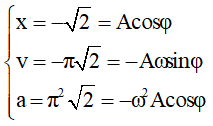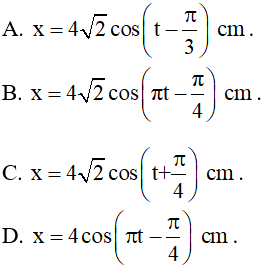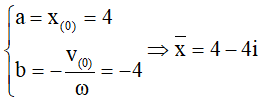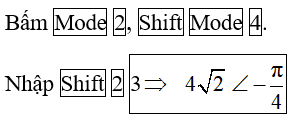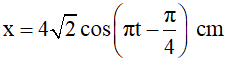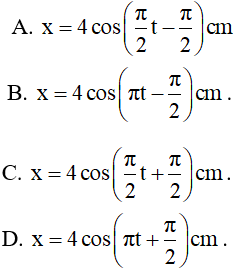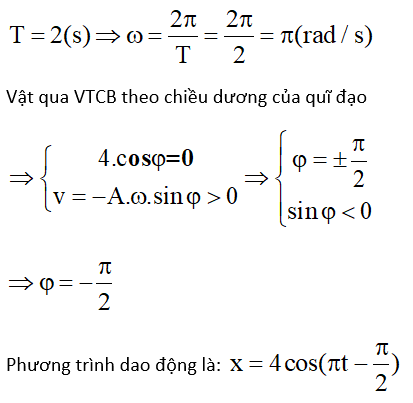Các dạng bài toán Viết phương trình dao động điều hòa (có đáp án 2024)

Các dạng bài toán Viết phương trình dao động điều hòa

Phần 1: Viết phương trình dao động của vật khi VTCB nằm tại gốc tọa độ

A. Phương pháp & Ví dụ

1. Phương pháp

- Tìm A:

Trong đó:

- L là chiều dài quỹ đạo của dao động

- S là quãng đường vật đi được trong một chu kỳ

- Tìm ω:

- Tìm φ

Cách 1: Dựa vào t = 0 ta có hệ sau:

(Lưu ý: v.φ < 0)

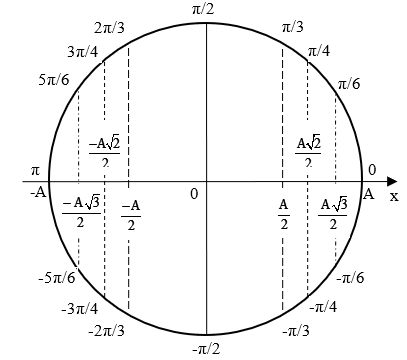
Cách 2: Sử dụng vòng tròn lượng giác (VLG)

Góc Φ là góc hợp bởi giữa trục Ox và OM tại thời điểm ban đầu.

Bước 3: Thay kết quả vào phương trình: x = Acos(ωt + Φ ) được phương trình dao động điều hòa của vật.

2. Ví dụ

Ví dụ 1: Một vật dao động điều hòa với biên độ A = 5cm, Trong 10 giây vật thực hiện được 20 dao động. Xác định phương trình dao động của vật biết rằng tại thời điểm ban đầu vật tại ví trí cân bằng theo chiều dương.

Lời giải:

Cách 1: Ta có: Phương trình dao động của vật có dạng: x = A.cos(ωt + φ) cm

Trong đó:

- A = 5 cm

- f = N/t = 20/10 = 2 Hz → ω = 2πf = 4π (rad/s).

- Tại t = 0 s vật đang ở vị trí cân bằng theo chiều dương

→ Phương trình dao động của vật là: x = 5cos(4πt - π/2)cm

Cách 2: Tìm φ:

- Tại t = 0 s vật đang ở vị trí cân bằng theo chiều dương (v > 0) → Φ < 0 → Chọn B

Ví dụ 2: Một vật dao động điều hòa trên quỹ đạo dài 6cm, Biết cứ 2s vật thực hiện được một dao động, tại thời điểm ban đầu vật đang ở vị trí biên dương. Xác định phương trình dao động của vật.

Lời giải:

Cách 1: Phương trình dao động của vật có dạng: x = A cos(ωt + φ) cm

Trong đó:

- A = L/2 = 3cm.

- T = 2 s

- ω = 2π/T = π (rad/s).

Tại t = 0s vật đang ở vị trí biên dương

Vậy phương trình dao động của vật là: x = 3cos(πt) cm

Cách 2: Tìm Φ:

- Tại t = 0s vật đang ở vị trí biên dương

⇒ Loại A, C còn lại B, D khác nhau biên độ A

- Tìm A = L/2 = 3cm

Ví dụ 3: Một vật dao động điều hòa với vận tốc khi đi qua vị trí cân bằng là v = 20cm/s. Khi vật đến vị trí biên thì có giá trị của gia tốc là a = 200 cm/s². Chọn gốc thời gian là lúc vận tốc của vật đạt giá trị cực đại theo chiều dương

Lời giải:

Cách 1: Phương trình dao động có dạng: x = A cos(ωt + φ) cm.

Trong đó:

- v_max = A.ω = 20 cm/s

- a_max = A.ω² = 200 cm/s²

- Tại t = 0 s vật có vận tốc cực đại theo chiều dương

Vậy phương trình dao động là: x = 2cos(10t - π/2 ) cm.

Cách 2: Tìm Φ

- Tại t = 0 s vật có vận tốc cực đại theo chiều dương (v > 0) ⇒ Φ < 0

⇒ Loại A, D còn lại B, C khác nhau ω

Ví dụ 4: Một vật dao động điều hòa với tần số góc 10π rad/s, tại thời điểm t = 0 vật đi qua vị trí có li độ x = 2√2π cm thì vận tốc của vật là 20√2 cm/s. Xác định phương trình dao động của vật?

Lời giải:

- Tại t = 0 s vật có vận tốc v = 20√2 π > 0 ⇒ Φ < 0

⇒ Loại B, C còn lại A, D khác nhau A

Phần 2: Viết phương trình dao động của vật có VTCB nằm ngoài gốc tọa độ

1. Phương pháp

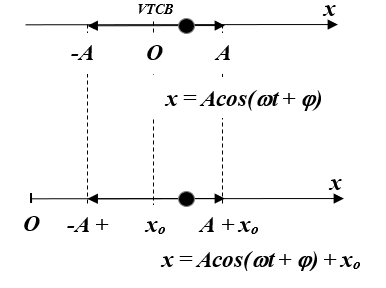
Nếu dịch chuyển trục Ox sao cho vị trí cân bằng có tọa độ x_o, khi đó biên dương là A + x, biên âm là –A + x_o. Áp dụng phép di chuyển trục tọa độ ta có:

Phương trình tọa độ của vật:

x = Acos( ωt + φ) + x_o

+ x là tọa độ của vật

+ Acos( ωt + φ) là li độ của vật

+ x_o là tọa độ của VTCB

2. Ví dụ

Ví dụ 1: Một chất điểm dao động điều hòa trên trục Ox, quỹ đạo của chất điểm nằm trong khoảng từ tọa độ -1 cm đến + 7 cm. Thời gian chất điểm đi từ tọa độ + 3 cm đến + 5 cm bằng 1/6 s. Thời điểm ban đầu, t = 0 được chọn lúc chất điểm đi qua vị trí tọa độ + 1 cm theo chiều âm. Phương trình dao động của chất điểm là

Lời giải:

Vẽ đường tròn mô tả dao động điều hòa từ –1cm đến 7 cm thì VTCB của vật có tọa độ x_o = + 3 cm.

Chất điểm đi từ 3 cm ⇒ 5cm: tương đương quay trên đường tròn góc

Vật đi từ -1 cm ⇒ + 7 cm nên độ dài quĩ đạo L = 8cm = 2A ⇒ A = 4cm.

Lúc t = 0, x = 1 cm theo chiều âm: dựng đường vuông góc với trục Ox tại 1cm và lấy điểm trên đường tròn. Suy ra, xác định được góc φ = 2π/3 rad.

⇒ Phương trình: x = Acos(ωt + φ) + x_o

x = 4cos(πt – 2π/3) + 3 cm.

B. Bài tập trắc nghiệm

Câu 1.(CĐ 2009). Chất điểm dao động điều hòa có phương trình vận tốc v = 4πcos2πt (cm/s). Gốc tọa độ ở vị trí cân bằng. Mốc thời gian được chọn vào lúc chất điểm có li độ và vận tốc là:

A. x = 2 cm, v = 0

B. x = 0, v = 4π cm/s

C. x = - 2 cm, v = 0

D. x = 0, v = - 4π cm/s

Lời giải:

Vì v = 4πcos2πt (cm/s) nên x = 2cos(2πt - π/2) cm;

cosφ = cos(-π/2) = = 0 → x = 0 → |v| = v_max; φ < 0 → v > 0. Đáp án B.

Câu 2. (CĐ 2010). Một chất điểm dao động điều hòa trên trục Ox có phương trình x = 8cos(πt + π/4) (cm). Gốc tọa độ ở vị trí cân bằng. Gốc thời gian (t = 0) được chọn lúc chất điểm có li độ và vận tốc là:

A. x = 4√2 cm và v = - 4π√2 cm/s

B. x = - 4√3 cm và v = 4π√3 cm/s

C. x = 4 cm và v = - 4π cm/s

D. x = 8 cm và v = 0

Lời giải:

cosφ = cos(π/4) = x/A = √2/2 → x = (√2/2)A = 4√2 cm

v = - 8πsin (π/4)= - 4π√2 cm/s. Đáp án A

Câu 3. (CĐ 2013). Một vật nhỏ dao động điều hòa dọc theo trục Ox (vị trí cân bằng ở O) với biên độ 4 cm và tần số 10 Hz. Tại thời điểm t = 0, vật có li độ 4 cm. Phương trình dao động của vật là:

A. x = 4cos(20πt + π) cm

B. x = 4cos20πt cm

C. x = 4cos(20πt – 0,5π) cm

D. x = 4cos(20πt + 0,5π) cm

Lời giải:

ω = 2πf = 20π rad/s; cosφ = x/A = 1 → φ = 0. Đáp án B

Câu 4.(ĐH 2011). Một chất điểm dao động điều hòa trên trục Ox. Trong thời gian 31,4 s chất điểm thực hiện được 100 dao động toàn phần. Gốc thời gian là lúc chất điểm đi qua vị trí có li độ 2 cm theo chiều âm với tốc độ là 40√3 cm/s. Lấy π = 3,14. Phương trình dao động của chất điểm là:

Lời giải:

T = 31,4/100 = 0,314 = 0,1π (s) rarr; ω = 2π/T = 20 rad/s.

v < 0 rarr; φ = π/3

Đáp án B

Câu 5. Vật dao động điều hòa với tần số f = 5 Hz. Khi t = 0, vật có li độ x = 4 cm và vân tốc v = 125,6 cm/s. Phương trình dao động của vật là:

Lời giải:

Đáp án A

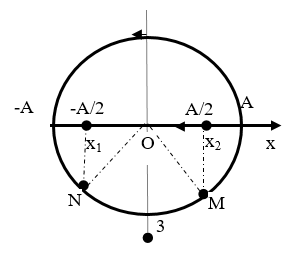
Câu 6. Một chất điểm dao động điều hòa theo phương nằm ngang trên đoạn MN = 2a. Thời gian ngắn nhất để nó đi từ M sang N là 1s. Tại thời điểm ban đầu chất điểm có li độ a/2 theo chiều dương. Phương trình dao động của chất điểm có dạng:

Lời giải:

Thời gian ngắn nhất để nó đi từ M sang N là 1s ⇒ T = 2s ⇒ ω = π rad/s

Tại thời điểm ban đầu chất điểm có li độ (a/2) : (a/2) = acosφ ⇒ φ = π/3 và φ = -π/3

Do chất điểm đi theo chiều dương ⇒ φ = -π/3

Phương trình dao động của chất điểm là: x = acos(πt - π/3)

Đáp án D

Câu 7. Một vật dao động điều hòa trên quỹ đạo dài 20cm. Sau (1/12)s kể từ thời điểm ban đầu vật đi được 10cm mà chưa đổi chiều chuyển động vật đến vị trí có li độ 5cm theo chiều dương. Viết phương trình dao động của vật.

Lời giải:

Ứng với thời gian vật từ N đến M với góc quay Δφ = φ/3

Hay thời gian đi là T/6 = 1/12

Suy ra T = (1/2)s , f = 2 Hz

Suy ra ω = 2πf = 4π rad/s.

Vật theo chiều dương nên: góc pha ban đầu dễ thấy là φ = -(2π/3)

Vậy phương trình dao động: Đáp án A.

Câu 8. Một vật nhỏ dao động điều hòa dọc theo trục Ox với biên độ 5 cm, chu kì 2 s. Tại thời điểm t = 0, vật đi qua cân bằng O theo chiều dương. Phương trình dao động của vật là:

Lời giải:

Ta có: A = 5cm; ω = 2π/T = π rad/s

Khi t = 0 vật đi qua cân bằng O theo chiều dương:

x = 0 và v > 0 ⇒ cosφ = 0 ⇒ φ = -π/2

Vậy phương trình dao động của vật là

Đáp án A.

Câu 9. Một chất điểm dao động điều hoà dọc theo trục Ox, quanh vị trí cân bằng O. Trong thời gian 20s vật thực hiện được 40 lần dao động. Tại thời điểm ban đầu vật chuyển động qua vị trí cân bằng theo chiều âm của trục toạ độ với vận tốc 20π cm/s. Phương trình dao động của vật là:

Lời giải:

Vật dao động điều hoà theo phương trình tổng quát x = Acos(ωt + φ), trong khoảng thời gian 20s vật thực hiện được 40 lần dao động suy ra chu kì dao động

T = 0,5s, tần số góc ω = 4π rad/s.

Tại thời điểm ban đầu t = 0 có x₀ = 0, v₀ = 20π cm/s. Vận tốc của vật khi vật chuyển động qua vị trí cân bằng là vận tốc cực đại v_max = ωA suy ra A = 5 cm

Tại thời điểm ban đầu vật chuyển động theo chiều âm của trục toạ độ nên φ = π/2

Vậy phương trình dao động của vật là 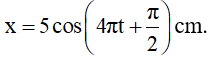Đáp án B.

Câu 10 Một vật dao động điều hòa với tần số f = 0,5 Hz, biên độ A = 2 cm.Viết phương trình dao động của vật. Chọn gốc thời gian khi vật đi qua vị trí cân bằng theo chiều dương.

Lời giải:

Phương trình dao động tổng quát là x = Acos(ωt + φ)

Với A = 2cm, ω = 2πf = π rad/s → phương trình dao động có dạng: x = 2cos(πt + φ)cm.

Tại thời điểm t = 0, ta có :

Phương trình dao động: x = 2cos(πt - π/2)cm.

Đáp án C

Câu 11. Một chất điểm dao động điều hòa trên trục Ox. Trong thời gian 31,4 s chất điểm thực hiện được 100 dao động toàn phần. Gốc thời gian là lúc chất điểm đi qua vị trí có li độ 2 cm theo chiều âm với tốc độ là 40√3 cm/s. Lấy π = 3,14. Phương trình dao động của chất điểm là:

Lời giải:

Áp dụng phương trình độc lập với thời gian ta có:

Từ điều kiện ban đầu tại t = 0 ta có x₀ = Acosφ = 2cm ; v₀ = – ωAsinφ < 0.

Nên cosφ = 1/2 ; sinφ > 0 đo đó φ = π/3

Vậy phương trình dao động của vật là x = 4cos(20t + π/3)cm.

Đáp án B

Câu 12. Một vật dao động điều hòa trên đoạn thẳng dài 4 cm với f = 10 Hz. Lúc t = 0 vật qua vị trí cân bằng theo chiều âm của quỹ đạo. Phương trình dao động của vật là :

Lời giải:

Cách giải 1: Ta có: ω = 2πf = 20π. Và A = MN/2 = 2 cm

Khi t = 0 : x₀ = 0, v₀ < 0 :

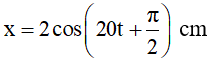
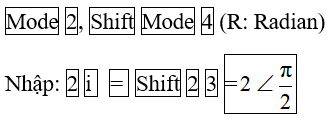
Vậy phương trình dao động của vật là Đáp án B.

Cách giải 2: Dùng Máy Fx 570Es bấm:

Vậy phương trình dao động của vật là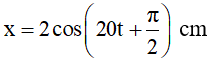 Đáp án B.

Câu 13. Một vật dao động điều hoà dọc theo trục Ox. Lúc vật qua vị trí có li độ x = -√2 cm thì có vận tốc v = -π√2 cm/s và gia tốc a = π²√2 cm/s². Chọn gốc toạ độ ở vị trí trên. Phương trình dao động của vật dưới dạng hàm số sin.

Lời giải:

Phương trình có dạng : x = Acos(ωt + φ)

Phương trình vận tốc : v = – Aωcos(ωt + φ)

Phương trình gia tốc : a = – Aω²cos(ωt + φ)

Khi t = 0 ; thay các giá trị x, v, a vào 3 phương trình đó ta có:

Lấy a chia cho x ta được: ω = π rad/s. Lấy v chia cho a ta được :

tanφ = -1 ⇒ φ = 3π/4 (vì cosφ < 0) ⇒ A = 2 cm

Vậy :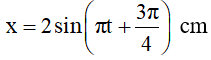Đáp án A.

Câu 14. Vật m dao động điều hòa với tần số 0,5 Hz, tại gốc thời gian nó có li độ x(0) = 4 cm, vận tốc v(0) = 12,56 cm/s, lấy π = 3,14. Hãy viết phương trình dao động.

Lời giải:

Tính ω = 2πf = 2π.0,5 = π rad/s

Khi t = 0

Vậy :

Đáp án B.

Câu 15. Vật dao động điều hòa với biên độ A = 4 cm và T = 2s. Chọn gốc thời gian là lúc vật qua VTCB theo chiều dương của quỹ đạo. Phương trình dao động của vật là:

Lời giải:

Đáp án B.

Câu 16. Một chất điểm dao động điều hòa theo phương trình: x = 20 + 10sin(10πt)cos(10πt). Tính li độ cực đại của chất điểm ?

A. 10 cm B. 5 cm C. 30 cm D. 10 cm

Lời giải:

Dùng công thức biến đổi tích thành tổng ta thu được phương trình:

Suy ra biên độ cực đại của dao động là A = 5 cm. Đáp án B.

Xem thêm các dạng bài tập và công thức Vật lí lớp 12 hay, chi tiết khác:

Các dạng bài toán tìm thời điểm vật qua vị trí x lần thứ n

Các dạng bài toán tìm li độ của vật tại thời điểm t

Các dạng bài toán tìm quãng đường, quãng đường lớn nhất, nhỏ nhất (smax, smin) vật đi được

Các dạng bài toán tính Tốc độ trung bình, vận tốc trung bình trong dao động điều hòa

Các dạng bài toán Phương pháp đường tròn hỗn hợp trong dao động điều hòa