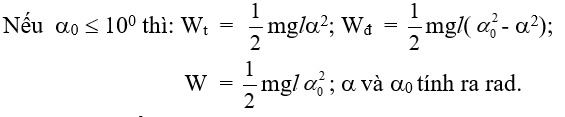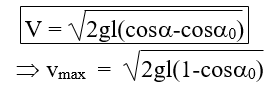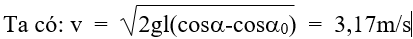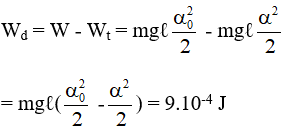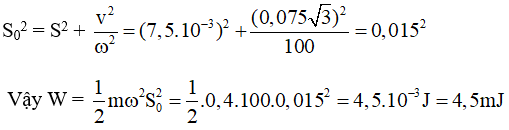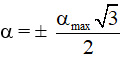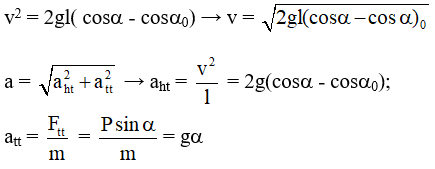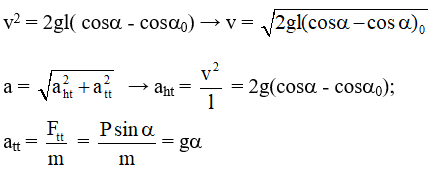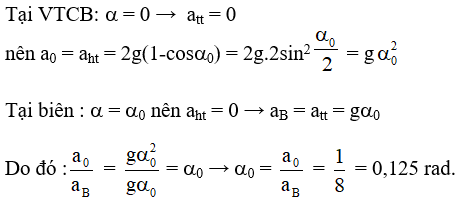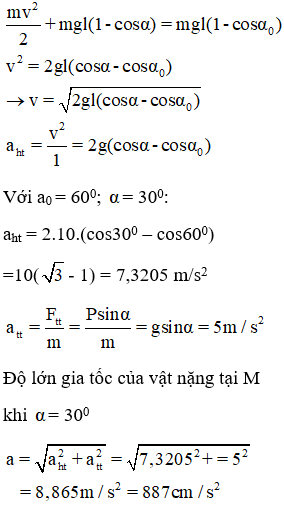Các dạng bài toán tìm năng lượng dao động, tìm lực căng dây của con lắc đơn (có đáp án 2024)

Các dạng bài toán tìm năng lượng dao động, tìm lực căng dây của con lắc đơn

A. Phương pháp & Ví dụ

1. Phương pháp

• Thế năng: W_t = mgh = mgl(1 - cosα).

• Động năng: W_đ = mv²/2 = mgl(cosα - cosα_o).

• Cơ năng: W = W_t + W_đ = mgl(1 - cosα_o).

♦ Vận tốc - lực căng dây

a) Vận tốc:

b) Lực căng dây:

T = mg (3cosα - 2cosα_o)

⇒ Tmax = mg(3 - 2cosα_o) Khi vật ngang qua vị trí cân bằng

⇒ Tmin = mg(cosα_o) Khi vật đạt vị trí biên

2. Ví dụ

Ví dụ 1: Một con lắc đơn có chiều dài l = 1m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45^ο và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác định cơ năng của vật?

A. 0,293J B. 0,3J C. 0,319J D. 0.5J

Lời giải:

♦ Ta có: W = W_tmax = mgl(1- cosα_o) = 0,1.10.1.(1- cos45^ο) = 0,293J

Ví dụ 2: Một con lắc đơn có chiều dài l = 1m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45^ο và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác định động năng của vật khi vật đi qua vị trí có α = 30^ο.

A. 0,293J B. 0,3J C. 0,159J D. 0.2J

Lời giải:

♦ Ta có: W_d = W - W_t = mgl(1- cosα_o) - mgl(1- cosα) = mgl(cosα - cosα_o)

= 0,1.10.1.(cos30^ο - cos45^ο) = 0,159 J.

Ví dụ 3: Một con lắc đơn có chiều dài l = 1m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 0,05rad và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác định cơ năng của vật?

A. 0,0125J B. 0,3J C. 0,319J D. 0.5J

Lời giải:

Ví dụ 4: Một con lắc đơn có chiều dài l = 1m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45^ο và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác định vận tốc của vật khi vật đi qua vị trí có α = 30^ο.

A. 3m/s B. 4,37m/s C. 3,25m/s D. 3,17m/s

Lời giải:

Ví dụ 5: Một con lắc đơn có chiều dài l = 1m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45^ο và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác lực căng dây của dây treo khi vật đi qua vị trí có α = 30^ο.

A. 2N B. 1,5N C. 1,18N D. 3,5N

Lời giải:

♦ Ta có: T = mg(3cosα - 2cosα_o) = 0,1.10(3.cosα = 30^ο - 2.cosα = 45^ο) = 1,18N.

B. Bài tập trắc nghiệm

Câu 1. Một con lắc đơn có chiều dài l = 1 m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1 kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45° và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác định cơ năng của vật?

A. 0,293 J B. 0,3 J C. 0,319 J D. 0.5 J

Lời giải:

Chọn A. Ta có: W = W_tmax = mgl(1- cosα₀) = 0,1.10.1.(1- cos45°) = 0,293J

Câu 2. Một con lắc đơn có chiều dài l = 1 m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1 kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45° và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác định động năng của vật khi vật đi qua vị trí có α = 30°.

A. 0,293 J B. 0,3 J C. 0,159 J D. 0.2 J

Lời giải:

Chọn C. Ta có: W_đ = W - W_t = mgl(1- cosα₀) - mgl(1- cosα) = mgl(cosα - cosα₀)

= 0,1.10.1.(cos30° - cos45°) = 0,159 J

Câu 3. Một con lắc đơn có chiều dài l = 1 m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1 kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45° và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác lực căng dây của dây treo khi vật đi qua vị trí có α = 30°.

A. 2 N B. 1,5 N C. 1,18 N D. 3,5 N

Lời giải:

Chọn C. Ta có: T = mg(3cosα - 2cosα₀) = 0,1.10(3.cos30° - 2.cos45°) = 1,18 N

Câu 4. Một con lắc đơn có chiều dài l = 1 m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1 kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 0,05 rad và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác định cơ năng của vật?

A. 0,0125 J B. 0,3 J C. 0,319 J D. 0.5 J

Lời giải:

Chọn A. Ta có: vì α nhỏ nên W_t = 0,5mglα₀² = 0,5.0,1.10.1 = 0,0125 J

Câu 5. Một con lắc đơn có chiều dài l = 1 m, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1 kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 0,05 rad và buông tay không vận tốc đầu cho vật dao động. Biết g = 10 m/s². Hãy xác định động năng của con lắc khi đi qua vị trí α = 0,04 rad.

A. 0,0125 J B. 9.10^-4 J C. 0,009 J D. 9.10⁴ J

Lời giải:

Chọn B

Câu 6. Một con lắc gồm quả cầu có khối lượng 400g và sợi dây treo không dãn có trọng lượng không đáng kể, chiều dài 0,1 (m) được treo thẳng đứng ở điểm A. Biết con lắc đơn dao động điều hòa, tại vị trí có li độ góc 0,075 (rad) thì có vận tốc 0,075√3 (m/s) Cho gia tốc trọng trường 10 (m/s² ). Cơ năng dao động của vật bằng

A. 4,7 mJ B. 4,4 mJ C 4,5 mJ D 4,8 mJ

Lời giải:

Ta có ω² = g/l = 10/0,1 = 100 và = αl = 0,075.0,1 = 7,5.10^-3 (m)

Vì vật dao động điều hòa nên:

Câu 7. Một con lắc đơn dao động điều hoà theo phương trình li độ góc α = 0,1cos(2πt + π/4) rad. Trong khoảng thời gian 5,25 s tính từ thời điểm con lắc bắt đầu dao động, có bao nhiêu lần con lắc có độ lớn vận tốc bằng 1/2 vận tốc cực đại của nó?

A. 11 lần B. 21 lần C. 20 lần D. 22 lần

Lời giải:

Trong một chu kì dao động có 4 lần v = v_max/2 tại vị trí W_đ = (1/4)W ⇒ W_t = (3/4) W_tmax tức là lúc li độ

Chu kì của con lắc đơn đã cho T = 2π/ω = 1 s.

Suy ra t = 5,25 s = 5T + T/4

Khi t = 0 : 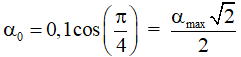vật chuyển động theo chiều âm về VTCB. Sau 5 chu kì vật trở lại vị trí ban đầu, sau T/4 tiếp vật chưa qua được vị trí α = -(α_max√3)/2

Do đó: Trong khoảng thời gian 5,25 s tính từ thời điểm con lắc bắt đầu dao động, con lắc có độ lớn vận tốc bằng 1/2 vận tốc cực đại của nó 20 lần. Chọn C.

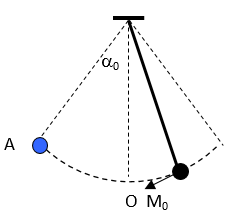
Câu 8. Treo một vật trong lượng 10 N vào một đầu sợi dây nhẹ, không co dãn rồi kéo vật khỏi phương thẳng đứng một góc α₀ và thả nhẹ cho vật dao động. Biết dây treo chỉ chịu được lực căng lớn nhất là 20 N. Để dây không bị đứt, góc α₀ không thể vượt quá:

A. 15° B. 30° C. 45° D. 60°.

Lời giải:

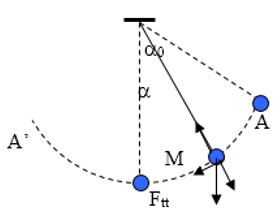
Xét thời điểm khi vật ở M, góc lệch của dây treo là α

Vận tốc của vật tại M: v² = 2gl( cosα - cosα₀)

Lực căng của dây treo khi vật ở M

T = mgcosα + (mv²)/l = mg(3cosα - 2cosα₀)

Khi α = 0: T_max = P(3 – 2cosα₀) = 10(3 – 2cosα₀) ≤ 20

→ 2cosα₀ ≥ 1 → cosα₀ ≥ 0,5 → α₀ ≤ 60°. Chọn D.

Câu 9. Một con lắc đơn gồm 1 vật nhỏ được treo vào đầu dưới của 1 sợi dây không dãn, đầu trên của sợi dây được buộc cố định. Bỏ qua ma sát của lực cản của không khí. Kéo con lắc lệch khỏi phương thẳng đứng một góc 0,1 rad rồi thả nhẹ. Tỉ số độ lớn gia tốc của vật tại VTCB và độ lớn gia tốc tại vị trí biên bằng:

A. 0,1 B. 0 C. 10 D. 1

Lời giải:

Xét thời điểm khi vật ở M, góc lệch của dây treo là α

Vận tốc của vật tại M:

Tại VTCB: α = 0 → a_tt = 0 nên a₀ = a_ht = 2g(1-cosα₀) = 2g.2sin²(α₀/2) = gα₀²

Tại biên : α = α₀ nên a_ht = 0 → a_B = a_tt = gα₀

Do đó : 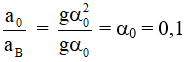. Chọn đáp án A

Câu 10. Một con lắc đơn dao động điều hòa với biên độ α₀ tại nơi có gia tốc trọng trường là g. Biết gia tốc của vật ở vị trí biên gấp 8 lần gia tốc của vật ở vị trí cân bằng. Giá trị α₀ là

A. 0,25 rad B. 0,375 rad

C. 0,125 rad D. 0,062 rad

Lời giải:

Xét thời điểm khi vật ở M, góc lệch của dây treo là α

Vận tốc của vật tại M:

Chọn C

Câu 11. Tại nơi có gia tốc trọng trường g = 10 m/s², một con lắc đơn có chiều dài 1 m, dao động với biên độ góc 60°. Trong quá trình dao động, cơ năng của con lắc được bảo toàn. Tại vị trí dây treo hợp với phương thẳng đứng góc 30°, gia tốc của vật nặng của con lắc có độ lớn là

A. 1232 cm/s² B. 500 cm/s²

C. 732 cm/s² D. 887 cm/s²

Lời giải:

Xét thời điểm khi vật ở M, góc lệch của dây treo là α

Vận tốc của vật tại M là v. Theo ĐL bảo toàn cơ năng:

Chọn D

Xem thêm các dạng bài tập và công thức Vật lí lớp 12 hay, chi tiết khác:

50 bài tập va chạm trong con lắc đơn, con lắc đơn đứt dây

50 bài tập Tổng hợp dao động điều hòa trong đề thi Đại học

Các dạng bài toán Tổng hợp dao động điều hòa

Các dạng bài toán tìm điều kiện để biên độ A, A1, A2 đạt cực đại, cực tiểu

Các dạng bài toán Dao động tắt dần là gì, dao động cưỡng bức, dao động duy trì