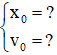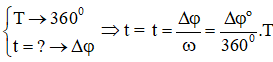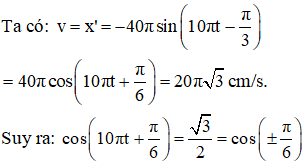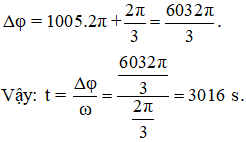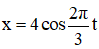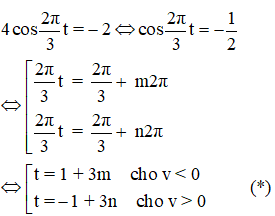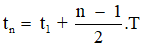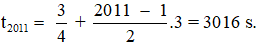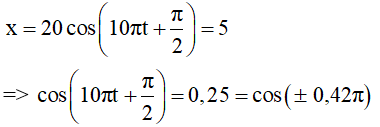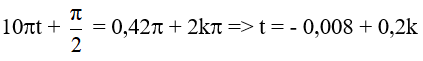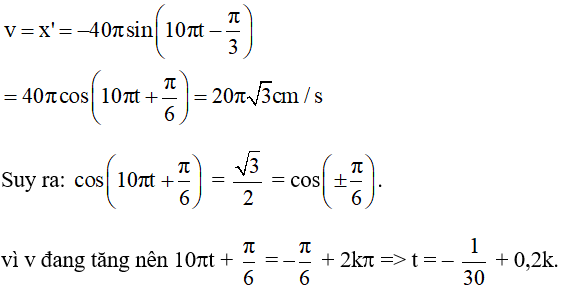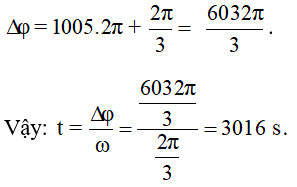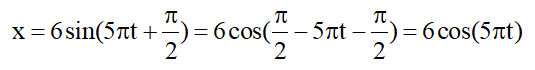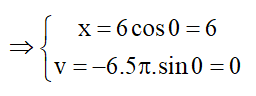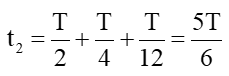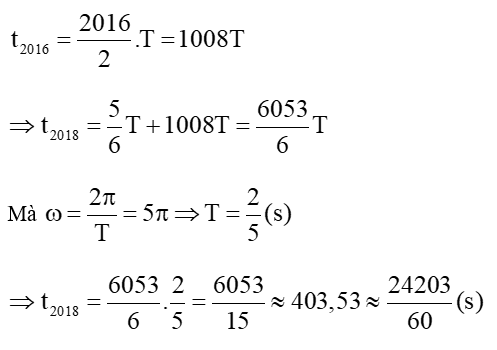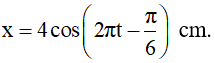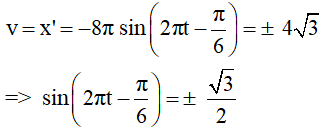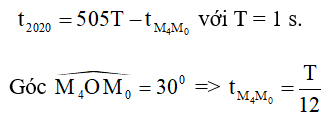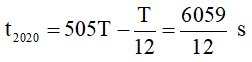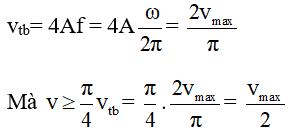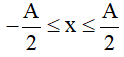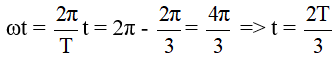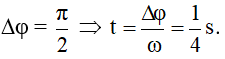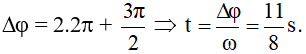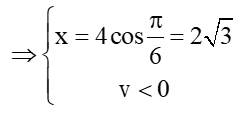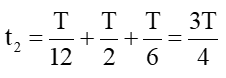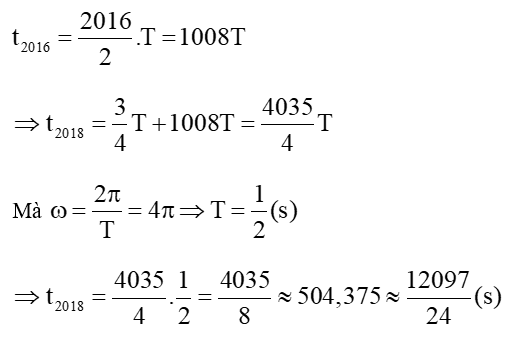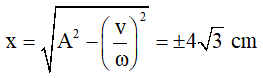Các dạng bài toán tìm thời điểm vật qua vị trí x lần thứ n (có đáp án 2024)

Các dạng bài toán tìm thời điểm vật qua vị trí x lần thứ n

A. Phương pháp & Ví dụ

1. Phương pháp

- Phương trình dao động có dạng: x = Acos(ωt + φ) cm.

- Phương trình vận tốc có dạng: v = -ωAsin(ωt + φ) cm/s.

Phương pháp chung:

a) Khi vật qua li độ x₁ thì:

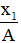
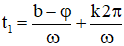
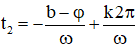
x₁ = Acos(ωt + φ) ⇒ cos(ωt + φ) = = cosb ⇒ ωt + φ = ±b + k2π

+ với k ∈ N khi b – φ > 0 (v < 0) vật qua x₀ theo chiều âm.

+ với k ∈ N* khi –b – φ < 0 (v > 0) vật qua x₀ theo chiều dương.

Kết hợp với điều kiện của bài toán ta loại bớt đi một nghiệm.

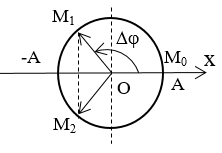
Lưu ý : Ta có thể dựa vào “ mối liên hệ giữa DĐĐH và CĐTĐ ”. Thông qua các bước sau:

• Bước 1: Vẽ đường tròn có bán kính R = A (biên độ) và trục Ox nằm ngang.

• Bước 2: – Xác định vị trí vật lúc t = 0 thì

- Xác định vị trí vật lúc t (x₁ đã biết)

• Bước 3: Xác định góc quét Δφ = = ?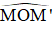

• Bước 4:

b) Khi vật đạt vận tốc v₁ thì:

Lưu ý:

+ Đề ra thường cho giá trị n nhỏ, còn nếu n lớn thì tìm quy luật để suy ra nghiệm thứ n.

+ Có thể giải bài toán bằng cách sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.

+ Dùng sơ đồ này có thể giải nhanh về thời gian chuyển động, quãng đường đi được trong thời gian Δt, quãng đường đi tối đa, tối thiểu….

+ Có thể áp dụng được cho dao động điện, dao động điện từ.

+ Khi áp dụng cần có kỹ năng biến đổi thời gian đề cho Δt liên hệ với chu kỳ T. và chú ý chúng đối xứng nhau qua gốc tọa độ.

2. Ví dụ :

Ví dụ 1: Một vật dao động điều hòa với phương trình 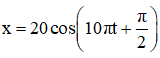cm. Xác định thời điểm đầu tiên vật đi qua vị trí có li độ x = 5 cm theo chiều ngược chiều với chiều dương kể từ thời điểm t = 0.

Lời giải:

Vì v < 0 nên ta chọn nghiệm:

10πt + π/2 = 0,42π + 2kπ → t = - 0,008 + 0,2k; với k ∈ Z.

Nghiệm dương nhỏ nhất trong họ nghiệm này (ứng với k = 1) là t = 0,192 s.

Chọn đáp án A

Ví dụ 2: Một vật dao động điều hòa với phương trình 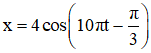cm. Xác định thời điểm gần nhất vận tốc của vật bằng 20π√3 cm/s và đang tăng kể từ lúc t = 0.

A. 1/6s B. 1/7s C. 1/8s D. 1/9s

Lời giải:

Vì v đang tăng nên: 10πt + π/6 = –π/6 + 2kπ → t = –1/30 + 0,2k.

Với k ∈ Z. Nghiệm dương nhỏ nhất trong họ nghiệm này là t = 1/6 s, ứng với k = 1.

Chọn đáp án A.

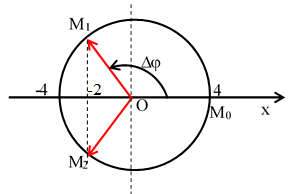
Ví dụ 3: Một chất điểm dao động điều hòa theo phương trình 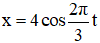(x tính bằng cm; t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = – 2 cm lần thứ 2011 tại thời điểm ?

A. 3015 s. B. 6030 s. C. 3016 s D. 6031 s.

Lời giải:

Cách 1: Từ phương trình 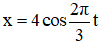ta nhận thấy lúc t = 0, x₀ = 4 cm, v₀ = 0. Vật qua x = – 2 là qua M₁ và M₂. Vật quay 1 vòng qua x = – 2 là 2 lần, qua lần thứ 2011 thì phải quay 1005 vòng (ứng với 2010 lần) rồi đi từ M0 đến M₁ để thêm 1 lần nữa là 2011 lần.

Khi đó, góc quét:

Vậy:

Chọn đáp án C

Cách 2: Giải phương trình lượng giác 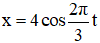. Theo đề bài ta có:

Từ (*) ta nhận thấy:

+ Lần thứ 1 ứng với m = 0.

+ Lần thứ 2 ứng với n = 1.

+ Lần thứ 3 ứng với m = 1.

……………………………

+ Lần thứ 2011 ứng với m = 1005.

Khi đó, ta có: t = 1 + 3m = 1 + 3.1005 = 3016 s.

Chọn đáp án C

Cách giải 3:

Ta nhận thấy vật đi qua vị trí có li độ x = - 2 cm lần thứ 2011 (n = 2011) nên n lẻ, khi đó ta có:

Với 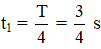là khoảng thời gian vật đi từ vị trí cân bằng đến vị trí x = - 2 lần thứ nhất.

Vậy:

Chọn đáp án C

Chú ý: Dạng bài toán tính thời điểm vật đi qua vị trí đã biết x (hoặc v, a, W_t, W_đ, F) lần thứ n ta có thể tính theo các công thức sau:

+ nếu n là lẻ. Với t₁ là khoảng thời gian vật đi từ vị trí cân bằng đến vị trí x lần thứ nhất.

+ nếu n là chẵn. Với t₂ là khoảng thời gian vật đi từ vị trí cân bằng đến vị trí x lần thứ hai.

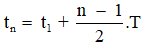
B. Bài tập trắc nghiệm

Câu 1. Một vật dao động điều hòa với phương trình

Xác định thời điểm đầu tiên vật đi qua vị trí có li độ x = 5 cm theo chiều ngược chiều với chiều dương kể từ thời điểm t = 0.

A. 0,192 s B. 1,023 s C. 0,063 s D. 0,963 s

Lời giải:

Ta có:

Vì v < 0 nên ta chọn nghiệm:

với k ∈ Z. Nghiệm dương nhỏ nhất trong họ nghiệm này (ứng với k = 1) là t = 0,192 s.

Đáp án A.

Câu 2. Một vật dao động điều hòa với phương trình 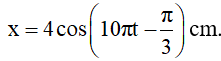Xác định thời điểm gần nhất vận tốc của vật bằng 20π√3 cm/s và đang tăng kể từ lúc t = 0.

A. 1/6 s B. 1/7 s C. 1/8 s D. 1/9 s

Lời giải:

Ta có:

Với k ∈ Z. Nghiệm dương nhỏ nhất trong họ nghiệm này là t = 1/6 s, ứng với k = 1.

Đáp án A.

Câu 3. Một chất điểm dao động điều hòa theo phương trình (x tính bằng cm; t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = – 2 cm lần thứ 2011 tại thời điểm ?

A. 3015 s B. 6030 s C. 3016 s D. 6031 s

Lời giải:

Từ phương trình 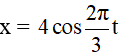ta nhận thấy lúc t = 0, x₀ = 4 cm, v_o = 0. Vật qua x = – 2 là qua M₁ và M₂. Vật quay 1 vòng qua x = – 2 là 2 lần, qua lần thứ 2011 thì phải quay 1005 vòng rồi đi từ M₀ đến M₁.

Khi đó, góc quét

Đáp án C

Câu 4. Một chất điểm dao động điều hòa theo phương trình 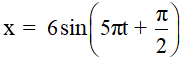(x tính bằng cm; t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = 3 cm lần thứ 2018 tại thời điểm?

Lời giải:

Tại t = 0 vật đang ở vị trí Biên vì

Ta nhận thấy vật đi qua vị trí có li độ x = 3 cm lần thứ 2018, với n = 2018 là số chẳn nên

t₂₀₁₈ = t₂ + t₂₀₁₆

Với t₂ là khoảng thời gian vật đi từ vị trí Biên đến vị trí x = 3 cm lần thứ hai,

Cứ 1 vòng thì vật đi qua vị trí x = 3cm 2 lần, nên:

Đáp án A.

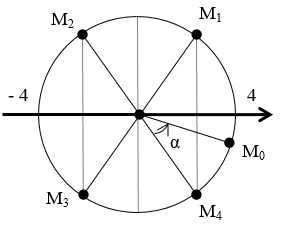
Câu 5. Một vật dao động với phương trình

Thời điểm vật có tốc độ 4π√3 cm/s lần thứ 2020 kể từ lúc dao động là:

Lời giải:

Ở bài này trong một chu kỳ có 4 lần vật có tốc độ 4π√3 cm/s.

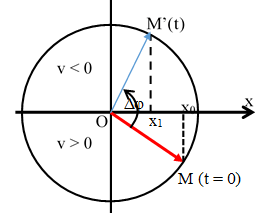
Khi t = 0 vật ở M₀x₀ = 2√3 cm, v₀ > 0. Ta có:

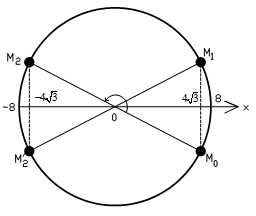
Trong một chu kì 4 lần vật có tốc độ 4π√3 cm/s ở các vị trí M_1.2.3.4

Lần thứ 2020 = 505.4 vật ở M₄:

Thời điểm vật có tốc độ 4π√3 cm/s lần thứ 2020 kể từ lúc dao động là:

Đáp án D

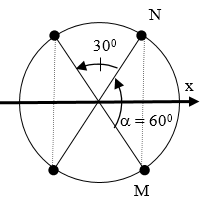
Câu 6. Một chất điểm dao động điều hòa với chu kì T. Gọi v_tb là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà v ≥ (π/4)v_tb là:

A. T/6 B. 2T/3 C. T/3 D. T/2

Lời giải:

Vận tốc trung bình trong một chu kì là:

tương ứng với li độ:

Vậy góc quay trong một chu kì mà khoảng thời gian v ≥ (π/4)v_tb là:

Đáp án B

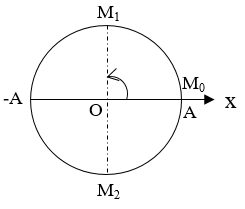
Câu 7. Một vật dao động điều hoà với phương trình x = 8cos2πt cm. Thời điểm thứ nhất vật đi qua vị trí cân bằng là:

A. 1/4 s B. 1/8 s C. 1/6 s D. 1/10 s

Lời giải:

Dùng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều. Vật đi qua VTCB, ứng với vật chuyển động tròn đều qua M₁ hoặc M₂.

Vì φ = 0, vật xuất phát từ M₀ nên thời điểm thứ nhất vật qua VTCB ứng với vật qua M₁.

Khi đó bán kính quét góc:

Đáp án A.

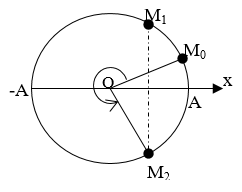
Câu 8. Một vật dao động điều hoà với phương trình 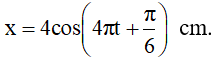Thời điểm thứ 3 vật qua vị trí x = 2 cm theo chiều dương.

A. 9/8 s B. 11/8 s C. 5/6 s D. 7/10 s

Lời giải:

Dùng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.Vật qua x = 2 theo chiều dương là qua M₂. Qua M₂ lần thứ 3 ứng với vật quay được 2 vòng (qua 2 lần) và lần cuối cùng đi từ M₀ đến M₂.

Góc quét

Đáp án B

Câu 9. Một vật dao động điều hoà với phương trình 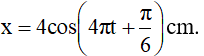Thời điểm thứ 2018 vật qua vị trí x = 2 cm.

Lời giải:

Tại t = 0 vật đang ở vị trí

Ta nhận thấy vật đi qua vị trí có li độ x = 2 cm lần thứ 2018, với n = 2018 là số chẳn nên

t₂₀₁₈ = t₂ + t₂₀₁₆

Với t₂ là khoảng thời gian vật đi từ vị trí x = 2√3 đến vị trí x = 2 cm lần thứ hai

Cứ 1 vòng thì vật đi qua vị trí x = 2cm 2 lần, nên:

Đáp án A.

Câu 10. Một vật dao động điều hoà với 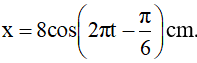Thời điểm thứ 2018 vật qua vị trí có v = - 8π cm/s.

A. 1008,5 s B. 1005 s C. 1012 s D. 1005,5 s

Lời giải:

Ta có

Vì v < 0 nên vật qua M₁ và M₂; Qua lần thứ 2018 thì phải quay 1008 vòng rồi đi từ M₀ đến M₂. Góc quét Δφ = 1008.2π + π

⇒ t = 1008,5 s.

Đáp án A

Xem thêm các dạng bài tập và công thức Vật lí lớp 12 hay, chi tiết khác:

Các dạng bài toán tìm li độ của vật tại thời điểm t

Các dạng bài toán tìm quãng đường, quãng đường lớn nhất, nhỏ nhất (smax, smin) vật đi được

Các dạng bài toán tính Tốc độ trung bình, vận tốc trung bình trong dao động điều hòa

Các dạng bài toán Phương pháp đường tròn hỗn hợp trong dao động điều hòa

Các dạng bài toán tìm thời gian ngắn nhất, lớn nhất vật đi qua li độ, vật có vận tốc, gia tốc