Nội dung bài viết

    Xem thêm

    Tính thể tích khối bát diện đều cạnh a

    Với giải bài tập 2 trang 25 sgk Toán lớp 12 Hình học được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

    1 3,457 21/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Bài 3: Khái niệm về thể tích của khối đa diện

    Bài 2 trang 25 Toán lớp 12 Hình học: Tính thể tích khối bát diện đều cạnh a.

    * Lời giải:

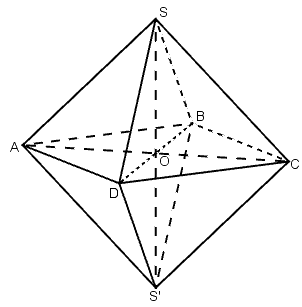
    Tính thể tích khối bát diện đều cạnh a (ảnh 1)

    Gọi khối bát diện đều là SABCDS’ cạnh a.

    * Ta chia khối bát diện thành hai khối chóp tứ giác đều bằng nhau là:

    S.ABCD và S’.ABCD có cạnh bằng a.

    Khi đó,

    VSABCDS’ = VS.ABCD + VS’.ABCD

    = 2.VS.ABCD

    Gọi O là giao điểm của AC và BD suy ra:

    SO ⊥ (ABCD)

    * Ta tính thể tính khối chóp tứ giác đều cạnh a.

    Tứ giác ABCD là hình vuông cạnh a nên có diện tích là:

    SABCD = a2

    Ta có:

    AC=AB2+BC2=a2+a2=a2

    ⇒AO=AC2=a22

    Áp dụng định lí Pytago vào tam giác SOA ta có:

    SO2=SA2−AO2=a2−a222=a22

    ⇒SO=a2

    Thể tích khối chóp tứ giác đều S.ABCD là:

    VS.ABCD=13SO.SABCD=13.a2.a2=a332

    Thể tích khối bát diện đều cạnh a là:

    VSABCDS'=2.VS.ABCD=2.a332=a323 (đvtt).

    * Phương pháp giải:

    - Áp dụng công thức tính thể tích khối chóp:

    Thể tích khối chóp.

    Thể tích khối chóp có diện tích đáy B và chiều cao h là: V=13B.h.

    * Lý thuyết cần nắm và dạng bài toán về thể tích khối đa diện:

    I. Khái niệm về thể tích của khối đa diện

    Người ta chứng minh được rằng: có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất V(H) thỏa mãn các tính chất sau:

    a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.

    b) Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2).

    c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì:

    V(H) = V(H1) + V(H2).

    Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Số đó cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).

    Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.

    - Định lí : Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.

    II. Thể tích của khối lăng trụ.

    Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h

    III. Thể tích khối chóp.

    Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là: V=13B.h.

    Xem thêm các bài viết liên quan hay, chi tiết:

    Lý thuyết Khái niệm về thể tích của khối đa diện (mới 2024 + Bài Tập) – Toán 12

    TOP 40 câu Trắc nghiệm Khái niệm về thể tích của khối đa diện (có đáp án 2024) - Toán 12

    Xem thêm lời giải bài tập Toán lớp 12 hay, chi tiết khác:

    Hoạt động 1 trang 22 Toán 12 Hình học: Có thể chia (H1) thành bao nhiêu khối lập phương bằng (H0)...

    Hoạt động 2 trang 22 Toán 12 Hình học: Có thể chia (H2) thành bao nhiêu khối hộp chữ nhật bằng (H1)...

    Hoạt động 3 trang 22 Toán 12 Hình học: Có thể chia (H) thành bao nhiêu khối hộp chữ nhật bằng (H2)...

    Hoạt động 4 trang 24 Toán 12 Hình học: Kim tự tháp Kê-ốp ở Ai Cập (h.1.27) được xây dựng vào khoảng 2500 năm trước Công nguyên...

    Bài 1 trang 25 Toán 12 Hình học: Tính thể tích khối tứ diện đều cạnh a...

    Bài 3 trang 25 Toán 12 Hình học: Cho hình hộp ABCD.A’B’C’D’...

    Bài 4 trang 25 Toán 12 Hình học: Cho khối chóp S.ABC...

    Bài 5 trang 26 Toán 12 Hình học: Cho tam giác ABC vuông cân ở A và AB = a...

    Bài 6 trang 26 Toán 12 Hình học: Cho hai đường thẳng chéo nhau d và d’...

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 3,457 21/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: