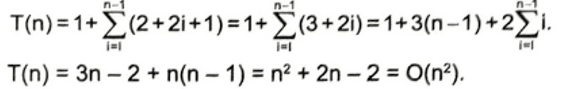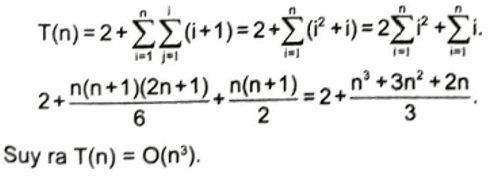Nội dung bài viết

    Xem thêm

    Sách bài tập Tin học 11 Bài 25 (Kết nối tri thức): Thực hành xác định độ phức tạp thời gian thuật toán

    Với giải sách bài tập Tin học 11 Bài 25: Thực hành xác định độ phức tạp thời gian thuật toán sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Tin học 11 Bài 25.

    1 365 15/01/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Tin học 11 Bài 25: Thực hành xác định độ phức tạp thời gian thuật toán

    Câu 25.1 trang 77 SBT Tin học 11: Tính độ phức tạp của các hàm thời gian sau:

    a) T(n) = n + 2log n.

    c) T(n) = 2100

    b) T(n) = n2 + 3nlogn + 2n.

    d) T(n) = 2n+1.

    Lời giải:

    a) T(n) = n + 2log n ≤ 3n với n ≥ 1. Vậy T(n) = O(n).

    b) T(n) = n2 + 3nlogn +2n ≤ 6n với n ≥ 1. Vậy T(n) = O(n).

    c) T(n) = O(1), độ phức tạp hằng số.

    d) T(n) = 2n+1 = 2.2" = O(2").

    Câu 25.2 trang 77 SBT Tin học 11: Cho biết thuật toán sau thực hiện công việc gì và hãy xác định độ phức tạp thời gian của thuật toán.

    1 def findMax(A):

    2 maxVal = A[0]

    Cho biết thuật toán sau thực hiện công việc gì và hãy xác định độ phức tạp

    Lời giải:

    Hàm trên thực hiện việc tìm phần tử lớn nhất của mảng A.

    Gọi n là kích thước của mảng, T(n) là thời gian thực hiện của thuật toán. Thời gian chạy của thuật toán được phân tích như sau:

    – Câu lệnh tại dòng 2 cần 1 đơn vị thời gian.

    – Vòng lặp for tại dòng 3 biến i chạy từ 1 đến n − 1, nên vòng lặp có n – 1 bước lặp.

    – Với mỗi bước lặp chương trình thực hiện 1 lệnh so sánh tại dòng 4 và 1 lệnh gán tại dòng 5 (nếu điều kiện thoả mãn).

    – Lệnh trả về tại dòng 6 cần 1 đơn vị thời gian.

    Tổng hợp lại chương trình trên có thời gian chạy là

    T(n) = 2 + 2(n-1) = 2n = O(n).

    Câu 25.3 trang 78 SBT Tin học 11: Cho biết hàm sau thực hiện công việc gì và hãy xác định độ phức tạp thời gian của chương trình.

    Cho biết hàm sau thực hiện công việc gì và hãy xác định độ phức tạp

    Lời giải:

    Hàm trên thực hiện in ra xâu đảo ngược của xâu đầu vào.

    Gọi n là kích thước của xâu đầu vào (số kí tự của xâu), T(n) là thời gian thực hiện

    của chương trình. Thời gian chạy của chương trình được phân tích như sau:

    – Câu lệnh tại dòng 2 và 3 cần 2 đơn vị thời gian.

    – Vòng lặp while thực hiện n lần lặp.

    – Với mỗi bước lặp chương trình thực hiện hai lệnh gán tại dòng 5 và 6.

    – Lệnh trả về tại dòng 7 cần 1 đơn vị thời gian.

    Tổng hợp lại chương trình trên có thời gian chạy là T(n) = 2 + 2n+1 = 2n + 3 = O(n).

    Câu 25.4 trang 78 SBT Tin học 11: Em hãy xác định thời gian chạy T(n) của thuật toán sắp xếp chèn sau, với n là độ dài của dãy A.

    Em hãy xác định thời gian chạy T(n) của thuật toán sắp xếp chèn sau

    Lời giải:

    Gọi n là kích thước của mảng, T(n) là thời gian thực hiện của thuật toán. Thời gian chạy của thuật toán được phân tích như sau:

    – Câu lệnh tại dòng 2 cần 1 đơn vị thời gian.

    – Vòng lặp for tại dòng 3 biến i chạy từ 1 đến n − 1, nên vòng lặp có n – 1 bước lặp.

    – Với mỗi bước lặp chương trình thực hiện:

    • Hai lệnh gán tại dòng 4 và 5.

    • Vòng lặp while tại dòng 6. Vòng lặp này sẽ chạy tối đa là i lần. Mỗi lần lặp chương trình sẽ thực hiện hai lệnh gán tại dòng 7 và 8, cần 2 đơn vị thời gian. • Lệnh gán tại dòng 9 cần 1 đơn vị thời gian.

    Tổng hợp lại chương trình trên có thời gian chạy tối đa là:

    Em hãy xác định thời gian chạy T(n) của thuật toán sắp xếp chèn sau

    Câu 25.5 trang 78 SBT Tin học 11: Xác định độ phức tạp thời gian của hàm sau:

    Xác định độ phức tạp thời gian của hàm sau:

    Lời giải:

    Gọi T(n) là thời gian thực hiện của chương trình. Thời gian chạy của chương trình được phân tích như sau:

    – Lệnh gán tại dòng 2 cần 1 đơn vị thời gian.

    – Vòng for tại dòng 3, biến i chạy từ 1 đến n, nên vòng lặp có n bước lặp.

    – Với mỗi bước lặp trên, chương trình thực hiện

    • Vòng lặp tại dòng 4, biến j chạy từ 1 đến i, nên vòng lặp thực hiện i bước lặp. • Với mỗi bước lặp:

    a Chương trình thực hiện vòng lặp tại dòng 5, biến k chạy từ j đến j + vòng lặp có i + 1 bước lặp.

    a Với mỗi bước lặp chương trình thực hiện 1 lệnh gán tại dòng 6 cần 1 đơn vị thời gian.

    – Lệnh trả về tại dòng 7 cần 1 đơn vị thời gian.

    Tổng hợp lại, hàm trên có thời gian chạy là:

    Xác định độ phức tạp thời gian của hàm sau:

    Câu 25.6 trang 78 SBT Tin học 11: Nếu f(n) = O(g(n)) thì có suy ra được g(n) = O(f(n)) hay không?

    Lời giải:

    Không. Ví dụ f(n) = n, g(n) = n2 thì rõ ràng f(n) = O(g(n)) nhưng ngược lại không đúng.

    Câu 25.7 trang 78 SBT Tin học 11: Giả sử f(n) = aknk + ak-1nk-1+....a1n +a0. Chứng minh rằng f(n) = O(nk).

    Lời giải:

    Theo Quy tắc 1, ta có O(f(n)) = O(aknk + ak-1nk-1+....a1n +a0)= O (nk)

    Vậy suy ra f(n) = O(nk)

    Xem thêm lời giải sách bài tập Tin học lớp 11 bộ sách Kết nối tri thức hay, chi tiết khác:

    Bài 26: Phương pháp làm mịn dần trong thiết kế chương trình

    Bài 27: Thực hành thiết kế chương trình theo phương pháp làm mịn dần

    Bài 28: Thiết kế chương trình theo mô đun

    Bài 29: Thực hành thiết kế chương trình theo mô đun

    Bài 30: Thiết lập thư viện cho chương trình

    Tham khảo các loạt bài Tin học 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 365 15/01/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: