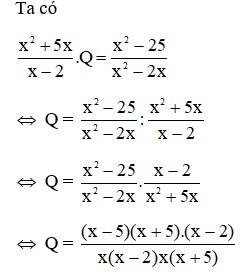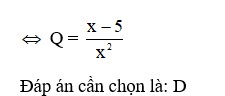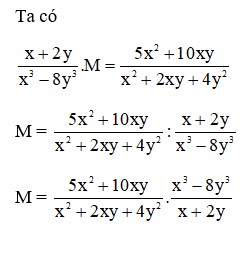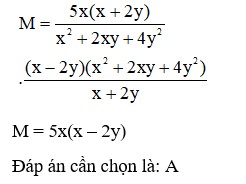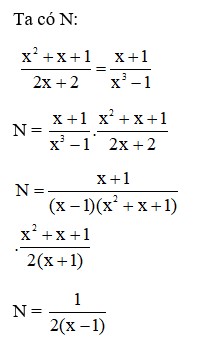Trắc nghiệm Phép nhân, phép chia các phân thức đại số có đáp án ( Vận dụng)
Trắc nghiệm Phép nhân, phép chia các phân thức đại số có đáp án ( Vận dụng)
-
305 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
16/07/2024Tìm biểu thức Q, biết 5xx2+2x+1.Q=xx2-1
 Xem đáp án
Xem đáp án
Ta có
Q = 5xx2+2x+1.Q=xx2-1
=> Q = xx2-1:5xx2+2x+1=xx2-1.x2+2x+15x
= x(x-1)(x+1).(x+1)25x=x+15(x-1)
Đáp án cần chọn là: D
Câu 4:
16/07/2024Tìm biểu thức M, biết
 Xem đáp án
Xem đáp án
Ta có
M =
M =
M =
M =
M =
M =
M =
Đáp án cần chọn là: B
Câu 8:
16/07/2024Cho x + y + z ≠ 0 và x = y + z. Chọn đáp án đúng
 Xem đáp án
Xem đáp án
Ta có
=
=
(vì x = y + z)
Đáp án cần chọn là: B
Câu 9:
16/07/2024Tính giá trị của biểu thức
T =
 Xem đáp án
Xem đáp án
Ta có x2 + (a – b)x – ab = x2 + ax – bx – ab
= x(x + a) – b(x + a) = (x – b)(x + a)
x2 – (a – b)x – ab = x2 – ax + bx – ab
= x(x – a) + b(x – a) = (x – a)(x + b)
x2 – (a + b)x + ab = x2 – ax – bx + ab
= x(x – a) – b(x – a) = (x – b)(x – a)
x2 + (a + b)x + ab = x2 + ax + bx + ab
= x(x + a) + b(x + a) = (x + a)(x + b)
x2 – (b – 1)x – b = x2 – bx + x – b
= x(x – b) + x – b = (x – b)(x + 1)
x2 + (b + 1)x + b = x2 + bx + x + b
= x(x + b) + x + b = (x + b)(x + 1)
x2 – (b + 1)x + b = x2 – bx – x + b
= x(x – b) – (x – b) = (x – b)(x – 1)
x2 – (1 – b)x – b = x2 – x + bx – b
= x(x – 1) + b(x – 1) = (x + b)(x – 1)
Khi đó
T=
=
=
Vậy T = 1
Đáp án cần chọn là: A
Câu 10:
23/07/2024Cho M = và N = . Khi x + y = 6, hãy so sánh M và N
 Xem đáp án
Xem đáp án
Ta có M =
=
=
= => M =
Và N =
=
=
=
N = (x + y)2
Với x + y = 6 thì M =
Và N = (x + y)2 = 62 = 36. Nên M < N
Đáp án cần chọn là: A
Câu 11:
16/07/2024Cho A = và B = . Khi x = 101, hãy so sánh A và B.
 Xem đáp án
Xem đáp án
Ta có
A=
=
=
=
Và
B =
=
=
=
=
=
Thay x = 101 vào A = ta được
A=
Thay x = 101 vào B = ta được
B=
Nhận thấy B = > 1; A = < 1 => B > A
Đáp án cần chọn là: B
Câu 12:
23/07/2024Rút gọn và tính giá trị biểu thức A = khi x = 994.
 Xem đáp án
Xem đáp án
Ta có A=
=
=
=
=
Thay x = 994 vào A = ta được A =
Đáp án cần chọn là: B
Câu 13:
23/07/2024Tính giá trị biểu thức C = khi x = 4; y =1; z = -2.
 Xem đáp án
Xem đáp án
Ta có C =
=
=
=
Vậy C =
Thay x = 4; y =1; z = -2 vào C = ta được C = = 6
Đáp án cần chọn là: A
Có thể bạn quan tâm
- Trắc nghiệm Phép chia các phân thức đại số (có đáp án) (305 lượt thi)
- Trắc nghiệm Phép nhân, phép chia các phân thức đại số có đáp án ( Thông hiểu) (268 lượt thi)
- Trắc nghiệm Phép nhân, phép chia các phân thức đại số có đáp án ( Vận dụng) (304 lượt thi)
Các bài thi hot trong chương
- Thi Online Trắc nghiệm Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức có đáp án (Vận dụng) (483 lượt thi)
- Trắc nghiệm Phép cộng các phân thức đại số (có đáp án) (461 lượt thi)
- Trắc nghiệm Phân thức đại số (có đáp án) (431 lượt thi)
- Trắc nghiệm Tính chất của phân thức đại số (có đáp án) (426 lượt thi)
- Trắc nghiệm Rút gọn phân thức (có đáp án) (425 lượt thi)
- Trắc nghiệm Toán 8: Rút gọn phân thức đại số có lời giải chi tiết (phần 1) (408 lượt thi)
- Trắc nghiệm Phép trừ các phân thức đại số (có đáp án) (403 lượt thi)
- Trắc nghiệm Phép nhân các phân thức đại số (có đáp án) (375 lượt thi)
- Trắc nghiệm Phân thức đại số.Tính chất cơ bản của phân thức có đáp án (Thông hiểu) (368 lượt thi)
- Trắc nghiệm Quy đồng mẫu thức nhiều phân thức (có đáp án) (351 lượt thi)