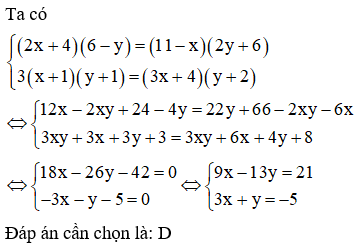21 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 9 Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số

Câu 1:

08/07/2024

Cho hệ phương trình $\{\begin{cases} 2 x + 3 y = - 2 \\ 3 x - 2 y = - 3 \end{cases}$ . Nghiệm của hệ phương trình là (x; y), tính x + y

A. x + y = −1

B. x + y = 1

C. x + y = 0

D. x + y = 2

Xem đáp án

\{\begin{cases} 2 x + 3 y = - 2 \\ 3 x - 2 y = - 3 \end{cases} \Leftrightarrow \{\begin{cases} 4 x + 6 y = - 4 \\ 9 x - 6 y = - 9 \end{cases} \Leftrightarrow \{\begin{cases} 13 x = - 13 \\ 2 x + 3 y = - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 0 \end{cases}

Vậy hệ đã cho có nghiệm duy nhất

(x; y) = (−1; 0)

$\Rightarrow$ x – y = −1 – 0 = −1

Đáp án cần chọn là: A

Câu 2:

20/07/2024

Cho hệ phương trình $\{\begin{cases} 8 x + 7 y = 16 \\ 8 x - 3 y = - 24 \end{cases}$ . Nghiệm của hệ phương trình là:

Xem đáp án

Ta có

$\{\begin{cases} 8 x + 7 y = 16 \\ 8 x - 3 y = - 24 \end{cases} \Leftrightarrow \{\begin{cases} 8 x + 7 y = 16 \\ 8 x + 7 y - (8 x - 3 y) = 16 - (- 24) \end{cases} \Leftrightarrow \{\begin{cases} 8 x + 7 y = 16 \\ 10 y = 40 \end{cases} \Leftrightarrow \{\begin{cases} y = 4 \\ 8 x + 7.4 = 16 \end{cases} \Leftrightarrow \{\begin{cases} y = 4 \\ x = - \frac{3}{2} \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất

(x; y) = $(- \frac{3}{2}; 4)$

Đáp án cần chọn là: A

Câu 3:

23/07/2024

Cho hệ phương trình $\{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 \\ x + y \sqrt{3} = \sqrt{2} \end{cases}$ . Biết nghiệm của hệ phương trình là (x; y), tính x + 3 $\sqrt{3}$ y

Xem đáp án

Ta có

$\{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 \\ x + y \sqrt{3} = \sqrt{2} \end{cases} \Leftrightarrow \{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 \\ x \sqrt{2} + y \sqrt{6} = 2 \end{cases} \Leftrightarrow \{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 \\ (\sqrt{6} + \sqrt{3}) y = 1 \end{cases} \Leftrightarrow \{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 \\ y = \frac{1}{\sqrt{6} + \sqrt{3}} \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{\sqrt{6} - \sqrt{3}}{3} \\ x \sqrt{2} - \sqrt{3} . \frac{\sqrt{6} - \sqrt{3}}{3} = 1 \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{\sqrt{6} - \sqrt{3}}{3} \\ x = 1 \end{cases}$

Vậy hệ đã cho có nghiệm duy nhất

(x; y) = $(1; \frac{\sqrt{6} - \sqrt{3}}{3})$

Đáp án cần chọn là: D

Câu 4:

23/07/2024

Cho hệ phương trình $\{\begin{cases} 2 x - 3 y = 1 \\ 4 x + y = 9 \end{cases}$

Nghiệm của hệ phương trình là (x; y), tính x – y:

A. x – y = −1

B. x – y = 1

C. x – y = 0

D. x – y = 2

Xem đáp án

Ta có:

$\{\begin{cases} 2 x - 3 y = 1 \\ 4 x + y = 9 \end{cases} \Leftrightarrow \{\begin{cases} 2 x - 3 y = 1 \\ 12 x + 3 y = 27 \end{cases} \Leftrightarrow \{\begin{cases} 2 x - 3 y = 1 \\ 2 x - 3 y + 12 x + 3 y = 1 + 27 \end{cases} \Leftrightarrow \{\begin{cases} 2 x - 3 y = 1 \\ 14 x = 28 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = 1 \end{cases}$

Vậy hệ đã cho có nghiệm duy nhất

(x; y) = (2; 1)

$\Rightarrow$ x – y = 2 – 1 = 1

Đáp án cần chọn là: B

Câu 5:

16/07/2024

Kết luận đúng về nghiệm của hệ phương trình $\{\begin{cases} \sqrt{x + 3} - 2 \sqrt{y + 1} = 2 \\ 2 \sqrt{x + 3} + \sqrt{y + 1} = 4 \end{cases}$

A. x. y = 1

B. x + y = 0

C. x – y = −2

D. y : x = 2

Xem đáp án

ĐK: x $\geq$ −3; y $\geq$ −1

Ta có:

$\{\begin{cases} \sqrt{x + 3} - 2 \sqrt{y + 1} = 2 \\ 2 \sqrt{x + 3} + \sqrt{y + 1} = 4 \end{cases} \Leftrightarrow \{\begin{cases} 2 \sqrt{x + 3} - 4 \sqrt{y + 1} = 4 \\ 2 \sqrt{x + 3} + \sqrt{y + 1} = 4 \end{cases} \Leftrightarrow \{\begin{cases} \sqrt{x + 3} - 2 \sqrt{y + 1} = 2 \\ - 5 \sqrt{y + 1} = 0 \end{cases} \Leftrightarrow \{\begin{cases} y = - 1 \\ \sqrt{x + 3} - 2. \sqrt{(- 1) + 1} = 2 \end{cases} \Leftrightarrow \{\begin{cases} y = - 1 \\ \sqrt{x + 3} = 2 \end{cases} \Leftrightarrow \{\begin{cases} y = - 1 \\ x + 3 = 4 \end{cases} \Leftrightarrow \{\begin{cases} y = - 1 \\ x = 1 \end{cases} (t m)$

Vậy hệ phương trình có nghiệm duy nhất

(x; y) = (1; −1)

Nên x + y = 1 + (−1) = 0

Đáp án cần chọn là: B

Câu 6:

14/07/2024

Cho hệ phương trình $\{\begin{cases} 4 \sqrt{x} - 3 \sqrt{y} = 4 \\ 2 \sqrt{x} + \sqrt{y} = 2 \end{cases}$ . Biết nghiệm của hệ phương trình là (x; y), tính x.y

A. 2

B. 0

C. −2

D. 1

Xem đáp án

ĐK: x $\geq$ 0; y $\geq$ 0

Ta có

$\{\begin{cases} 4 \sqrt{x} - 3 \sqrt{y} = 4 \\ 2 \sqrt{x} + \sqrt{y} = 2 \end{cases} \Leftrightarrow \{\begin{cases} 4 \sqrt{x} - 3 \sqrt{y} = 4 \\ 4 \sqrt{x} + 2 \sqrt{y} = 4 \end{cases} \Leftrightarrow \{\begin{cases} 5 \sqrt{y} = 0 \\ 2 \sqrt{x} + \sqrt{y} = 2 \end{cases} \Leftrightarrow \{\begin{cases} \sqrt{y} = 0 \\ 2 \sqrt{x} = 2 \end{cases} \Leftrightarrow \{\begin{cases} y = 0 \\ x = 1 \end{cases} (t m)$

Vậy hệ phương trình có 1 nghiệm duy nhất

(x; y) = (1; 0) $\Rightarrow$ x.y = 0

Đáp án cần chọn là: B

Câu 7:

16/07/2024

Cho hệ phương trình $\{\begin{cases} x + \frac{1}{y} = 2 \\ 2 x - \frac{3}{y} = 1 \end{cases}$ . Biết nghiệm của hệ phương trình là (x; y), tính $\frac{5 x}{y}$

Xem đáp án

ĐK: y $\neq$ 0

Ta có

$\{\begin{cases} x + \frac{1}{y} = 2 \\ 2 x - \frac{3}{y} = 1 \end{cases} \Leftrightarrow \{\begin{cases} 2 x + \frac{2}{y} = 4 \\ 2 x - \frac{3}{y} = 1 \end{cases} \Leftrightarrow \{\begin{cases} x + \frac{1}{y} = 2 \\ \frac{5}{y} = 3 \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{5}{3} \\ x + \frac{1}{\frac{5}{3}} = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{7}{5} \\ y = \frac{5}{3} \end{cases}$

Vậy hệ phương trình có 1 nghiệm duy nhất (x; y) = $(\frac{7}{5}; \frac{5}{3})$

Đáp án cần chọn là: B

Câu 8:

19/07/2024

Cho hệ phương trình $\{\begin{cases} 0, 3 \sqrt{x} + 0, 5 \sqrt{y} = 3 \\ 1, 5 \sqrt{x} - 2 \sqrt{y} = 1, 5 \end{cases}$ . Biết nghiệm của hệ phương trình là (x; y), tính x.y

A. 225

B. 0

C. 125

D. 15

Xem đáp án

ĐK: x $\geq$ 0; y $\geq$ 0

Nhân hai vế của phương trình thứ nhất với 5 rồi trừ từng vế của hai phương trình:

$\{\begin{cases} 0, 3 \sqrt{x} + 0, 5 \sqrt{y} = 3 \\ 1, 5 \sqrt{x} - 2 \sqrt{y} = 1, 5 \end{cases} \Leftrightarrow \{\begin{cases} 1, 5 \sqrt{x} + 2, 5 \sqrt{y} = 15 \\ 1, 5 \sqrt{x} - 2 \sqrt{y} = 1, 5 \end{cases} \Leftrightarrow \{\begin{cases} 4, 5 \sqrt{y} = 13, 5 \\ 1, 5 \sqrt{x} - 2 \sqrt{y} = 1, 5 \end{cases} \Leftrightarrow \{\begin{cases} \sqrt{y} = 3 \\ 1, 5 \sqrt{x} - 2 \sqrt{y} = 1, 5 \end{cases} \Leftrightarrow \{\begin{cases} \sqrt{y} = 3 \\ 1, 5 \sqrt{x} - 2.3 = 1, 5 \end{cases} \Leftrightarrow \{\begin{cases} y = 9 \\ 1, 5 \sqrt{x} = 7, 5 \end{cases} \Leftrightarrow \{\begin{cases} y = 9 \\ \sqrt{x} = 5 \end{cases} \Leftrightarrow \{\begin{cases} y = 9 \\ x = 25 \end{cases} (t m)$

Vậy hệ phương trình có nghiệm duy nhất

(x; y) = (25; 9) $\Rightarrow$ xy = 25.9=225

Đáp án cần chọn là: A

Câu 9:

20/07/2024

Cho hệ phương trình $\{\begin{cases} \frac{2}{x} + y = 3 \\ \frac{1}{x} - 2 y = 4 \end{cases}$ . Biết nghiệm của hệ phương trình là (x; y), tính $\frac{x}{y}$

A. 2

B. −2

C. $- \frac{1}{2}$

D. $\frac{1}{2}$

Xem đáp án

ĐK: x $\neq$ 0

Ta có

$\{\begin{cases} \frac{2}{x} + y = 3 \\ \frac{1}{x} - 2 y = 4 \end{cases} \Leftrightarrow \{\begin{cases} \frac{4}{x} + 2 y = 6 \\ \frac{1}{x} - 2 y = 4 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{2} \\ \frac{2}{x} + y = 3 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{2} \\ y = - 1 \end{cases} (t m)$

Vậy hệ phương trình cps 1 nghiệm duy nhất (x; y) = $(\frac{1}{2}; - 1)$

Đáp án cần chọn là: C

Câu 10:

17/07/2024

Tìm các giá trị của m để nghiệm của hệ phương trình $\{\begin{cases} \frac{x + 1}{4} - \frac{y}{2} = x + y + 1 \\ \frac{x - 2}{2} + \frac{y - 1}{3} = x + y - 1 \end{cases}$ cũng là nghiệm của phương trình (m + 2)x + 7my = m – 225

A. m = 40

B. m = 5

C. m = 50

D. m = 60

Xem đáp án

Ta có

$\{\begin{cases} \frac{x + 1}{4} - \frac{y}{2} = x + y + 1 \\ \frac{x - 2}{2} + \frac{y - 1}{3} = x + y - 1 \end{cases} \Leftrightarrow \{\begin{cases} x + 1 - 2 y = 4 x + 4 y + 4 \\ 3 x - 6 + 2 y - 2 = 6 x + 6 y - 6 \end{cases} \Leftrightarrow \{\begin{cases} 3 x + 6 y = - 3 \\ 3 x + 4 y = - 2 \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{- 1}{2} \\ x = 0 \end{cases}$

Thay x = 0; $y = - \frac{1}{2}$ vào phương trình

(m + 2)x + 7my = m – 225 ta được:

(m + 2).0 + 7m $(- \frac{1}{2})$ = m – 225

$\Leftrightarrow \frac{9}{2}$ m = 225 $\Leftrightarrow$ m = 50

Đáp án cần chọn là: C

Câu 11:

13/07/2024

Số nghiệm của hệ phương trình $\{\begin{cases} 5 (x + 2 y) - 3 (x - y) = 99 \\ x - 3 y = 7 x - 4 y - 17 \end{cases}$ là?

A. 2

B. Vô số

C. 1

D. 0

Xem đáp án

Ta có

$\{\begin{cases} 5 (x + 2 y) - 3 (x - y) = 99 \\ x - 3 y = 7 x - 4 y - 17 \end{cases} \Leftrightarrow \{\begin{cases} 5 x + 10 y - 3 x + 3 y = - 17 \\ x - 3 y - 7 x + 4 y = - 17 \end{cases} \Leftrightarrow \{\begin{cases} 6 x + 39 y = 297 \\ - 6 x + y = - 17 \end{cases} \Leftrightarrow \{\begin{cases} - 6 x + y = - 17 \\ 40 y = 280 \end{cases} \Leftrightarrow \{\begin{cases} 2 x + 13 y = 99 \\ - 6 x + y = - 17 \end{cases} \Leftrightarrow \{\begin{cases} y = 7 \\ x = 4 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất

(x; y) = (4; 7)

Đáp án cần chọn là: C

Câu 12:

21/07/2024

Kết luận nào đúng khi nói về nghiệm (x; y) của hệ phương trình $\{\begin{cases} \frac{x + y}{5} = \frac{x - y}{3} \\ \frac{x}{4} = \frac{y}{2} + 1 \end{cases}$

A. x > 0; y < 0

B. x < 0; y < 0

C. x < 0; y > 0

D. x > 0; y > 0

Xem đáp án

Ta có

$\{\begin{cases} \frac{x + y}{5} = \frac{x - y}{3} \\ \frac{x}{4} = \frac{y}{2} + 1 \end{cases} \Leftrightarrow \{\begin{cases} 3 x + 3 y = 5 x - 5 y \\ x = 2 y + 4 \end{cases} \Leftrightarrow \{\begin{cases} 2 x = 8 y \\ x = 2 y + 4 \end{cases} \Leftrightarrow \{\begin{cases} x = 4 y \\ x = 2 y + 4 \end{cases} \Leftrightarrow \{\begin{cases} x = 4 y \\ 2 y - 4 = 0 \end{cases} \Leftrightarrow \{\begin{cases} y = 2 \\ x = 8 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất

(x; y) = (2; 8)

Đáp án cần chọn là: D

Câu 13:

20/07/2024

Tìm a, b để hệ phương trình $\{\begin{cases} 4 a x + 2 b y = - 3 \\ 3 b x + a y = 8 \end{cases}$ có nghiệm là (2; −3)

A. a = 1; b = 11

B. a = −1; b = $\frac{11}{6}$

C. a = 1; b = − $\frac{11}{6}$

D. a = 1; b = $\frac{11}{6}$

Xem đáp án

Thay x = 2; y = −3 vào hệ phương trình ta được:

$\{\begin{cases} 4 a .2 + 2 b . (- 3) = - 3 \\ 3 b .2 + a (- 3) = 8 \end{cases} \Leftrightarrow \{\begin{cases} 8 a - 6 b = - 3 \\ - 3 a + 6 b = 8 \end{cases} \Leftrightarrow \{\begin{cases} 5 a = 5 \\ - 3 a + 6 b = 8 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ - 3.1 + 6 b = 8 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ 6 b = 11 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ b = \frac{11}{6} \end{cases}$

Vậy a = 1; b = $\frac{11}{6}$

Đáp án cần chọn là: D

Câu 14:

20/07/2024

Hệ phương trình $\{\begin{cases} (2 x + 4) (6 - y) = (11 - x) (2 y + 6) \\ 3 (x + 1) (y + 1) = (3 x + 4) (y + 2) \end{cases}$ tương đương với hệ phương trình nào dưới đây?

Xem đáp án

Câu 15:

21/07/2024

Tìm a, b biết đường thẳng d: y = ax + b đi qua hai điểm A (−4; −2); B (2; 1)

A. a = 0; b = $\frac{1}{2}$

B. a = $\frac{1}{2}$ ; b = 0

C. a = 1; b = 1

D. a = − $\frac{1}{2}$ ; b = $\frac{1}{2}$

Xem đáp án

Đường thẳng y = ax + b đi qua điểm

A (−4; −2) $\Leftrightarrow$ −4a + b = −2 (1)

Đường thẳng y = ax + b đi qua điểm

B (2; 1) $\Leftrightarrow$ 2a + b = 1 (2)

Từ (1) và (2) ta có hệ:

$\{\begin{cases} - 4 a + b = - 2 \\ 2 a + b = 1 \end{cases} \Leftrightarrow \{\begin{cases} - 6 a = - 3 \\ 2 a + b = 1 \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{2} \\ 2. \frac{1}{2} + b = 1 \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{2} \\ b = 0 \end{cases}$

Vậy a = $\frac{1}{2}$ ; b = 0

Đáp án cần chọn là: B

Câu 16:

22/07/2024

Cho hệ phương trình $\{\begin{cases} (m - 1) x + y = 2 \\ m x + y = m + 1 \end{cases}$ (m là tham số). Kết luận nào sau đây là đúng khi nói về nghiệm (x; y) của hệ phương trình?

A. Hệ phương trình luôn có nguyện duy nhất (x; y)thỏa mãn 2x + y ≤ 3

B. Hệ phương trình luôn có nguyện duy nhất (x; y)thỏa mãn 2x + y > 3

C. Hệ phương trình luôn có nguyện duy nhất (x; y)thỏa mãn 2x + y ≥ 3

D. Hệ phương trình luôn có nguyện duy nhất (x; y)thỏa mãn 2x + y = 3

Xem đáp án

Từ (m – 1) x + y = 2 thế vào phương trình còn lại ta được phương trình:

mx + 2 – (m – 1) x = m + 1

$\Leftrightarrow$ x = m – 1

suy ra y = 2 – (m – 1)² với mọi m

Vậy hệ phương trình luôn có nghiệm duy nhất

(x; y) = (m – 1; 2 – (m – 1)²)

2x + y = 2 (m – 1) + 2 – (m – 1)²

= −m² + 4m – 1

= 3 – (m – 2)² $\leq$ 3 với mọi m

Đáp án cần chọn là: A

Câu 17:

23/07/2024

Kết luận nào đúng khi nói về nghiệm (x; y) của hệ phương trình $\{\begin{cases} x + \frac{y}{2} = \frac{2 x - 3}{2} \\ \frac{x}{2} + 3 y = \frac{25 - 9 y}{8} \end{cases}$

A. x > 0; y < 0

B. x < 0; y < 0

C. x < 0; y > 0

D. x > 0; y > 0

Xem đáp án

Ta có

$\{\begin{cases} x + \frac{y}{2} = \frac{2 x - 3}{2} \\ \frac{x}{2} + 3 y = \frac{25 - 9 y}{8} \end{cases} \Leftrightarrow \{\begin{cases} 2 x + y = 2 x - 3 \\ 4 x + 24 y = 25 - 9 y \end{cases} \Leftrightarrow \{\begin{cases} y = - 3 \\ 4 x + 33 y = 25 \end{cases} \Leftrightarrow \{\begin{cases} x = 31 \\ y = - 3 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất

(x; y) = (31; −3) $\Rightarrow$ x > 0; y < 0

Đáp án cần chọn là: A

Câu 18:

22/07/2024

Tìm a, b để hệ phương trình $\{\begin{cases} 2 a x + b y = - 1 \\ b x - a y = 5 \end{cases}$ có nghiệm là (3; −4)

Xem đáp án

Thay x = 3; y = −4 vào hệ phương trình ta được

$\{\begin{cases} 2 a .3 + b (- 4) = - 1 \\ b .3 - a . (- 4) = 5 \end{cases} \Leftrightarrow \{\begin{cases} 6 a - 4 b = - 1 \\ 4 a + 3 b = 5 \end{cases} \Leftrightarrow \{\begin{cases} 12 a - 8 b = - 2 \\ 12 a + 9 b = 15 \end{cases} \Leftrightarrow \{\begin{cases} 17 b = 17 \\ 4 a + 3 b = 5 \end{cases} \Leftrightarrow \{\begin{cases} b = 1 \\ a = \frac{1}{2} \end{cases}$

Vậy a = $\frac{1}{2}$ ; b = 1

Đáp án cần chọn là: A

Câu 19:

23/07/2024

Nghiệm (x; y) của hệ phương trình $\{\begin{cases} \frac{7}{\sqrt{x} - 7} - \frac{4}{\sqrt{y} + 6} = \frac{5}{3} \\ \frac{5}{\sqrt{x} - 7} + \frac{3}{\sqrt{y} + 6} = 2 \frac{1}{6} \end{cases}$ có tính chất là:

A. x; y nguyên dương

B. x; y là số vô tỉ

C. x; y nguyên âm

D. x nguyên dương, y không âm

Xem đáp án

Điều kiện: x $\geq$ 0; x $\neq$ 7; y $\geq$ 0

Đặt $\frac{1}{\sqrt{x} - 7} = a; \frac{1}{\sqrt{y} + 6} = b$ ta được

$\{\begin{cases} 7 a - 4 b = \frac{5}{3} \\ 5 a + 3 b = 2 \frac{1}{6} \end{cases} \Leftrightarrow \{\begin{cases} 21 a - 12 b = 5 \\ 20 a + 12 b = \frac{26}{3} \end{cases}$

$\{\begin{cases} 21 a - 12 b = 5 \\ 41 a = \frac{41}{3} \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{3} \\ 21. \frac{1}{3} - 12 b = 5 \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{3} \\ b = \frac{1}{6} \end{cases}$

Trả lại biến ta có

$\{\begin{cases} \frac{1}{\sqrt{x} - 7} = \frac{1}{3} \\ \frac{1}{\sqrt{y} + 6} = \frac{1}{6} \end{cases} \Leftrightarrow \{\begin{cases} \sqrt{x} - 7 = 3 \\ \sqrt{y} + 6 = 6 \end{cases} \Leftrightarrow \{\begin{cases} x = 100 \\ y = 0 \end{cases} (t m)$

Vậy hệ phương trình có nghiệm

(x; y) = (100; 0)

Đáp án cần chọn là: D

Câu 20:

16/07/2024

Cho hệ phương trình $\{\begin{cases} 2 x + 3 y = \frac{7}{2} - m \\ 4 x - y = 5 m \end{cases}$ . Có bao nhiêu giá trị của m mà để hệ phương trình có nghiệm thỏa mãn: x² + 2y² = $\frac{25}{16}$

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Ta có

$\{\begin{cases} 2 x + 3 y = \frac{7}{2} - m \\ 4 x - y = 5 m \end{cases} \Leftrightarrow \{\begin{cases} 4 x + 6 y = 7 - 2 m \\ 4 x - y = 5 m \end{cases} \Leftrightarrow \{\begin{cases} 7 y = 7 - 7 m \\ 4 x - y = 5 m \end{cases} \Leftrightarrow \{\begin{cases} y = 1 - m \\ 4 x - (1 - m) = 5 m \end{cases} \Leftrightarrow \{\begin{cases} y = 1 - m \\ x = \frac{4 m + 1}{4} \end{cases}$

Thay vào x² + 2y² = $\frac{25}{16}$ ta có

$x^{2} + y^{2} = \frac{25}{16} \Leftrightarrow {(\frac{4 m + 1}{4})}^{2} + {(1 - m)}^{2} = \frac{25}{16}$

$\Leftrightarrow$ 16m² + 8m + 1 + 16m² – 32m + 16 = 25

$\Leftrightarrow$ 32m² – 24m – 8 = 0

$\Leftrightarrow$ 4m² − 3m – 1= 0

$\Leftrightarrow$ 4m² – 4m + m – 1= 0

$\Leftrightarrow$ (4m + 1)(m – 1) = 0

$\Leftrightarrow [\begin{array}{l} m = 1 \\ m = - \frac{1}{4} \end{array}$

Mà m > $\frac{1}{2} \Rightarrow$ m = 1 thỏa mãn

Vậy m = 1

Đáp án cần chọn là: B

Câu 21:

12/07/2024

Cho hệ phương trình: $\{\begin{cases} x - m y = m (1) \\ m x + y = 1 (2) \end{cases}$ (m là tham số). Kết luận nào sau đây là đúng khi nói về nghiệm (x; y) của hệ phương trình?

A. Hệ phương trình luôn có nghiệm duy nhất (x; y) thỏa mãn $x - y = \frac{m^{2} + 2 m + 1}{m^{2} + 1}$

B. Hệ phương trình luôn có nghiệm duy nhất (x; y) thỏa mãn $x - y = \frac{m^{2} + 2 m - 1}{m^{2} + 1}$

C. Hệ phương trình có vô số nghiệm với mọi m

D. Hệ phương trình vô nghiệm với mọi m

Xem đáp án

Từ phương trình (1): x – my = m x = m + my thế vào phương trình (2) ta được phương trình:

m (m + my) + y = 1

$\Leftrightarrow$ m² + m²y + y = 1

$\Leftrightarrow$ (m² + 1)y = 1 – m²

$\Leftrightarrow y = \frac{1 - m^{2}}{1 + m^{2}}$

(vì 1 + m² > 0; m)

suy ra x = m + m. $\frac{1 - m^{2}}{1 + m^{2}} = \frac{2 m}{1 + m^{2}}$ với mọi m

Vậy hệ phương trình luôn có nghiệm duy nhất

(x; y) = $(\frac{2 m}{1 + m^{2}}; \frac{1 - m^{2}}{1 + m^{2}})$

$\Rightarrow x - y = \frac{2 m}{1 + m^{2}} - \frac{1 - m^{2}}{1 + m^{2}} = \frac{m^{2} + 2 m - 1}{1 + m^{2}}$

Đáp án cần chọn là: B

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3