Trắc nghiệm Đường thẳng và mặt phẳng song song (có đáp án)
Trắc nghiệm Toán 11 Bài 3: Đường thẳng và mặt phẳng song song
-
1144 lượt thi
-
23 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
Chọn D.
Theo tính chất: Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
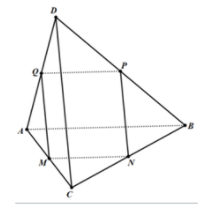
Gọi M là trung điểm của AC .
Ta có:
, N là trung điểm BC .
, P là trung điểm BD .
, Q là trung điểm AD.
Khi đó thiết diện là hình bình hành MNPQ.
Lại có: suy ra .
Vậy thiết diện cần tìm là hình thoi MNPQ .
Chọn C
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Chọn B.
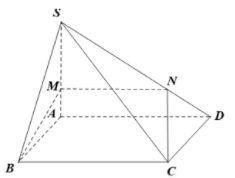
Ta có
Ta có nên và có giao tuyến song song AD
Trong , vẽ
Thiết diện của S.ABCD cắt bởi là tứ giác BCNM. Do (cùng song song AD) nên BCNM là hình thang.
Câu 4:
20/07/2024 Xem đáp án
Xem đáp án
Chọn C.
Câu 5:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án B.
Khi và đường thẳng thì ngoài trường hợp còn có trường hợp và chéo nhau.
Câu 6:
18/07/2024 Xem đáp án
Xem đáp án
Chọn D.
Cho qua không thẳng hàng.
Giả sử phân biệt là các đường thẳng nằm ngoài thỏa mãn
Trong trường hợp này
Nếu a và c đồng phẳng thì a cắt c
Nếu a và c không đồng phẳng thì a và c chéo nhau.
Câu 8:
21/07/2024 Xem đáp án
Xem đáp án
Chọn C.
Vị trí tương đối của đường thẳng và mặt phẳng là
• Đường thẳng nằm trong mặt phẳng.
• Đường thẳng song song với mặt phẳng.
• Đường thẳng cắt mặt phẳng.
Câu 9:
18/07/2024 Xem đáp án
Xem đáp án
Chọn B.
Theo định lý 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Câu 10:
21/07/2024 Xem đáp án
Xem đáp án
Chọn C.
Gọi là mp chứa a và song song b. có vtpt
Đồng thời qua A với
Do đó xác định duy nhất.
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Chọn C.
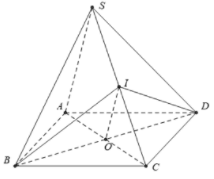
Ta có: nên A đúng.
Ta có: nên B đúng.
Ta có: cắt hình chóp theo thiết diện là tam giác nên Chọn C.
Ta có: nên D đúng.
Câu 12:
21/07/2024 Xem đáp án
Xem đáp án
Chọn D.
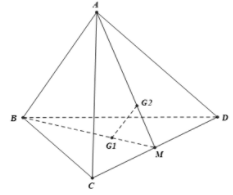
và lần lượt là trọng tâm các tam giác BCD và ACD nên , và CD đồng qui tại M (là trung điểm của CD ).
Vì nên và .
Lại có nên chọn đáp án D.
Câu 13:
23/07/2024 Xem đáp án
Xem đáp án
Chọn C.
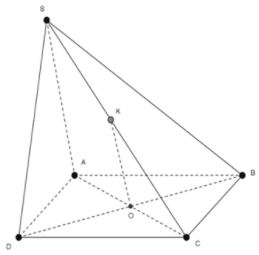
Gọi O là giao điểm của AC và BD. Do mặt phẳng qua BD nên
Trong tam giác SAC, kẻ OK song song SA
Do
Trong tam giác SAC ta có
là đường trung bình của
Vậy
Câu 14:
21/07/2024Cho tứ diện ABCD với M,N lần lượt là trọng tâm các tam giác ABD, ACD. Xét các khẳng định sau:
(I) .
(II) .
(III) .
(IV)) .
Các mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Chọn A.
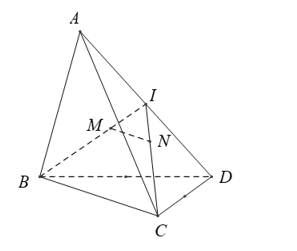
Gọi I là trung điểm của AD .
Do M,N là trọng tâm tam giác ABD , ACD nên
Theo định lý Talet có .
Mà .
Vậy .
Câu 15:
23/07/2024 Xem đáp án
Xem đáp án
Chọn B.
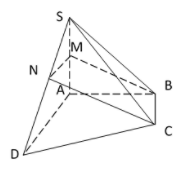
Sử dụng định lý ba đường giao tuyến ta có giao tuyến của với là MN sao cho
Ta có: nên thiết diện AMND là hình thang.
Lại có và M là trung điểm SA
là đường trung bình,
Vậy thiết diện MNCB là hình bình hành.
Câu 16:
21/07/2024 Xem đáp án
Xem đáp án
Chọn A.
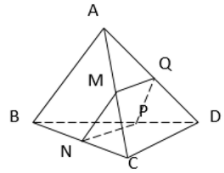
Trên kẻ
Trên kẻ
Ta có chính là mặt phẳng
Sử dụng đính lý ba giao tuyến ta có
với
Ta có:
thiết diện MNPQ là hình bình hành.
Câu 17:
23/07/2024Cho hình chóp S.ABCD với đáy ABCD là tứ giác lồi. Thiết diện của mặt phẳng tuỳ ý với hình chóp không thể là:
 Xem đáp án
Xem đáp án
Chọn A.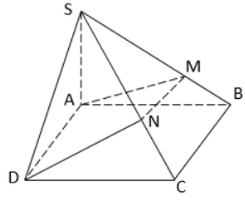
Thiết diện của mặt phẳng với hình chóp là đa giác được tạo bởi các giao tuyến của mặt phẳng đó với mỗi mặt của hình chóp.
Hai mặt phẳng bất kì có nhiều nhất một giao tuyến.
Hình chóp tứ giác S.ABCD có 5 mặt nên thiết diện của với S.ABCD có không qua 5 cạnh, không thể là hình lục giác 6 cạnh.
Sử dụng định lý ba đường giao tuyến ta có giao tuyến của với là MN sao cho
Ta có: nên thiết diện AMND là hình thang.
Câu 18:
22/07/2024 Xem đáp án
Xem đáp án
Chọn A.
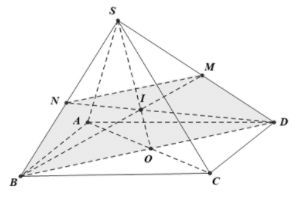
I trên đoạn SO và nên I là trọng tâm tam giác SBD. Suy ra M là trung điểm SD; N là trung điểm SB
Do đó và nên MNBD là hình thang.
Câu 19:
06/01/2025 Xem đáp án
Xem đáp án
Đáp án đúng là D.
Lời giải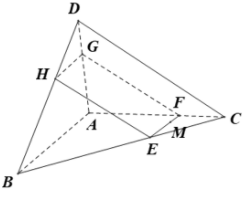
Ta có: nên giao tuyến và là đường thẳng song song AB
Trong Qua M vẽ Ta có
Tương tự trong qua E vẽ suy ra
Trong qua H vẽ suy ra
Thiết diện của ABCD cắt bởi là tứ giác EFGH
Ta có
Từ
là hình bình hành.
*Phương pháp giải:
Tứ giác có các cạnh đối song song là hình bình hành;
*Lý thuyết:
1. Định nghĩa
Hình bình hành là tứ giác có các cặp cạnh đối song song
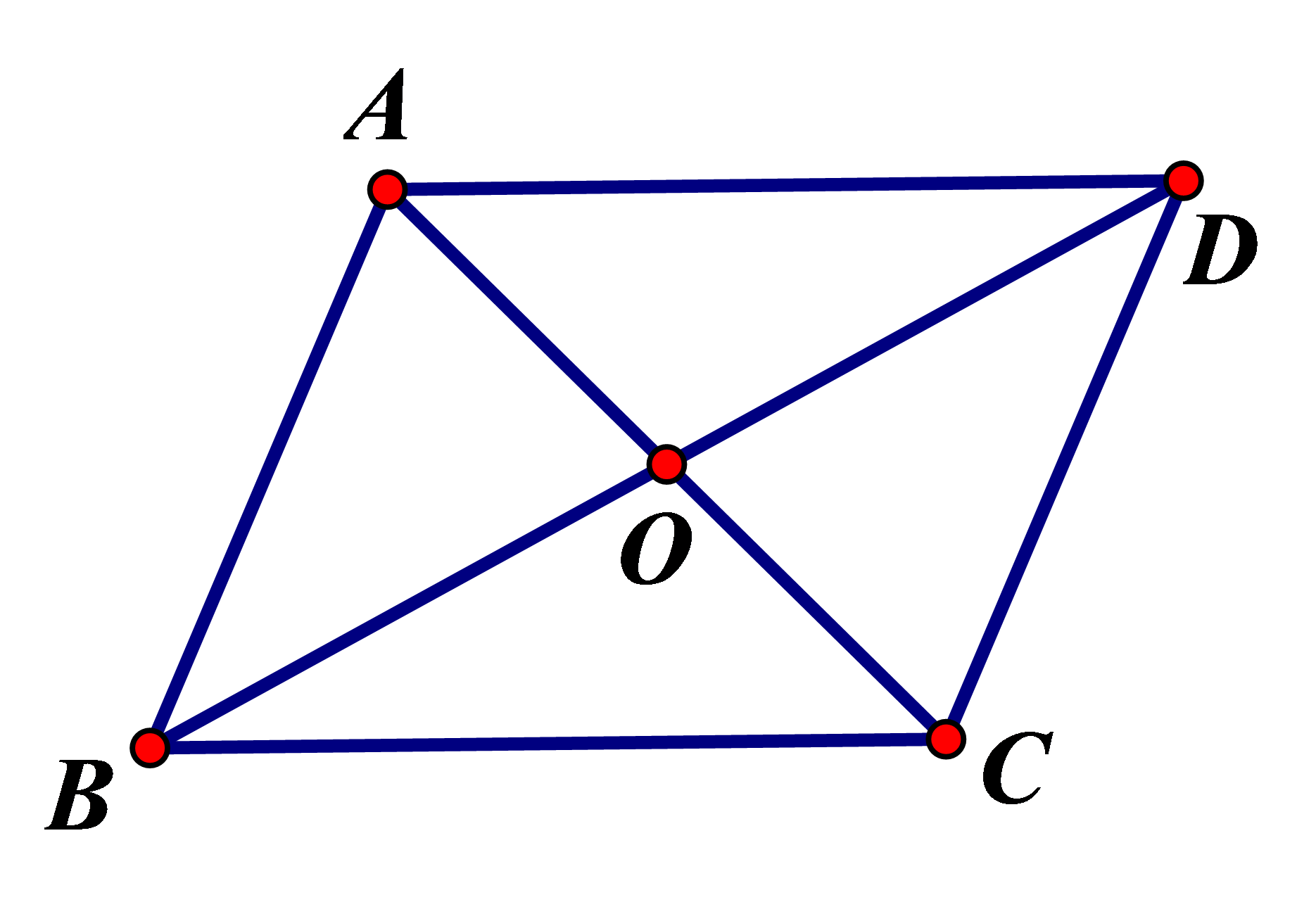
Tứ giác ABCD là hình bình hành
2. Tính chất: Trong hình bình hành
a) Các cạnh đối bằng nhau;
b) Các góc đối bằng nhau;
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
3. Dấu hiệu nhận biết
a) Tứ giác có các cạnh đối song song là hình bình hành;
b) Tứ giác có các cạnh đối bằng nhau là hình bình hành;
c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;
d) Tứ giác có các góc đối bằng nhau là hình bình hành;
e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành
Xem thêm
50 bài tập về hình bình hành (có đáp án ) – Toán 8Câu 20:
23/07/2024 Xem đáp án
Xem đáp án
Chọn A.
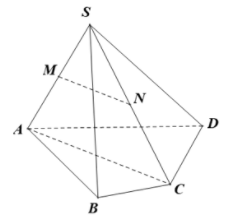
MN là đường trung bình của nên
Ta có
Câu 21:
23/07/2024 Xem đáp án
Xem đáp án
Chọn A.
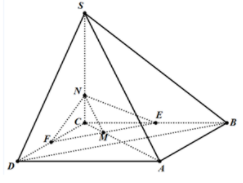
Ta có:
.
Lại có:
.
Vậy thiết diện cần tìm là tam giác NEF.
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
Chọn B.
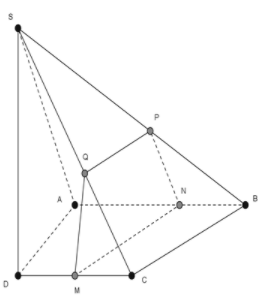
Trong mặt phẳng , qua M kẻ đường thẳng Khi đó,
Trong mặt phẳng , qua N kẻ đường thẳng Khi đó,
Vậy
Xét hai mặt phẳng và có
hai mặt phẳng cắt nhau theo một giao tuyến đi qua điểm P và song song với BC
Trong mặt phẳng kẻ Khi đó, PQ là giao tuyến của mặt phẳng với mặt phẳng . Vậy mặt phẳng cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ
Tứ giác MNPQ có
là hình bình hành. Từ đó suy ra
Trong tam giác SBC có P thuộc đoạn SB, Q thuộc đoạn SC và nên
Tứ giác MNPQ có
là hình thang có đáy lớn là MN
Câu 23:
18/07/2024 Xem đáp án
Xem đáp án
Chọn A.
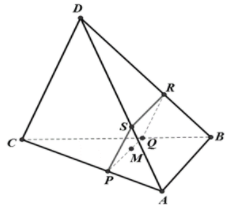
Ta có:
Từ ta được thiết diện cần tìm là hình bình hành PQRS.
Có thể bạn quan tâm
- Trắc nghiệm Đường thẳng và mặt phẳng song song (có đáp án) (1143 lượt thi)
- Trắc nghiệm Đường thẳng song song với mặt phẳng có đáp án (392 lượt thi)
- Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án (Nhận biết) (407 lượt thi)
- Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án (Thông hiểu) (366 lượt thi)
- Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án (Vận dụng) (346 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1) (1389 lượt thi)
- 100 câu trắc nghiệm Đường thẳng, Mặt phẳng trong không gian nâng cao (phần 1) (1222 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song (có đáp án) (992 lượt thi)
- Trắc nghiệm Hai mặt phẳng song song (có đáp án) (748 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án) (562 lượt thi)
- Trắc nghiệm Phép chiếu song song. Hình biểu diễn của một hình không gian (có đáp án) (544 lượt thi)
- Trắc nghiệm Ôn chương 2 - hình học (có đáp án) (533 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (516 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (Vận dụng) (415 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (408 lượt thi)