50 câu hỏi trắc nghiệm thuộc Đề thi thử tốt nghiệp môn Toán THPT năm 2022 có đáp án (Đề 6)

Hình hộp chữ nhật đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?

A. 2

B. 1

C. 3

D. 4

Xem đáp án

Đáp án C

Có 3 mặt phẳng đối xứng như trong hình vẽ sau:

Câu 2:

Cho số phức z = (1-2i)². Tính mô đun của số phức $\frac{1}{z}$

A. $\frac{1}{5}$

B. $\sqrt{5}$

C. $\frac{1}{25}$

D. $\frac{1}{\sqrt{5}}$

Xem đáp án

Câu 3:

15/07/2024

Tìm tất cả các giá trị của tham số m để phương trình $x^{3} + 3 x^{2} - 2 = m$ có hai nghiệm phân biệt.

A. $m \in (- \infty; - 2] .$

B. $m \notin [- 2; 2] .$

C. $m \in [2; + \infty) .$

D. $m \in \{- 2; 2\} .$

Xem đáp án

Câu 4:

Trên đồ thị $(C) : y = \frac{x + 1}{x + 2}$ có bao nhiêu điểm M mà tiếp tuyến với (C) tại M song song với đường thẳng $d : x + y = 1.$

A. 0

B. 4

C. 3

D. 2

Xem đáp án

Câu 5:

Cho hàm số $y = x^{3} + b x^{2} + c x + d, (b, c, d \in ℝ)$ có đồ thị như hình vẽ. Mệnh đề nào dưới đây là đúng?

A. $b < 0, c < 0, d > 0.$

B. $b > 0, c < 0, d > 0.$

C. $b < 0, c > 0, d < 0.$

D. $b > 0, c > 0, d > 0.$

Xem đáp án

Câu 6:

14/07/2024

Cho hàm số y = f(x) có $f' (x) > 0 \forall x \in ℝ$ . Tìm tập hợp tất cả các giá trị thực của x để $f (\frac{1}{x}) < f (1) .$

A. $(- \infty; 0) \cup (0; 1) .$

B. $(- \infty; 0) \cup (1; + \infty) .$

C. $(- \infty; 1) .$

D. $(0; 1) .$

Xem đáp án

Câu 7:

Cho hàm số y = f(x) có đạo hàm $y' = x^{2} (x - 2)$ . Mệnh đề nào sau đây đúng?

A. Hàm số nghịch biến trên R

B. Hàm số đồng biến trên (0;2)

C. Hàm số nghịch biến trên (-∞;0) và (2;+∞)

D. Hàm số đồng biến trên (2;+∞)

Xem đáp án

Câu 8:

Cho cấp số nhân (u_n) có u₁ = 2 và biểu thức 20u₁-10u₂+u₃ đạt giá trị nhỏ nhất. Tìm số hạng thứ bảy của cấp số nhân (u_n) ?

A. 2000000.

B. 136250.

C. 39062.

D. 31250.

Xem đáp án

Câu 9:

Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm B(2;1;-3) đồng thời vuông góc với hai mặt phẳng $(Q) : x + y + 3 z = 0, (R) : 2 x - y + z = 0$ là:

A. $4 x + 5 y - 3 z + 22 = 0.$

B. $4 x + 5 y - 3 z + 22 = 0.$

C. $2 x + y - 3 z - 14 = 0.$

D. $4 x + 5 y - 3 z - 22 = 0.$

Xem đáp án

Câu 10:

Đạo hàm của hàm số y = ln(5-3x²) là:

A. $\frac{6}{3 x^{2} - 5} .$

B. $\frac{2 x}{5 - 3 x^{2}} .$

C. $\frac{6 x}{3 x^{2} - 5} .$

D. $\frac{- 6 x}{3 x^{2} - 5} .$

Xem đáp án

Câu 11:

Lý thuyết Số phức (mới 2024 + Bài Tập) – Toán 12

Đặt a = log₂5 và a = log₃5. Biểu diễn đúng log₆5 theo a, b là:

A. $\frac{1}{a + b} .$

B. $a + b .$

C. $\frac{a b}{a + b} .$

D. $\frac{a + b}{a b} .$

Xem đáp án

Câu 12:

05/12/2024

Cho số phức z thỏa mãn $2 z - i . \bar{z} = 2 + 5 i .$ Môđun của số phức z bằng

A. $|z| = 7.$

B. $|z| = 5.$

C. $|z| = 25.$

D. $|z| = \frac{\sqrt{145}}{5} .$

Xem đáp án

Đáp án đúng: B

*Lời giải:

*Phương pháp giải:

Áp dụng công thức tính modun số phức để tính

*Lý thuyến cần nắm và các dạng bài toán về

1. Số i.

Số i là số thỏa mãn: i2 = –1.

2. Định nghĩa số phức

Mỗi biểu thức dạng a + bi , trong đó $a; b \in R$ ; i2 = –1 được gọi là một số phức.

Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.

Tập hợp các số phức kí hiệu là C.

3. Số phức bằng nhau

– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :

a + bi = c + di a = c và b = d.

– Chú ý :

a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.

Như vậy, mỗi số thực cũng là một số phức. Ta có : $R \subset C$ .

b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi

Đặc biệt : i = 0 + 1.i

Số i được gọi là đơn vị ảo.

4. Biểu diễn hình học số phức

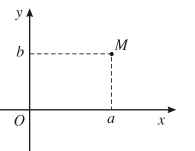
Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.

5. Mô đun của số phức.

Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.

Độ dài của vecto $\vec{O M}$ được gọi là môđun của số phức z và kí hiệu là |z|.

Vậy $|z| = |\vec{O M}|$ hay $|a + b i| = |\vec{O M}|$ .

Ta thấy: $|a + b i| = \sqrt{a^{2} + b^{2}}$

6. Số phức liên hợp

– Định nghĩa : Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hợp của z và kí hiệu là $\bar{z} = a - b i$ .

– Nhận xét :

+ Trên mặt phẳng tọa độ các điểm biểu diễn z và $\bar{z}$ đối xứng nhau qua trục Ox. $|a + b i| = \sqrt{a^{2} + b^{2}}$

+ Từ định nghĩa ta có: $\bar{\bar{z}} = z; |\bar{z}| = |z|$ .

Các dạng bài tập số phức và cách giải

Dạng 1: Các dạng quỹ tích đơn giản căn bản

Đường thẳng: Quỹ tích các điểm M biểu diễn số phức z = x +yi là đường thẳng nếu như M (x;y) có tọa độ thỏa mãn phương trình đường thẳng: Ãx +By + C = 0

Đường tròn: QUỹ tích các điểm M biểu diễn số phức z = x + yi là đường tròn nếu như M(x; y) có tọa độ thỏa mãn phương trình đường tròn (C) : (x - a)2 + (b -y)2 = R2. Trong đó thì I (a; b) là tâm đường trong và R là bán kính đường tròn.

Đường elip: quỹ tích các điểm M biểu diễn số phức z = x +yi là đường elip nếu như M(x; y) có tọa độ thỏa mãn phương trình đường elip (E): $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ = 1 trong đó thì a,b tương ứng với các bán trục lớn và bán trục nhỏ của elip

Dạng 2: Các dạng bài tập tìm phần thực hoặc tìm phần ảo của số phức

Ta biến đổi số phưc đã cho thành z = a + bi trong đó thì a và b là các số thực. Khi đó a là phần thực của z, còn b là phần ảo của z. Chú ý các bài toán về số phwusc mà hỏi về phần ảo người ta hay có phương án nhiễu nhiều.

Dạng 3: Dạng bài tập có số phức mũ cao

Cách tính số phức mũ cao là sử dụng dạng lượng giác hoặc dạng mũ của số phức. Với dạng lượng giác của số phức ta áp dụng công thức sau:

Dạng 4: Các dạng bài tập số phức liên quan đến phương trình bậc 2 với hệ số thực

Với phương trình bậc 2 hệ số thực trên tập số phức ta chia làm 2 nhóm: Nhóm bài tập liên quan đến việc tìm nghiệm và nhóm các bài tập liên quan đến định lý vi-et. Thông thường với phương trình không có tham số ta sử dụng máy tính bỏ túi để tính ra kết quả, còn nếu có tham số thì ta tính delta và thay vào công thức nghiệm hoặc sử dụng định lý vi-et

Xem thêm các bài viết liên quan hay, chi tiết

TOP 40 câu Trắc nghiệm Số phức (có đáp án 2024) - Toán 12

50 Bài tập Cộng, trừ và nhân số phức Toán 12 mới nhất

Câu 13:

Một hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?

A. 5

B. 3

C. 4

D. 6

Xem đáp án

Câu 14:

Họ nguyên hàm của hàm số f(x) = x-sin2x là

A. $\frac{x^{2}}{2} + \cos 2 x + C .$

B. $\frac{x^{2}}{2} + \frac{1}{2} \cos 2 x + C .$

C. $x^{2} + \frac{1}{2} \cos 2 x + C .$

D. $\frac{x^{2}}{2} - \frac{1}{2} \cos 2 x + C .$

Xem đáp án

Câu 15:

19/07/2024

Cho hình chóp SABCD, có đáy ABCD là hình vuông tâm O, cạnh bên vuông góc với mặt đáy. Gọi M là trung điểm của SA, N là hình chiếu vuông góc của A lên SO. Mệnh đề nào sau đây đúng?

A. $A C ⊥ (S B D) .$

B. $D N ⊥ (S A B) .$

C. $A N ⊥ (S O D) .$

D. $A M ⊥ (S B C) .$

Xem đáp án

Câu 16:

Gọi A, B lần lượt là các giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y = \frac{x^{2} + m^{2} + 2 m}{x - 2}$ trên đoạn [3;4]. Tìm tất cả các giá trị thực của tham số m để $A + B = \frac{19}{2} .$

A. $m = 1; m = - 3.$

B. $m = - 1; m = 3.$

C. $m = \pm 3.$

D. $m = - 4.$

Xem đáp án

Câu 17:

Giả sử hàm số f(x) liên tục trên đoạn [0;2] thỏa mãn $\int_{0}^{2} f (x) d x = 6.$ Tính tích phân $I = \int_{0}^{\frac{π}{2}} f (2 \sin x) \cos x d x .$

A. 3

B. -3

C. 6

D. -3

Xem đáp án

Câu 18:

19/07/2024

Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(-2;4) và B(8;4). Tìm tọa độ điểm C trên trục Ox, có hoành độ dương sao cho tam giác ABC vuông tại C.

A. C(3;0)

B. C(1;0)

D. (5;0)

D. (6;0)

Xem đáp án

Câu 19:

17/07/2024

Giá trị lớn nhất của hàm số $y = x^{2} + \frac{16}{x}$ trên đoạn $[\frac{3}{2}; 4]$ bằng:

A. 24

B. 20

C. 12

D. $\frac{155}{12}$

Xem đáp án

Câu 20:

18/07/2024

Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy hình trụ, AB=4a, AC=5a. Tính thể tích khối trụ:

A. $V = 8 π a^{3} .$

B. $V = 16 π a^{3} .$

C. $V = 12 π a^{3} .$

D. $V = 4 π a^{3} .$

Xem đáp án

Câu 21:

Cho hàm số $y = \log_{\frac{1}{2}} |x|$ . Mệnh đề nào dưới đây là mệnh đề sai?

A. Hàm số đã cho nghịch biến trên từng khoảng xác định.

B. Đồ thị hàm số đã cho không có tiệm cận ngang.

C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục tung.

D. Hàm số đã cho có tập xác định là $D = ℝ \ \{0\} .$

Xem đáp án

Câu 22:

Cho x là số thực dương, khai triển nhị thức ${(x^{2} + \frac{1}{x})}^{12}$ ta có hệ số của số hạng chứa x^m bằng 792: Giá trị của m là:

A. m=3 và m=9

B. m=0 và m=9

C. m=9

D. m=0

Xem đáp án

Câu 23:

14/07/2024

Tìm tập nghiệm S của phương trình 2^x⁺¹=4

A. $S = \{4\} .$

B. $S = \{1\} .$

C. $S = \{3\} .$

D. $S = \{2\} .$

Xem đáp án

Câu 24:

Cho tứ diện ABCD có $(A C D) ⊥ (B C D), A C = A D = B C = B D = A, C D = 2 A a .$ Giá trị của O để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là:

A. $\frac{a \sqrt{2}}{3} .$

B. $\frac{a \sqrt{3}}{3} .$

C. $\frac{a \sqrt{3}}{2} .$

D. $\frac{a \sqrt{5}}{3} .$

Xem đáp án

Câu 25:

Cho khối chóp SABCD có đáy là hình vuông cạnh $\frac{a}{\sqrt{2}}, Δ S A C$ vuông tại S và nằm trong mặt phẳng vuông góc với đáy, cạnh bên SA tạo với đáy góc $60^{o}$ . Tính thể tích V của khối chóp SABCD.

A. $V = \frac{a^{3} \sqrt{3}}{24} .$

B. $V = \frac{a^{3} \sqrt{3}}{12} .$

C. $V = \frac{a^{3} \sqrt{6}}{24} .$

D. $V = \frac{a^{3} \sqrt{2}}{24} .$

Xem đáp án

Câu 26:

14/07/2024

Cho tích phân $I = \int_{0}^{\frac{π}{4}} (x - 1) \sin 2 x d x$ . Đẳng thức nào sau đây là đúng?

A. $I = - (x - 1) \cos 2 x - \int_{0}^{\frac{π}{4}} \cos 2 x d x .$

B. $I = {- \frac{1}{2} (x - 1) \cos 2 x|}_{0}^{\frac{π}{4}} - \int_{0}^{\frac{π}{4}} \cos 2 x d x .$

C. $I = {- \frac{1}{2} (x - 1) \cos 2 x|}_{0}^{\frac{π}{4}} + \frac{1}{2} \int_{0}^{\frac{π}{4}} \cos 2 x d x .$

D. $I = {- (x - 1) \cos 2 x|}_{\begin{array}{l} 0 \end{array}}^{\frac{π}{4}} + \int_{0}^{\frac{π}{4}} \cos 2 x d x .$

Xem đáp án

Câu 27:

15/07/2024

Cho hàm số y = f(x) có đạo hàm cấp 2 trên khoảng K và $x_{o} \in K .$ Mệnh đề nào sau đây đúng?

A. Nếu f”(x₀)=0 thì x₀ là điểm cực trị của hàm số y = f(x)

B. Nếu x₀ là điểm cực trị của hàm số y = f(x) thì f”(x₀)≠0

C. Nếu x₀ là điểm cực trị của hàm số y = f(x) thì f’(x₀)=0

D. Nếu x₀ là điểm cực trị của hàm số y = f(x) thì f”(x₀)>0

Xem đáp án

Câu 28:

Tìm nguyên hàm của hàm số $f (x) = \frac{1}{x {(\ln x + 2)}^{2}}$

A. $\int f (x) d x = \frac{1}{\ln x + 2} + C .$

B. $\int f (x) d x = \frac{- 1}{\ln x + 2} + C .$

C. $\int f (x) d x = \frac{x}{\ln x + 2} + C .$

D. $\int f (x) d x = \ln x + 2 + C .$

Xem đáp án

Câu 29:

Tính tích tất cả các nghiệm của phương trình $2^{2 x^{2} + 5 x + 4} = 4$

A. 1

B. $\frac{5}{2}$

C. $- \frac{5}{2}$

D. $-$ 1

Xem đáp án

Câu 30:

Ký hiệu (H) là hình phẳng giới hạn bởi các đường $y = \sqrt{(x - 1) e^{x^{2} - 2 x}}; y = 0; x = 2$ . Tích thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành

A. $V = \frac{π (2 e - 1)}{2 e} .$

B. $V = \frac{π (2 e - 3)}{2 e} .$

C. $V = \frac{π (e - 1)}{2 e} .$

D. $V = \frac{π (e - 3)}{2 e} .$

Xem đáp án

Câu 31:

Trong không gian với hệ trục tọa độ Oxyz cho $\vec{a} = (1; - 2; 3)$ và $\vec{b} = (2; - 1; - 1)$ . Khẳng định nào sau đây đúng?

A. Vecto $\vec{a}$ không vuông góc với $\vec{b}$

B. Vecto $\vec{a}$ cùng phương với $\vec{b}$

C. $|\vec{a}| = \sqrt{14} .$

D. $[\vec{a}; \vec{b}] = (- 5; - 7; - 3)$

Xem đáp án

Câu 32:

Cho hình chóp S.ABCD có $S C = x (0 < x < a \sqrt{3}),$ các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi $x = \frac{a \sqrt{m}}{n} (m, n \in ℕ^{*})$ . Mệnh đề nào sau đây đúng?

A. $m + 2 n = 10.$

B. $2 m^{2} - 3 m < 15.$

C. $m^{2} - n = 30.$

D. $4 m - n^{2} = - 20.$

Xem đáp án

Câu 33:

Có bao nhiêu giá trị nguyên của tham số m để hàm số sau đạt cực tiểu tại $x = 0 : y = x^{8} + (m + 1) x^{5} - (m^{2} - 1) x^{4} + 1$

A. Vô số

B. 3

C. 2

D. 4

Xem đáp án

Câu 34:

19/07/2024

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình ${(x + 2 - \sqrt{x^{2} + 1})}^{2} + \frac{18 (x^{2} + 1) \sqrt{x^{2} + 1}}{x + 2 + \sqrt{x^{2} + 1}} = m (x^{2} + 1)$ có nghiệm thực?

A. 25

B. 2019

C. 2018

D. 2012

Xem đáp án

Câu 35:

Tìm tất cả các giá trị của tham số m để phương trình sau có đúng bốn nghiệm phân biệt ${(7 - 3 \sqrt{5})}^{x^{2}} + m {(7 + 3 \sqrt{5})}^{x^{2}} = 2 x^{2 - 1}$

A. $0 < m < \frac{1}{16} .$

B. $0 \leq m < \frac{1}{16} .$

C. $- \frac{1}{2} < m < 0.$

D. $- \frac{1}{2} < m \leq \frac{1}{16} .$

Xem đáp án

Câu 36:

Trong không gian với hệ tọa độ Oxyz, cho $A (- 3; 0; 0); B (0; 0; 3); C (0; - 3; 0)$ và mặt phẳng $(P) : x + y + z - 3 = 0.$ Tìm trên (P) điểm M sao cho $|\vec{M A} + \vec{M B} - \vec{M C}|$ nhỏ nhất

A. $M (3; 3; - 3) .$

B. $M (3; - 3; 3) .$

C. $M (- 3; 3; 3) .$

D. $M (- 3; - 3; 3) .$

Xem đáp án

Câu 37:

Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình $\log (2 x^{2} + 3) < \log (x^{2} + m x + 1)$ có tập nghiệm là R.

A. Vô số

B. 2

C. 5

D. 0

Xem đáp án

Câu 38:

Gọi M là giá trị lớn nhất của hàm số $f (x) = 6 \sqrt{x^{2} - 6 x + 12} + 6 x - x^{2} - 4$ .Tính tích các nghiệm của phương trình f(x)=M

A. -6

B. 3

C. -3

D. 6

Xem đáp án

Câu 39:

Gọi F(x) là một nguyên hàm của hàm số $f (x) = x^{3} - 2 x^{2} + 1$ thỏa mãn F(0)=5. Khi đó phương trình F(x)=5 có số nghiệm thực là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Câu 40:

Biết phương trình z²+mz+n=0 (với m, n là các tham số thực) có một nghiệm là z=1+i. Tính môđun của số phức z=m+ni

A. $2 \sqrt{2}$

B. 4

C. 16

D. 8

Xem đáp án

Câu 41:

Cho hàm số $f (x) = |\frac{x^{2} - m x + 2 m}{x - 2}|$ . Gọi S là tập hợp tất cả các giá trị của tham số m để $\max_{[- 1; 1]} f (x) \leq 5$ . Tổng tất cả các phần tử của S là:

A. -11

B. 9

C. -5

D. -1

Xem đáp án

Câu 42:

Một giải thi đấu bóng đá quốc gia có 12 đội bóng thi đấu vòng tròn hai lượt tính điểm (2 đội bất kì thi đấu với nhau đúng 2 trận). Sau mỗi trận đấu, đội thắng 3 điểm, đội thua 0 điểm, nếu hòa mỗi đội được 1 điểm. Sau giải đấu ban tổ chức thống kê được 60 trận hòa. Hỏi tổng số điểm của tất cả các đội sau giải đấu là

A. 336.

B. 630.

C. 360.

D. 306.

Xem đáp án

Đáp án A

Vì 12 đội bóng thi đấu vòng tròn hai lượt tính điểm (2 đội bất kì thi đấu với nhau đúng 2 trận) nên mỗi đội sẽ thi đấu với 11 đội còn lại, do đó tổng số trận đấu là 12.11 = 132 (trận).

Số trận hòa là 16 trận, số trận không hòa là 132 - 60 = 72.

60 trận hòa, mỗi đội được 1 điểm, vậy có 120 điểm.

72 trận không hòa, mỗi trận đội thắng được 3 điểm, vậy có 72.3 = 216 điểm.

Vậy tổng số điểm của tất cả các đội sau giải đấu là 120 + 126 = 336.

Câu 43:

Một hộp sữa hình trụ có thể tích V (không đổi) được làm từ một tấm tôn có diện tích đủ lớn. Nếu hộp sữa chỉ kín một đáy thì để tốn ít vật liệu nhất, hệ thức giữa bán kính đáy R và đường cao h bằng:

A. $h = \sqrt{3} R .$

B. $h = \sqrt{2} R .$

C. $h = 2 R .$

D. $h = R .$

Xem đáp án

Câu 44:

Bất phương trình $\log_{2}^{2} x - (2 m + 5) \log_{2} x + m^{2} + 5 m + 4 < 0$ đúng với mọi $x \in [2; 4)$ khi và chỉ khi

A. $m \in [0; 1) .$

B. $m \in [- 2; 0)$

C. $m \in (0; 1] .$

D. $m \in (- 2; 0] .$

Xem đáp án

Câu 45:

Cho tứ diện ABCD có $A D ⊥ (A B C), A B C$ có tam giác vuông tại B. Biết $B C = 2 a, A B = 2 a \sqrt{3}, A D = 6 a$ . Quay tam giác ABC và AB (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng AB ta được hai khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng:

A. $\frac{5 \sqrt{3} π a^{3}}{2} .$

B. $\frac{3 \sqrt{3} π a^{3}}{2} .$

C. $\frac{64 \sqrt{3} π a^{3}}{2} .$

D. $\frac{4 \sqrt{3} π a^{3}}{2} .$

Xem đáp án

Câu 46:

Cho hàm số y=f(x)xác định và liên tục trên R, có đạo hàm f’(x). Biết rằng đồ thị hàm số f’(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)=f(x)+x

A. Không có giá trị.

B. x=0

C. x=1

D. x=2

Xem đáp án

Câu 47:

Cho hàm số y = f(x) thỏa mãn ${[f' (x)]}^{2} + f (x) . f'' (x) = x^{3} - 2 x \forall x \in ℝ$ và f(0)=f’(0)=2. Tính giá trị của T=f²(2)

A. $\frac{268}{15} .$

B. $\frac{160}{15} .$

C. $\frac{268}{30} .$

D. $\frac{4}{15} .$

Xem đáp án

Câu 48:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D cạnh bên SA vuông góc với mặt đáy. Biết $A B = 2 A D = 2 D C = 2 a$ góc giữa hai mặt phẳng (SAB) và (SBC) là 60^o. Độ dài cạnh SA là:

A. $a \sqrt{2} .$

B. $2 a \sqrt{3} .$

C. $3 a \sqrt{2} .$

D. $a \sqrt{3} .$

Xem đáp án

Câu 49:

17/07/2024

Cho các hàm số $f_{o} (x), f_{1} (x), f_{2} (x), ...$ biết: $f_{o} (x) = \ln x + |\ln x - 2019| - |\ln x + 2019|, f_{n + 1} (x) = |f_{n} (x)| - 1, \forall n \in ℕ .$

Số nghiệm của phương trình $f_{2020} (x) = 0$ là

A. 6058.

B. 6057.

C. 6059.

D. 6063.

Xem đáp án

Câu 50: