Cho số phức z thỏa mãn $2z-i.\overline{z}=2+5i.$ Môđun của số phức z bằng

Đáp án đúng: B

*Lời giải:

*Phương pháp giải:

Áp dụng công thức tính modun số phức để tính

*Lý thuyến cần nắm và các dạng bài toán về

1. Số i.

Số i là số thỏa mãn: i2 = –1.

2. Định nghĩa số phức

Mỗi biểu thức dạng a + bi , trong đó $a;b\in R$; i2 = –1 được gọi là một số phức.

Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.

Tập hợp các số phức kí hiệu là C.

3. Số phức bằng nhau

– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :

a + bi = c + di a = c và b = d.

– Chú ý :

a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.

Như vậy, mỗi số thực cũng là một số phức. Ta có : $R\subset C$.

b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi

Đặc biệt : i = 0 + 1.i

Số i được gọi là đơn vị ảo.

4. Biểu diễn hình học số phức

Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.

 

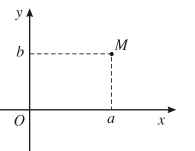
5. Mô đun của số phức.

Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.

Độ dài của vecto $\overrightarrow{OM}$ được gọi là môđun của số phức z và kí hiệu là |z|.

Vậy $\left|z\right|=\left|\overrightarrow{OM}\right|$hay $\left|a+bi\right|=\left|\overrightarrow{OM}\right|$.

Ta thấy: $\left|a+bi\right|=\sqrt{a^2+b^2}$

6. Số phức liên hợp

– Định nghĩa : Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hợp của z và kí hiệu là $\overline{z}=a-bi$.

– Nhận xét :

+ Trên mặt phẳng tọa độ các điểm biểu diễn z và $\overline{z}$ đối xứng nhau qua trục Ox.

+ Từ định nghĩa ta có: $\overline{\overline{z}}=z;\left|\overline{z}\right|=\left|z\right|$.

Các dạng bài tập số phức và cách giải

Dạng 1: Các dạng quỹ tích đơn giản căn bản

Đường thẳng: Quỹ tích các điểm M biểu diễn số phức z = x +yi là đường thẳng nếu như M (x;y) có tọa độ thỏa mãn phương trình đường thẳng: Ãx +By + C = 0

Đường tròn: QUỹ tích các điểm M biểu diễn số phức z = x + yi là đường tròn nếu như M(x; y) có tọa độ thỏa mãn phương trình đường tròn (C) : (x - a)2 + (b -y)2 = R2. Trong đó thì I (a; b) là tâm đường trong và R là bán kính đường tròn.

Đường elip: quỹ tích các điểm M biểu diễn số phức z = x +yi là đường elip nếu như M(x; y) có tọa độ thỏa mãn phương trình đường elip (E): $\frac{x^2}{a^2}+\frac{y^2}{b^2}$ = 1 trong đó thì a,b tương ứng với các bán trục lớn và bán trục nhỏ của elip

Dạng 2: Các dạng bài tập tìm phần thực hoặc tìm phần ảo của số phức

Ta biến đổi số phưc đã cho thành z = a + bi trong đó thì a và b là các số thực. Khi đó a là phần thực của z, còn b là phần ảo của z. Chú ý các bài toán về số phwusc mà hỏi về phần ảo người ta hay có phương án nhiễu nhiều.

Dạng 3: Dạng bài tập có số phức mũ cao

Cách tính số phức mũ cao là sử dụng dạng lượng giác hoặc dạng mũ của số phức. Với dạng lượng giác của số phức ta áp dụng công thức sau:

Dạng 4: Các dạng bài tập số phức liên quan đến phương trình bậc 2 với hệ số thực

Với phương trình bậc 2 hệ số thực trên tập số phức ta chia làm 2 nhóm: Nhóm bài tập liên quan đến việc tìm nghiệm và nhóm các bài tập liên quan đến định lý vi-et. Thông thường với phương trình không có tham số ta sử dụng máy tính bỏ túi để tính ra kết quả, còn nếu có tham số thì ta tính delta và thay vào công thức nghiệm hoặc sử dụng định lý vi-et

Xem thêm các bài viết liên quan hay, chi tiết

Lý thuyết Số phức (mới 2024 + Bài Tập) – Toán 12

TOP 40 câu Trắc nghiệm Số phức (có đáp án 2024) - Toán 12 

50 Bài tập Cộng, trừ và nhân số phức Toán 12 mới nhất