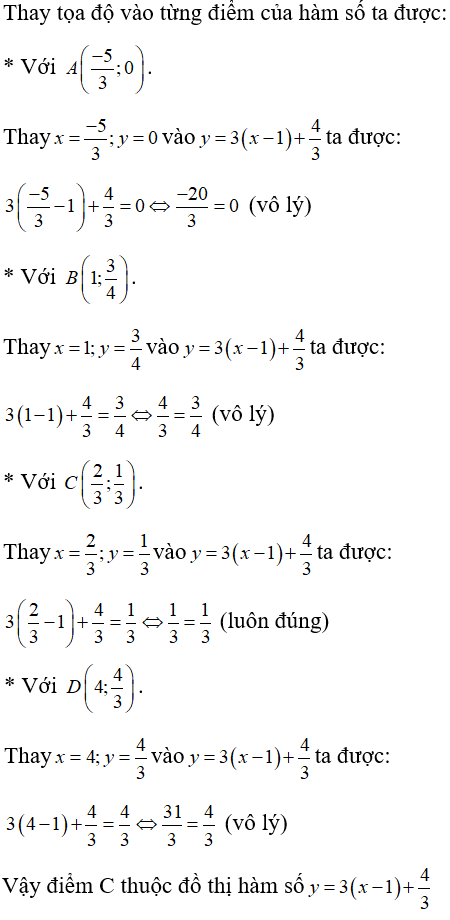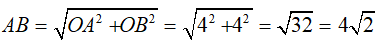21 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 9 Bài 3 (có đáp án): Đồ thị của hàm số y = ax + b

Câu 1:

23/07/2024

Chọn khẳng định đúng về đồ thị hàm số y = ax + b (a $\neq$ 0).

A. Là đường thẳng đi qua gốc tọa độ

B. Là đường thẳng song song với trục hoành

C. Là đường thẳng đi qua hai điểm $A (0; b), B (- \frac{b}{a}; 0)$ với $a, b \neq 0$

D. Là đường cong đi qua gốc tọa độ

Xem đáp án

Đáp án C

Đồ thị hàm số y = ax + b (a $\neq$ 0) là một đường thẳng

Trường hợp 1: Nếu b = 0 ta có hàm số y = ax .

Đồ thị y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a) .

Trường hợp 2: Nếu b $\neq$ 0 thì đồ thị y = ax + b là đường thẳng đi qua các điểm

.

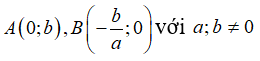Câu 2:

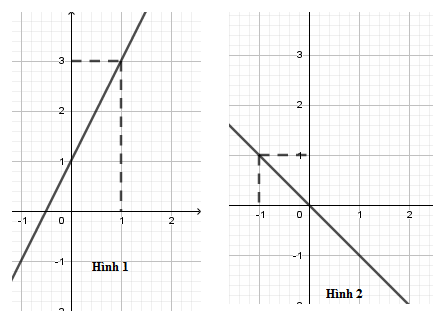
05/11/2024

Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số y = 2x + 1

A. Hình 4

B. Hình 2

C. Hình 3

D. Hình 1

Xem đáp án

Đáp án đúng là D

Lời giải

* Cho x = 0 ⇒ y = 1 ta được điểm A(0; 1) thuộc trục tung

Cho x = 1 ⇒ y = 3 ta được điểm B (1; 3)

* Đồ thị hàm số y = 2x + 1 đi qua hai điểm có tọa độ (0; 1) và (1; 3) nên hình 1 là đồ thị hàm số y = 2x + 1

*Phương pháp giải:

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Lập bảng giá trị (thường từ 3 đến 4 giá trị) tương ứng giữa x và y sao cho các điểm tương ứng nằm bên phải trục Oy.

Bước 3: Vẽ trục tọa độ Oxy và đánh dấu điểm O, các điểm đã lập trong bảng giá trị và các điểm đối xứng với chúng qua trục Oy.

Bước 4: Đồ thị hàm số y = a $x^{2}$ (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng. Vẽ đường cong parabol đi qua các điểm đã đánh dấu ta được đồ thị hàm số y = a $x^{2}$ (a ≠ 0) và kết luận.

*Lý thuyết:

- Đồ thị của hàm số: Đồ thị của hàm số y = a $x^{2}$ (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol)

+) Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.

+) Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.

Xem thêm

Các dạng bài tập Đồ thị hàm số y = a.x^2 (có đáp án 2024) và cách giải - Toán 9

TOP 40 câu Trắc nghiệm Đồ thị của hàm số y = ax + b (có đáp án 2024) – Toán 9

Câu 3:

14/07/2024

Đồ thị hàm số $y = 3 (x - 1) + \frac{4}{3}$ đi qua điểm nào dưới đây:

A. A $(\frac{- 5}{3}; 0)$

B. B $(1; \frac{3}{4})$

C. C $(\frac{2}{3}; \frac{1}{3})$

D. D $(4; \frac{4}{3})$

Xem đáp án

Đáp án C

Câu 4:

22/07/2024

Cho hai đường thẳng $d_{1}$ = 2x -2 và $d_{2}$ = 3 - 4x . Tung độ giao điểm của $d_{1}$ ; $d_{2}$ có tọa độ là:

A. $y = - \frac{1}{3}$

B. $y = \frac{2}{3}$

C. y = 1

D. y = -1

Xem đáp án

Đáp án A

Câu 5:

17/07/2024

Cho đường thẳng $d : y = 3 x - \frac{1}{2}$ . Giao điểm của với trục tung là:

A. A $(\frac{1}{6}; 0)$

B. B $(0; \frac{1}{2})$

C. C $(0; \frac{- 1}{6})$

D. D $(0; - \frac{1}{2})$

Xem đáp án

Đáp án D

Câu 6:

11/07/2024

Cho hai đường thẳng $d_{1}$ : y = 2x + 4 và $d_{2}$ : y = -x + 7. Tìm tọa độ giao điểm của hai đồ thị?

A. (1; 6)

B. (2 ; 8)

C. ( -1 ;2)

D. ( -2; 0)

Xem đáp án

Đáp án A

Phương trình hoành độ giao điểm của hai đồ thị:

2x + 4 = -x + 7

⇒ 2x + x = 7 -4

⇒ 3x = 3 ⇔ x = 1

Thay x = 1 vào phương trình đường thẳng y = 2x + 4 ta được: y = 2.1+ 4 = 6

Do đó, hai đồ thị đã cho cắt nhau tại A(1; 6)

Câu 7:

13/07/2024

Biết rằng với x = 2 thì hàm số y = 2x + b có giá trị là 10. Tìm b?

A. b = 3

B. b = 6

C. b = -3

D. b = 2

Xem đáp án

Đáp án C

Thay x = 2; y = 10 vào y = 2x + b ta được:

10 = 2.2 + b

Suy ra: b = 6

Câu 8:

17/07/2024

Biết rằng đồ thị hàm số y = ax - 10 đi qua điểm A( 1; -8). Tìm a?

A. 8

B.12

C. -8

D. 2

Xem đáp án

Đáp án D

Vì đồ thị hàm số đã cho đi qua A(1; -8) nên ta thay x = 1; y = -8 vào y = ax -10 ta được:

-8 = a.1 - 10 $\Leftrightarrow$ a = 2

Câu 9:

11/07/2024

Cho hàm số y = 3x + 12. Hỏi đồ thị hàm số cắt trục hoành tại điểm nào?

A. ( -4; 0)

B. (0;12)

C. (0; 4)

D. (12; 0)

Xem đáp án

Đáp án A

Cho y = 0 ⇒ 3x + 12 = 0 ⇔ x = -4

Do đó, đồ thị hàm số y = 3x + 12 cắt trục hoành tại điểm A( -4; 0)

Câu 10:

23/07/2024

Cho đồ thị hàm số y = -x + 4. Đồ thị hàm số cắt trục Ox, Oy lần lượt tại A; B. Tính khoảng cách AB?

A. 4

B. 4 $\sqrt{2}$

C. 8

D. 6 $\sqrt{2}$

Xem đáp án

Đáp án B

Cho x = 0 ⇒ y = 4 ta được điểm B(0;4) thuộc trục Oy.

Cho y = 0 ⇒ x = 4 ta được điểm A(4; 0) thuộc trục Ox.

Tam giác OAB vuông tại O có OA = 4 và OB = 4 nên:

Câu 11:

21/07/2024

Cho đường thẳng $d_{1} : y = - x + 2$ và đường thẳng $d_{2} : y = 5 - 4 x$ . Gọi A, B lần lượt là giao điểm của $d_{1}$ với $d_{2}$ và $d_{1}$ với trục hoành. Tổng hoành độ giao điểm của A và B là:

A. 2

B. 5

C. 3

D. 1

Xem đáp án

+) Phương trình hoành độ giao điểm của $d 1 v à d 2$ là:

$- x + 2 = 5 - 4 x \Leftrightarrow 3 x = 3 \Rightarrow x = 1 n ê n x_{A} = 1$

+) $B (x_{B}; 0)$ là giao điểm của đường thẳng d₁ và trục hoành. Khi đó ta có:

$= - x B + 2 \Rightarrow x B = 2$

Suy ra tổng hoành độ $x_{A} + x_{B} = 1 + 2 = 3$

Đáp án cần chọn là: C

Câu 12:

21/07/2024

Cho đường thẳng $d 1 : y = \frac{4 - x}{3} v à d 2 : y = 8 - 2 x$ . Gọi A, B lần lượt là giao điểm của $d 1 v ớ i d 2 v à d 1$ với trục tung. Tổng tung độ giao điểm của A và B là:

A. $\frac{4}{3}$

B. $\frac{2}{3}$

C. 9

D. 8

Xem đáp án

Phương trình hoành độ giao điểm của $d 1 v à d 2$ là:

$\frac{4 - x}{3} = 8 - 2 x \Leftrightarrow 24 - 6 x = 4 - x \Leftrightarrow 5 x = 20 \Rightarrow x = 4 \Rightarrow y = 0$ nên A (4; 0)

+) B (0; y_B) là giao điểm của đường thẳng d₁ và trục tung. Khi đó $y_{B} = \frac{4 - 0}{3}$

$y_{B} = \frac{4}{3}$

Suy ra tổng tung độ $y A + y B = 0 + \frac{4}{3} = \frac{4}{3}$

Đáp án cần chọn là: A

Câu 13:

22/07/2024

Cho đường thẳng $d : y = - 2 x - 4$ . Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Tính diện tích tam giác OAB.

A. 2

B. 4

C. 3

D. 8

Xem đáp án

A (x; 0) là giao điểm của d với trục hoành nên $0 = - 2 x \Leftrightarrow x = - 2 \Rightarrow A (- 2; 0)$

B (0; y) là giao điểm của d với trục tung nên $y = - 2.0 - 4 \Leftrightarrow y = - 4 \Rightarrow B (0; - 4)$

Suy ra $O A = | - 2 | = 2; O B = | - 4 | = 4$

Vì tam giác )AB vuông tại O nên $S_{O A B} = \frac{O A . O B}{2} = \frac{2.4}{2} = 4$ (đvdt)

Đáp án cần chọn là: B

Câu 14:

22/07/2024

Gọi $d_{1}$ là đồ thị hàm số $y = m x + 1 v à d_{2}$ là đồ thị hàm số $y = \frac{1}{2} x - 2$ . Xác định giá trị của m để M(2; −1) là giao điểm của ${d_{1} v à d}_{2}$ .

A. $m = 1$

B. $m = 2$

C. $m = - 1$

D. $m = - 2$

Xem đáp án

+) Nhận thấy $M \in d 2$

+) Ta thay tọa độ điểm M vào phương trình d₁ ta được phương trình

$- 1 = 2 . m + 1 \Leftrightarrow m = - 1$

Vậy $m = - 1$

Đáp án cần chọn là: C

Câu 15:

21/07/2024

Gọi d1 là đồ thị hàm số $y = - (2 m - 2) x + 4 m$ và $d 2$ là đồ thị hàm số $y = 4 x - 1$ . Xác định giá trị của m để M(1; 3) là giao điểm của d1 và d2.

A. $m = \frac{1}{2}$

B. $m = - \frac{1}{2}$

C. m = 2

D. m = −2

Xem đáp án

+) Nhận thấy $M \in d 2$

+) Ta thay tọa độ điểm M vào phương trình d1 ta được phương trình

$3 = - (2 m - 2) . 1 + 4 m \Leftrightarrow m = \frac{1}{2}$

Vậy $m = \frac{1}{2}$

Đáp án cần chọn là: A

Câu 16:

16/07/2024

Với giá trị nào của m thì ba đường thẳng $: y = (m + 2) x - 3; d 2 : y = 3 x + 1 v à d 3 : y = 2 x - 5$ giao nhau tại một điểm?

A. $m = \frac{1}{3}$

B. $m = - \frac{1}{3}$

C. $m = - 1$

D. $m = 1$

Xem đáp án

Xét phương trình hoành độ giao điểm của d2 và d3:

$3 x + 1 = 2 x - 5 \Leftrightarrow x = - 6 \Rightarrow y = - 17$ . Suy ra giao điểm của d2 và d3là M (−6; −17)

Để ba đường thẳng trên đồng quy thì M d2nên

$- 17 = (m + 2) . (- 6) - 3 \Leftrightarrow 6 (m + 2) = 14 \Leftrightarrow m = \frac{1}{3}$

Vậy $m = \frac{1}{3}$

Đáp án cần chọn là: A

Câu 17:

11/07/2024

Cho đường thẳng d: $y = - 3 x + 2 .$ Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Tính diện tích tam giác OAB.

A. $\frac{4}{3}$

B. $- \frac{2}{3}$

C. $\frac{3}{2}$

D. $\frac{2}{3}$

Xem đáp án

B (x; 0) là giao điểm của d với trục hoành nên $0 = - 3 x + 2 \Leftrightarrow x = \frac{2}{3} \Rightarrow B (\frac{2}{3}; 0)$

A (0; y) là giao điểm của d với trục tung nên $y = - 3.0 + 2 \Leftrightarrow y = 2 \Rightarrow A (0; 2)$

Suy ra $O A = | 2 | = 2; O B = |\frac{2}{3}| = \frac{2}{3}$

Vì tam giác OAB vuông tại O nên S_{OAB $= \frac{O A . O B}{2} = \frac{2. \frac{2}{3}}{2} = \frac{2}{3}$} (đvdt)

Đáp án cần chọn là: D

Câu 18:

11/07/2024

Với giá trị nào của m thì ba đường thẳng phân biệt $d 1 : y = (m + 2) x - 3 m - 3; d 2 : y = x + 2 v à d 3 : y = m x + 2$ giao nhau tại một điểm?

A. $m = \frac{1}{3}$

B. $m = - \frac{5}{3}$

C. $m = 1; m = - \frac{5}{3}$ ;

D. $m = - \frac{5}{6}$

Xem đáp án

Để 3 đường thẳng trên là ba đường thẳng phân biệt thì $\{\begin{cases} m + 2 \neq 1 \\ m \neq 1 \\ m \neq m + 2 \end{cases} \Leftrightarrow \{\begin{cases} m \neq 1 \\ m \neq - 1 \end{cases}$

Xét phương trình hoành độ giao điểm của $d 2 v à d 3 :$

$x + 2 = m x + 2 \Leftrightarrow x (m - 1) = 0 [\begin{array}{l} x = 0 \\ m = 1 (k t m) \end{array}$

Với $x = 0 \Rightarrow y = 2$ nên giao điểm của $d 2; d 3$ là M (0; 2)

Để ba đường thẳng trên giao nhau tại 1 điểm thì $M \in d 1$ nên:

$2 = (m + 2) . 0 - 3 m - 3 \Leftrightarrow 3 m = - 5 \Leftrightarrow m = - \frac{5}{3} (t m)$

Vậy $m = - \frac{5}{3}$

Đáp án cần chọn là: B

Câu 19:

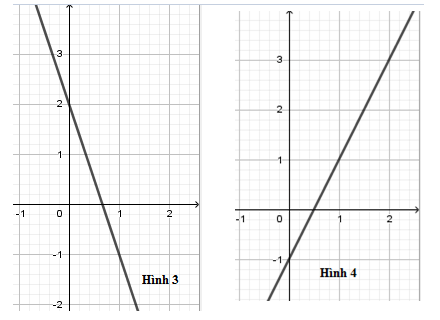
11/07/2024

Trong các hình vẽ sau, hình vẽ nào là đồ thị của hàm số $y = 3 x - 2$

A. Hình 4

B. Hình 2

C. Hình 3

D. Hình 1

Xem đáp án

Đồ thị hàm số $y = 3 x - 2$ là đường thẳng đi qua hai điểm có tọa độ (0; −2) và (1; 1) nên hình 2 là đồ thị hàm số $y = 3 x - 2 .$

Đáp án cần chọn là: B

Câu 20:

20/07/2024

Hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. $y = 2 x - 2$

B. $y = 3 x - 3$

C. $y = x - 1$

D. $y = x + 1$

Xem đáp án

Từ hình vẽ suy ra đồ thị hàm số đi qua hai diểm có tọa độ (1; 0) và (2; 3)

Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số $y = 3 x - 3$

+) Thay $x = 1; y = 0$ vào hàm số $y = 3 x - 3$ ta được $0 = 3 - 3 \Leftrightarrow 0 = 0$ (luôn đúng)

+) Thay $x = 2; y = 3$ vào hàm số $y = 3 x - 3$ ta được $3 = 3.2 - 3 \Leftrightarrow 3 =$ 3 (luôn đúng)

Vậy đồ thị hàm số $y = 3 x - 3$ là đường thẳng như hình vẽ.

Đáp án cần chọn là: B

Câu 21:

11/07/2024

Hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. $y = 2 x - 1$

B. $y = x - 1$

C. $y = x - 2$

D. $y = - 2 x - 1$

Xem đáp án

Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ (0; −1) và (2; 3)

Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số $y = 2 x - 1$

+) Thay $x = 0; y = 1$ vào hàm số $y = 2 x - 1$ ta được $1 = 2.0 - 1 \Leftrightarrow - 1 = - 1$

(luôn đúng)

+) Thay $x = 2; y = 3$ vào hàm số $y = 2 x - 1$ ta được $3 = 2.2 - 1 \Leftrightarrow 3 = 3$ (luôn đúng)

Vậy đồ thị hàm số $y = 2 x - 1$ là đường thẳng như hình vẽ.

Đáp án cần chọn là: A

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3