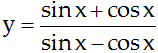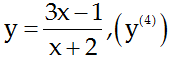100 câu trắc nghiệm Đạo hàm cơ bản (P1) (Đề số 4)
-
1258 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
14/11/2024Cho đường cong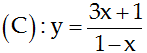 
. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng
(d): x - 4y – 21 = 0.
Xem đáp án
Đáp án đúng là C
Lời giải
Tập xác định D = R \ {1}. Ta có 
Có 
Vì tiếp tuyến song song với d nên ktt = kd = 1/4.
Gọi M(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(x0) = ktt 
⇔ (1- xo )2 = 16 ⇔ xo = 5 ∨ xo = -3
Với xo = 5 ⇒ yo = -4, phương trình tiếp tuyến tại điểm này là:
(loại, vì trùng với d).
Với xo = -3 ⇒ yo = -2, phương trình tiếp tuyến tại điểm này là:
Hay 4y = x - 5 x - 4y - 5 =0
*Phương pháp giải:
Dạng 1. Viết phương trình tiếp tuyến của đường tròn tại một điểm thuộc đường tròn
- Cho đường tròn (C): hoặc . Điểm thuộc đường tròn (C).
+ Nếu phương trình đường tròn có dạng thì phương trình tiếp tuyến là: .
+ Nếu phương trình đường tròn có dạng thì phương trình tiếp tuyến là:
*Lý thuyết:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính tại điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.
- Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
- Từ một điểm trên đường tròn ta có duy nhất một tiếp tuyến đi qua điểm đó. Từ một điểm ngoài đường tròn, ta có hai tiếp tuyến với đường tròn đi qua điểm đó.
Dạng 2. Viết phương trình tiếp tuyến của đường tròn tại một điểm ngoài đường tròn
- Cho đường tròn (C): hoặc . Điểm nằm ngoài đường tròn (C).
+ Viết phương trình của đường thẳng đi qua điểm N:
(1)
+ Có ta tính được m thay m vào phương trình (1) ta được phương trình tiếp tuyến. Ta luôn tìm được hai đường tiếp tuyến.
Dạng 3. Viết phương trình tiếp tuyến song song với phương cho sẵn có hệ số góc k
Phương trình đường thẳng (d) có dạng y = kx + m (m chưa biết)
kx - y + m = 0
Cho khoảng cách từ tâm I đến (d) = R ta tìm được m
Ta luôn tìm được 2 tiếp tuyến
Xem thêm
Phương trình tiếp tuyến của đường tròn (lý thuyết, công thức và cách giải các dạng bài tập)
Câu 2:
16/07/2024Cho đường cong 
Số tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng (Δ): 2x + 2y – 9 = 0.
Xem đáp án
Chọn B
Tập xác định D = R \ {1}. Ta có 
Vì tiếp tuyến vuông góc với Δ nên, 
Gọi N(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(xo) = ktt 
⇔ (1- xo )2 = 4 ⇔ xo = 3 ∨ xo = -1.
Với xo = 3 ⇒ y = -5, phương trình tiếp tuyến tại điểm này là:
⇔ y = 1(x – 3) – 5 ⇔ y = x – 8
Với xo = -1 ⇒ y = -1, phương trình tiếp tuyến tại điểm này là:
⇔ y = 1(x + 1) – 1 ⇔ y = x
Câu 3:
22/07/2024Cho hàm số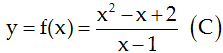 
.Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).
Xem đáp án
Chọn A.
Ta có: 
Ta có xo = 2 ⇒ f’(xo) = f’(2) = -1
Phương trình tiếp tuyến của (C) tại điểm M(2; 4) là
y = -1(x - 2) + 4 hay y = -x + 6.
Câu 4:
16/07/2024Cho hàm số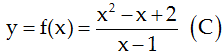
.
Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc k = 1.
Xem đáp án
Chọn D.
Ta có: 
Gọi xo là hoành độ tiếp điểm của tiếp tuyến với đồ thị, ta có f’(xo) = 1
(vô lý).
Kết luận không có tiếp tuyến nào có hệ số góc bằng 1.
Câu 5:
23/07/2024Cho hàm số (C):
. Tìm phương trình tiếp tuyến với (C). Tại điểm có hoành độ xo = 1/2.
Xem đáp án
Chọn A.
Ta có 
Với 
Vậy phương trình tiếp tuyến tại điểm 
là y = -2(x - 1/2) + 1/2
Hay y = -2x + 3/2.
Câu 7:
22/07/2024Tính đạo hàm của hàm số sau: y = cos2x
Xem đáp án
Chọn B.
Áp dụng công thức 
với u = cos x.
y’ = (cos2x)’ = 2.cosx. (cosx)’ = 2cosx.(-sinx) = -sin2x.
Câu 8:
16/07/2024Tính đạo hàm của hàm số sau: y = sin 3x.cos 5x
Xem đáp án
Chọn C.
= 4cos8x – cos2x.
Câu 12:
23/07/2024Giải phương trình y’ = 0 trong trường hợp sau: y = sin2x – 2cosx.
Xem đáp án
Chọn D.
Trước tiên, ta có: y’ = 2cos2x + 2sinx.
Khi đó, phương trình có dạng:
2cos2x + 2sinx = 0 
Câu 14:
23/07/2024Hàm số có đạo hàm là:
Xem đáp án
Chọn A.
Ta có
y’ = (sin2x)’.cosx + sin2x.(cosx)’ = 2cos2xsinx – sin3x
= sinx(2cos2x – sin2x) = sinx(3cos2x – 1).
Câu 15:
16/07/2024Hàm số y = x2.cosx có đạo hàm là:
Xem đáp án
Chọn A.
y' = (x2)’.cosx + x2(cosx)’ = 2x.cosx – x2.sinx.
Câu 16:
22/07/2024Cho hàm số y = cos3x.sin2x. Tính 
bằng:
Xem đáp án
Chọn B.
y' = (cos3x)’sin2x + cos3x(sin2x)’ = -3sin3x.sin2x + 2cos3x.cos2x.
. Chọn đáp án sai:
Giá trị 
bằng:
Câu 19:
22/07/2024Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
Xem đáp án
Chọn C.
y' = -2cosxsinx + cosx = cosx(1 – 2sinx)
Vì 
. Vậy có 3 nghiệm thuộc khoảng (0; π).
Câu 20:
20/07/2024Tính đạo hàm cấp ba của hàm số sau: y = xsin2x
Xem đáp án
Chọn D.
Có y’ = x’sin2x + x.(sin2x)’ = sin2x + 2xcos2x
⇒ y’’ = (sin2x)’ + (2x)’cos2x + 2x(cos2x)’
= 2 cos2x +2. cos2x + 2x. (- 2sin 2x )
= 4cos2x – 4xsin2x
⇒ y’’’ = 4(cos2x)’ – (4x)’sin2x – 4x(sin2x)’ = -8sin2x – 4sin2x – 8xcos2x
= -12sin2x – 8xcos2x.
Câu 21:
20/07/2024Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = cos2x,(y’’’)
Xem đáp án
Ta có 
⇒ y’’ = -2cos2x ⇒ y’’’ = 4sin2x.
Câu 22:
18/07/2024Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = x4 – sin2x, (y(4))
Xem đáp án
Chọn C.
y = x4 - sin2x
⇒ y’ = 4x3 – 2cos2x ⇒ y’’ = 12x2 + 4sin2x
⇒ y’’’ = 24x + 8cos2x ⇒ y(4) = 24 – 16sin2x
Câu 24:
22/07/2024Cho f(x) = (2x – 3)5. Khi đó f”(3) và f”’(3) lần lượt là:
Xem đáp án
Chọn A.
f’(x) = 5(2x – 3)4(2x – 3)’ = 10(2x – 3)4
f”(x) = 40(2x – 3)3(2x – 3)’ = 80(2x – 3)3
f”’(x) = 240(2x – 3)2(2x – 3)’ = 480(2x – 3)2
Vậy: f”(3) = 80(2.3 – 3)3 = 2160
f”’(3) = 480(2.3 – 3)2 = 4320
Câu 25:
16/07/2024Tính đạo hàm cấp hai của các hàm số sau: y = x2sinx
Xem đáp án
Chọn C.
y' = 2x.sinx + x2cosx
y” = 2sinx + 2xcosx + 2xcosx + x2(-sinx) = 2sinx + 4xcosx – x2sinx.