Trắc nghiệm Định nghĩa và ý nghĩa của đạo hàm (có đáp án)
Trắc nghiệm Toán 11 Bài 1: Định nghĩa và ý nghĩa của đạo hàm
-
721 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Vậy không tồn tại đạo hàm của hàm số tại .
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Ta có: f(1) = 5
Vậy hàm số không tồn tại đạo hàm tại .
Câu 3:
20/07/2024Khi tính đạo hàm của hàm số tại điểm , một học sinh đã tính theo các bước sau:
Bước 1:
Bước 2:
Bước 3:
Tính toán trên nếu sai thì sai ở bước nào?
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Bài giải trên hoàn toàn đúng.
Câu 4:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Đáp án:
Định nghĩa hay (nếu tồn tại giới hạn).
Câu 5:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
TXĐ:
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Đáp án:
Giả sử là số gia của đối số tại .
Ta có
Vậy
Câu 7:
17/07/2024Cho hàm số . Khi đó là kết quả nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
Câu 9:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
Giả sử là số gia của đối số tại .
Ta có
.
.
Vậy .
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Dễ thấy khi là hàm đa thức nên nó liên tục tại .
Ngoài ra
Do đó hàm số liên tục và có đạo hàm tại .
Xét các giới hạn
Do nên hàm số không liên tục tại .
Do đó, hàm số không có đạo hàm tại .
Câu 14:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Ta có:
Do đó không tồn tại giới hạn
Vậy hàm số không có đạo hàm tại .
Câu 15:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Ta có:
Do đó không tồn tại giới hạn
Vậy hàm số không có đạo hàm tại .
Câu 16:
19/07/2024Cho hàm số xác định: . Giá trị của bằng:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
Ta có:
Câu 17:
23/07/2024Cho hàm số . Xét hai mệnh đề sau:
(I) Hàm số có đạo hàm tại và
(II) Hàm số không có đạo hàm tại .
Mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
Ta có:
Hàm số không có đạo hàm tại x=0.
Câu 18:
23/07/2024Xét hai mệnh đề:
(I) có đạo hàm tại thì liên tục tại
(II) liên tục tại thì có đạo hàm tại
Mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
(I) hiển nhiên đúng.
(II) sai.
Ví dụ: Xét hàm số ta có
Hàm số liên tục tại trên nên cũng liên tục tại điểm x = 0
Tuy nhiên hàm số không có đạo hàm tại
Không tồn tại đạo hàm của hàm số tại .
Câu 19:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Đáp án:
Dựa vào nhận xét: Hàm số có đạo hàm tại thì liên tục tại . Điều ngược lại không đúng.
Ta thấy đáp án C đúng.
Câu 20:
19/07/2024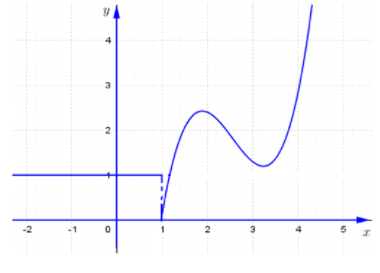
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
Dựa vào đồ thị hàm số ta thấy
Suy ra, không tồn tại , hàm số không liên tục tại .
Ngoài ra tại các điểm thì hàm số đều có đạo hàm.
Vậy hàm số không có đạo hàm tại .
Câu 21:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Đáp án:
Để hàm số có đạo hàm tại điểm thì trước hết hàm số phải liên tục tại , tức là
Khi đó hàm số có dạng:
Vậy .
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Ta có :
Nên
Vậy
Câu 23:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
Để hàm số có đạo hàm tại thì trước hết hàm số phải liên tục tại .
Ta có:
Để hàm số liên tục tại thì
Khi đó ta có:
Để tồn tại
.
Câu 24:
19/07/2024Xét hai hàm số: . Hàm số có đạo hàm tại là:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án:
Ta có: f(0) = 0
Hàm số có đạo hàm tại .
⇒ Hàm số không có đạo hàm tại .
Câu 25:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải
Vậy .
Câu 26:
21/07/2024Cho hàm số . Xét hai câu sau:
(1). Hàm số trên có đạo hàm tại x = 1
(2). Hàm số trên liên tục tại .
Trong hai câu trên:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải:
Ta có
+)
+)
+)
.
Vậy hàm số liên tục tại .
Mặt khác:
. Vậy hàm số không có đạo hàm tại .
Câu 27:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Ta có
nên hàm số liên tục tại
và
Vậy .
Câu 28:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Gọi là số gia của hàm số tại x= 1
Ta có:
Câu 30:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Đáp án:
Ta có:
Do đó không tồn tại , vậy không tồn tại đạo hàm của hàm số tại .
Có thể bạn quan tâm
- Trắc nghiệm Định nghĩa và ý nghĩa của đạo hàm (có đáp án) (720 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 1 (Có đáp án): Định nghĩa và ý nghĩa của đạo hàm (304 lượt thi)
- Trắc nghiệm Định nghĩa và ý nghĩa của đạo hàm có đáp án (phần 2) (456 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Đạo hàm nâng cao (P1) (2901 lượt thi)
- 100 câu trắc nghiệm Đạo hàm cơ bản (P1) (1521 lượt thi)
- Trắc nghiệm Quy tắc tính đạo hàm (có đáp án) (840 lượt thi)
- Trắc nghiệm Vi phân (có đáp án) (753 lượt thi)
- Trắc nghiệm Đạo hàm của hàm số lượng giác (có đáp án) (630 lượt thi)
- Trắc nghiệm Đạo hàm cấp hai (có đáp án) (518 lượt thi)
- Trắc nghiệm Ôn tập chương 5 (có đáp án) (508 lượt thi)
- Trắc nghiệm Đạo hàm cấp hai có đáp án có đáp án (479 lượt thi)
- Trắc nghiệm Các quy tắc tính đạo hàm có đáp án (phần 2) (465 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 2 (Có đáp án): Các quy tắc tính đạo hàm (366 lượt thi)
