26 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Bài 4: Vi phân

y = \sqrt{1 + \cos^{2} 2 x}

. Chọn kết quả đúng:

A.

d f (x) = \frac{- \sin 4 x}{2 \sqrt{1 + \cos^{2} 2 x}} d x

B.

d f (x) = \frac{- \sin 4 x}{\sqrt{1 + \cos^{2} 2 x}} d x

C.

d f (x) = \frac{\cos 2 x}{\sqrt{1 + \cos^{2} 2 x}} d x

D.

d f (x) = \frac{- \sin 2 x}{\sqrt{1 + \cos^{2} 2 x}} d x

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Ta có:

$\begin{array}{l} y' = \frac{{(1 + \cos^{2} 2 x)}^{'}}{2 \sqrt{1 + \cos^{2} 2 x}} \\ = \frac{2 c os2x. ( c os2x)'}{2 \sqrt{1 + \cos^{2} 2 x}} \\ = \frac{2 c os2x. (-2 sin2x)}{2 \sqrt{1 + \cos^{2} 2 x}} \\ = \frac{- \sin 4 x}{\sqrt{1 + \cos^{2} 2 x}} \\ d f (x) = \frac{- \sin 4 x}{\sqrt{1 + \cos^{2} 2 x}} d x \end{array}$

Câu 7:

. Khẳng định nào sau đây là sai:

f (x) = \{\begin{cases} x^{2} + x k h i x \geq 0 \\ x k h i x < 0 \end{cases}

A.

f^{'} (0^{+}) = 1

B.

f^{'} (0^{-}) = 1

C.

d f (0) = d x

D. Hàm số không có vi phân tại

x = 0

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có:

$\begin{array}{l} f^{'} (0^{+}) = \lim_{x \to 0^{+}} \frac{x^{2} + x}{x} \\ = \lim_{x \to 0^{+}} (x + 1) = 0 + 1 = 1; \end{array}$

$f^{'} (0^{-}) = \lim_{x \to 0^{-}} \frac{x}{x} = 1$ và $d f (0) = d x$ .

Câu 8:

17/07/2024

. Tính vi phân của hàm số tại

y = x^{3}

x_{0} = 1

với số gia

Δ x = 0, 01

.

A. $0, 01$

B.

3. {(0, 01)}^{2}

C. ${(0, 01)}^{3}$

D. $0, 03$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

$y' = 3 x^{2} \Rightarrow y' (1) = 3$

Vi phân của hàm số tại $x_{0} = 1$ với số gia $Δ x = 0, 01$ .

$d y (1) = y' (1) . Δ x = 3.0, 01 = 0, 03$

Câu 9:

Cho hàm số $y = \frac{x + 3}{1 - 2 x}$ . Vi phân của hàm số tại $x = - 3$ là:

A. $d y = \frac{1}{7} d x$

B. $d y = 7 d x$

C.

d y = - \frac{1}{7} d x

D. $d y = - 7 d x$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có:

$\begin{array}{l} y^{'} = \frac{(x + 3)' . (1 - 2 x) - (x + 3) . (1 - 2 x)'}{{(1 - 2 x)}^{2}} \\ = \frac{1 (1 - 2 x) - (x + 3) . (- 2)}{{(1 - 2 x)}^{2}} \\ = \frac{7}{{(1 - 2 x)}^{2}} \end{array}$

$\Rightarrow y^{'} (3) = \frac{1}{7} \Rightarrow d y = \frac{1}{7} d x$

Câu 10:

y = \cos^{2} 3 x

là:

A.

d y = 3 \sin^{2} 3 x d x

B. $d y = \sin 6 x d x$

C.

d y = - 3 \sin 6 x d x

D. $d y = 6 \sin 6 x d x$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

$\begin{array}{l} y^{'} = 2 \cos 3 x . (c os3x)' \\ = 2 c o s 3 x (- 3 \sin 3 x) \\ = - 3 \sin 6 x \\ \Rightarrow d y = - 3 \sin 6 x d x \end{array}$

Câu 11:

y = x^{3} - 5 x + 6

. Vi phân của hàm số là

A. $d y = (3 x^{2} - 5) d x$

B. $d y = - (3 x^{2} - 5) d x$

C. $d y = (3 x^{2} + 5) d x$

D. $d y = - (3 x^{2} - 5) d x$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có

$d y = {(x^{3} - 5 x + 6)}^{'} d x = (3 x^{2} - 5) d x$

Câu 12:

21/07/2024

y = \frac{1}{3 x^{3}}

. Vi phân của hàm số là:

A. $d y = \frac{1}{4} d x$

B. $d y = \frac{1}{x^{4}} d x$

C. $d y = - \frac{1}{x^{4}} d x$

D. $d y = x^{4} d x$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có

$\begin{array}{l} d y = {(\frac{1}{3 x^{3}})}^{'} d x \\ = \frac{1}{3} . \frac{- (x^{3})'}{{(x^{3})}^{2}} d x \\ = \frac{1}{3} . \frac{- 3 x^{2}}{{(x^{3})}^{2}} d x \\ = - \frac{1}{x^{4}} d x \end{array}$

Câu 13:

y = \sqrt{x \sqrt{x}}

là:

A. $d y = \frac{3}{4 \sqrt{\sqrt{x}}} d x$

B.

d y = \frac{3}{2 \sqrt{\sqrt{x}}} d x

C.

d y = \frac{5}{4 \sqrt{x}} d x

D.

d y = \frac{1}{2 \sqrt{x}} d x

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$\begin{array}{l} y' = \frac{1}{2 \sqrt{x \sqrt{x}}} . (x \sqrt{x})' \\ = \frac{1}{2 \sqrt{x \sqrt{x}}} (\sqrt{x} + x . \frac{1}{2 \sqrt{x}}) \end{array}$

$\begin{array}{l} = \frac{1}{2 \sqrt{x \sqrt{x}}} . \frac{3}{2} \sqrt{x} = \frac{3}{4} . \frac{\sqrt{x}}{\sqrt{x \sqrt{x}}} \\ = \frac{3}{4} . \sqrt{\frac{x}{x \sqrt{x}}} \\ = \frac{3}{4} . \sqrt{\frac{1}{\sqrt{x}}} = \frac{3}{4} . \frac{1}{\sqrt{\sqrt{x}}} \end{array}$

Vi phân của hàm số đã cho là:

$d y = \frac{3}{4 \sqrt{\sqrt{x}}} d x$

Câu 14:

Vi phân của hàm số là:

y = \frac{\tan \sqrt{x}}{\sqrt{x}}

A. $d y = \frac{2 \sqrt{x}}{4 x \sqrt{x} \cos^{2} \sqrt{x}} d x$

B. $d y = \frac{\sin (2 \sqrt{x})}{4 x \sqrt{x} \cos^{2} \sqrt{x}} d x$

C. $d y = \frac{2 \sqrt{x} - \sin (2 \sqrt{x})}{4 x \sqrt{x} \cos^{2} \sqrt{x}} d x$

D. $d y = - \frac{2 \sqrt{x} - \sin (2 \sqrt{x})}{4 x \sqrt{x} \cos^{2} \sqrt{x}} d x$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có

$\begin{array}{l} dy = {(\frac{\tan \sqrt{x}}{\sqrt{x}})}^{'} dx \\ = \frac{\frac{1}{2 \sqrt{x}} . \frac{1}{\cos^{2} \sqrt{x}} . \sqrt{x} - \tan \sqrt{x} . \frac{1}{2 \sqrt{x}}}{x} dx \end{array}$

$\begin{array}{l} = (\frac{1}{2} . \frac{1}{\cos^{2} \sqrt{x}} - \frac{\sin \sqrt{x}}{\cos \sqrt{x}} . \frac{1}{2 \sqrt{x}}) \frac{1}{x} dx \\ = \frac{\sqrt{x} - \sin \sqrt{x} \cos \sqrt{x}}{2 x \sqrt{x} . \cos^{2} \sqrt{x}} . d x \end{array}$

Câu 15:

19/07/2024

. Mệnh đề nào sau đây đúng:

y = x + \sqrt{x^{2} + 1}

A.

\sqrt{1 + x^{2}} . d y - y d x = 0

B.

\sqrt{1 + x^{2}} . d x - d y = 0

C.

x d x + \sqrt{1 + x^{2}} . d y = 0

D.

\sqrt{1 + x^{2}} . d y + x y = 0

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có:

$d y = y^{'} d x \Rightarrow y^{'} = \frac{d y}{d x}$ mà

$\begin{array}{l} y' = 1 + \frac{(x^{2} + 1)'}{2 \sqrt{x^{2} + 1}} \\ = 1 + \frac{x}{\sqrt{x^{2} + 1}} \\ = \frac{\sqrt{x^{2} + 1} + x}{\sqrt{x^{2} + 1}} \\ = \frac{y}{\sqrt{x^{2} + 1}} \end{array}$

$\begin{array}{l} \Rightarrow \frac{d y}{d x} = \frac{y}{\sqrt{x^{2} + 1}} \\ \Leftrightarrow \sqrt{x^{2} + 1} d y - y d x = 0 \end{array}$

Câu 16:

Dùng vi phân tính gần đúng

\sqrt[3]{26, 7}

có giá trị là:

A. 2,999

B. 2,98

C. 2,97

D. 2,89

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Xét $f (x) = \sqrt[3]{x}$ thì $f^{'} (x) = \frac{1}{3. \sqrt[3]{x^{2}}}$ .

Cho $x_{0} = 27, Δ x = - 0, 3$ .

Theo công thức gần đúng

$f (x_{0} + Δ x) \approx f^{'} (x_{0}) . Δ x + f (x_{0})$

$\Rightarrow \sqrt[3]{27, 3} \approx \sqrt[3]{27} + \frac{1}{27} (- 0, 3) \approx 2, 999.$

Câu 17:

Dùng vi phân tính gần đúng

\sin 29 °

có giá trị là:

A. 0,4849

B. 0,5464

C. 0,4989

D. 0,4949

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Xét $f (x) = \sin x$ với $29 ° = \frac{π}{6} - \frac{π}{180} (r a d)$ .

Có $f^{'} (x) = \cos x$ .

Chọn $x_{0} = \frac{π}{6}$ , $Δ x = - \frac{π}{180}$

$\Rightarrow \sin (\frac{π}{6} - \frac{π}{180}) \approx \sin \frac{π}{6} + \cos (\frac{π}{6}) . (- \frac{π}{180}) \approx 0, 4849$

Câu 18:

16/07/2024

Với hàm số

x^{2} y + y^{3} = 2

thì đạo hàm

y^{'}

tại điểm

(1; 1)

bằng:

A.

- \frac{3}{2}

B. -1

C.

- \frac{1}{2}

D. 0

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

$\begin{array}{l} x^{2} y + y^{3} = 2 \\ \Rightarrow d (x^{2} y) + d (y^{3}) = 0 \\ \Leftrightarrow 2 x y d x + x^{2} d y + 3 y^{2} d y = 0 \end{array}$

tại điểm $(1; 1)$ ta có:

$\begin{array}{l} 2 d x + d y + 3 d y = 0 \\ \Rightarrow 4 d y = - 2 d x \\ \Rightarrow \frac{d y}{d x} = - \frac{1}{2} = y^{'} (1) \end{array}$

Câu 19:

Cho hàm số $y = \sin (\sin x)$ . Vi phân của hàm số là:

A.

d y = \cos (\sin x) . \sin x d x

B. $d y = \sin . (\cos x) . d x$

C. $d y = \cos (\sin x), \cos x d x$

D. $d y = \cos (\sin x) d x$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

$\begin{array}{l} y^{'} = c os( sin x). (sinx)' \\ = cosx . c o s (\sin x) \end{array}$

$\Rightarrow d y = \cos x . c o s (\sin x) d x$

Câu 20:

y = \frac{x \sin x + \cos x}{x \cos x - \sin x}

bằng:

A.

d y = \frac{d x}{{(x \cos x - \sin x)}^{2}}

B.

d y = \frac{x^{2} d x}{{(x \cos x - \sin x)}^{2}}

C.

d y = \frac{\cos x d x}{{(x \cos x - \sin x)}^{2}}

D.

d y = \frac{x^{2} \sin x d x}{{(x \cos x - \sin x)}^{2}}

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Ta có :

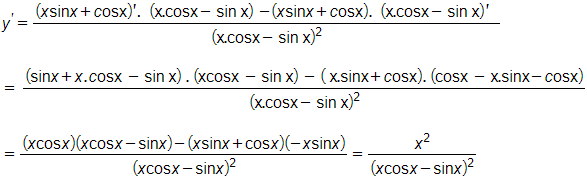
Vi phân của hàm số đã cho là $d y = \frac{x^{2} d x}{{(x \cos x - \sin x)}^{2}}$

Câu 21:

nhận kết quả nào sau đây?

Xét hàm số

f^{'} (x) = x^{2} - 1

. Nếu đặt

y = f (x^{2})

thì

\frac{d y}{d x}

A. $2 x (x^{4} - 1)$

B.

2 x (x^{2} - 1)

C. $x^{4} - 1$

D. $x^{2} - 1$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Đặt $u = x^{2} \Rightarrow y = f (u)$

Từ $f^{'} (x) = x^{2} - 1 \Rightarrow f^{'} (u) = u^{2} - 1$

$\begin{array}{l} \Rightarrow \frac{d y}{d x} = \frac{d y}{d u} . \frac{d u}{d x} \\ = f^{'} (u) . \frac{d u}{d x} \\ = (u^{2} - 1) 2 x \\ = 2 x (x^{4} - 1) \end{array}$

Câu 22:

21/07/2024

Xét hàm số $y = x^{2}$ . Gọi $Δ x, d y$ theo thứ tự là số gia và vi phân của hàm số y tại $x_{0} = 1$ và $d x = 0, 01$ . Hiệu của $Δ y - d y$ bằng:

A. 0,001

B. 0,002

C. 0,0001

D. 0,00001

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có: $y' = 2 x \Rightarrow y' (1) = 2$

Chọn $Δ x = d x = 0, 01; x_{0} = 1 \Rightarrow y_{0} = 1$

$\begin{array}{l} d y = 2.0, 01 = 0, 02 \\ \Rightarrow Δ y - d y = 0, 0001 \end{array}$

Câu 23:

Xét $\cos y = \sin^{2} x (0 < y < \frac{π}{2}, 0 < x < \frac{π}{2})$ . Đạo hàm của y tại $x = \frac{π}{4}$ là:

A. $\frac{π}{6}$

B. $\frac{π}{3}$

C.

\frac{- 2}{\sqrt{3}}

D.

\frac{- \sqrt{3}}{2}

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

$\cos y = \sin^{2} x \Rightarrow - \sin y d y = \sin 2 x d x$

$\Rightarrow \frac{d y}{d x} = \frac{\sin 2 x}{- \sin y} = \frac{\sin 2 x}{- \sqrt{1 - \cos^{2} y}}$ (vì $\sin y > 0$ )

$\Rightarrow \frac{d y}{d x} = y^{'} = \frac{- \sin \frac{π}{2}}{\sqrt{1 - \sin^{4} \frac{π}{4}}} = - \frac{2}{\sqrt{3}}$

Câu 24:

y = \frac{- 2 x^{2} - 2 x + 1}{{(x^{2} + x + 1)}^{2}}

là:

A. $d y = \frac{2 (2 x + 1) (x^{2} + x - 2)}{{(x^{2} + x + 1)}^{3}} d x$

B.

d y = \frac{(2 x + 1) (x^{2} - x + 1)}{{(x^{2} + x + 1)}^{3}} d x

C.

d y = \frac{(3 x - 1) (x^{2} - 2 x + 5)}{{(x^{2} + x + 1)}^{3}} d x

D. $d y = \frac{(x + 1) (x^{2} + x - 2)}{{(x^{2} + x + 1)}^{3}} d x$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$\begin{array}{l} y^{'} = \frac{(- 4 x - 2) {(x^{2} + x + 1)}^{2} - (- 2 x^{2} - 2 x) 2 (x^{2} + x + 1) (2 x + 1)}{{(x^{2} + x + 1)}^{4}} \\ = \frac{2 (x^{2} + x + 1) . (2 x + 1) . [- (x^{2} + x + 1) - (- 2 x^{2} - 2 x)]}{{(x^{2} + x + 1)}^{4}} \end{array}$

$= \frac{2 (2 x + 1) (x^{2} + x - 2)}{{(x^{2} + x + 1)}^{3}}$

Vi phân của hàm số đã cho là $d y = \frac{2 (2 x + 1) (x^{2} + x - 2)}{{(x^{2} + x + 1)}^{3}} d x$

Câu 25:

Tính vi phân của hàm số

y = \sin \sqrt{x^{2} + ​ \sin (c osx)}

A. $d y = \frac{c os \sqrt{x^{2} + \sin (c osx)}}{2 \sqrt{x^{2} + \sin (c osx)}} . [2 x + c os(sinx)] dx$

B. $d y = \frac{c os \sqrt{x^{2} + \sin (c osx)}}{\sqrt{x^{2} + \sin (c osx)}} . [2 x - \sin x (sinx) . c os x] dx$

C. $d y = \frac{c os \sqrt{x^{2} + \sin (c osx)}}{\sqrt{x^{2} + \sin (c osx)}} . [2 x - \sin x (sinx) . c os x] dx$

D. Đáp án khác

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

$\begin{array}{l} y' = c os \sqrt{x^{2} + \sin (c osx)} . (\sqrt{x^{2} + \sin (c osx)})' \\ = c os \sqrt{x^{2} + \sin (c osx)} . \frac{1}{2 \sqrt{x^{2} + \sin (c osx)}} . (x^{2} + \sin (c osx))' \\ = \frac{c os \sqrt{x^{2} + \sin (c osx)}}{2 \sqrt{x^{2} + \sin (c osx)}} . [2 x + c os(sinx) . (c osx)'] \\ = \frac{c os \sqrt{x^{2} + \sin (c osx)}}{2 \sqrt{x^{2} + \sin (c osx)}} . [2 x - c os(sinx) . \sin x] \end{array}$

Do đó, vi phân của hàm số là

$d y = \frac{c os \sqrt{x^{2} + \sin (c osx)}}{2 \sqrt{x^{2} + \sin (c osx)}} . [2 x - c os(sinx) . \sin x] dx$

Câu 26: