• Logo VietJack.me
×
Trang chủ Lớp 11 Toán Trắc nghiệm Ôn tập chương 5 (có đáp án)

Trắc nghiệm Ôn tập chương 5 (có đáp án)

Trắc nghiệm Toán 11 Ôn tập chương 5

  • 438 lượt thi

  • 28 câu hỏi

  • 45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

21/07/2024
Đạo hàm của hàm số fx=2x+1 tại x0=1 là
Xem đáp án

Chọn A.

Ta có: f'(x)=2⇒f'(2)=2.

Câu 2:

22/07/2024
Vi phân của hàm số y=2x5−2x+5 là biểu thức nào dưới đây?
Xem đáp án

Chọn D.

Ta có:  

dy=2x5−2x+5'dx

=10x4+2x2dx.

Câu 3:

19/07/2024
Cho hàm số y=fx có đồ thị C và điểm Mx0;y0∈C. Khi đó, tiếp tuyến của C tại điểm M có hệ số góc là
Xem đáp án
Chọn A.

Câu 4:

17/07/2024
Đạo hàm của hàm số y=x là
Xem đáp án

Chọn C.

Ta có:  

y=x⇒y'=12x.

Câu 5:

23/07/2024
Đạo hàm của hàm số y=cosx là
Xem đáp án
Chọn D.

Câu 6:

17/07/2024
Hàm số y=sinx+x có đạo hàm là
Xem đáp án

Chọn B.

Theo bảng công thức đạo hàm của những hàm số thường gặp.

Câu 7:

21/07/2024
Đâu là phương trình tiếp tuyến của đồ thị hàm số y=fx tại điểm Mx0;y0?
Xem đáp án
Chọn D.

Câu 8:

20/07/2024
Tính đạo hàm của hàm số  y=x2+1
Xem đáp án

Chọn C.

Ta có  

y'=x2+1'=2x.

Câu 9:

19/07/2024
Cho hàm số y=sinx. Tính y''0
Xem đáp án

Chọn A.

Ta có  y'=cosx, y''=−sinx.

⇒y''0=−sin0=0.

Câu 10:

23/07/2024
Cho hàm số y=fx có đạo hàm trên tập số thực. Tìm hệ thức đúng.
Xem đáp án
Chọn A. 

Câu 11:

23/07/2024
Cho hàm số y= f (x)  có đạo hàm đến cấp 2 trên tập số thực. Tìm hệ thức đúng.
Xem đáp án
Chọn B.

Câu 12:

21/07/2024
Lập phương trình tiếp tuyến của đồ thị hàm số y=x2+3x+1 tại điểm có hoành độ bằng 1.
Xem đáp án

Chọn A.

Ta có  y'=2x+3.

Với x0=1⇒y'1=5y0=5.

Vậy phương trình tiếp tuyến cần tìm là  

Δ:y=5x−1+5⇔y=5x.

Câu 13:

22/07/2024
Cho chuyển động thẳng xác định bởi phương trình: St=t3+3t2−9t+27, trong đó t tính bằng giây  và S được tính bằng mét. Gia tốc của chuyển động tại thời điểm vận tốc triệt tiêu là
Xem đáp án

Chọn D.

Vận tốc của chuyển động lúc t là  

vt=S'=t3+3t2−9t+27'=3t2+6t–9.

Gia tốc của chất điểm lúc t là  

at=v'=3t2+6t−9'=6t+6.

Vận tốc triệt tiêu khi

vt=0⇔3t2+6t−9=0⇒t=1.

Do đó  a1=6.1+6=12  m/s2

Câu 14:

22/07/2024
Cho hàm số y=12x4−mx−3x. Có bao nhiêu giá trị nguyên dương của tham số m để y'≥0 với mọi x thuộc khoảng 0;+∞?
Xem đáp án

Chọn A.

y=12x4−mx−3x⇒y'=2x3−m+3x2

y'≥0 với mọi x thuộc khoảng  0;+∞

⇔m≤2x3+3x2∀∈0;+∞

Dấu "="  xảy ra khi  

x3=1x2⇔x=1.

Vậy 1⇔m≤5.

m là số nguyên dương ⇒m∈1;2;3;4;5.

Câu 15:

22/07/2024
Cho hàm số fx=ax3+bx3+cx2. Biết f2=954, f'1=16, f'−1=8. Khi đó tính tổng  a+b+c
Xem đáp án

Chọn B.

Ta có:  f'x=3ax2−3bx4+2cx.

• f2=954⇔8a+b8+4c=954  1 

•  f'1=16⇔3a−3b+2c=16 2

•  f'−1=8⇔3a−3b−2c=8  3 

Từ 1, 2 và 3 suy ra: a=2b=−2c=2 .

Vậy a+b+c=2.

Câu 16:

23/07/2024

Hệ số góc k của tiếp tuyến với đồ thị hàm số y=2x+1x+1 tại giao điểm của đồ thị hàm số với trục tung là?
Xem đáp án

Chọn C.

Hàm số y=2x+1x+1 có tập xác định: 

D=ℝ\−1;y'=1x+12,∀x≠−1

Đồ thị hàm số cắt trục tung tại điểm A0;1.

Tiếp tuyến của đồ thị hàm số tại điểm A0;1 có hệ số góc

k=y'0=10+12=1.

Câu 17:

23/07/2024
Một chuyển động có phương trình st=t2−2t+3 (trong đó s tính bằng mét, t tính bằng giây). Vận tốc tức thời của chuyển động tại thời điểm t=2s là
Xem đáp án

Chọn A.

Ta có phương trình vận tốc là vt=s't=2t2−2 suy ra

v2=6  m/s.

Câu 18:

23/07/2024
Cho hàm số fx=x2+3. Tính giá trị của biểu thức S=f1+4f'1.
Xem đáp án

Chọn B.

Ta có  

fx=x2+3⇒f'x=xx2+3.

Vậy

 S=f1+4f'1=12+3+4.112+3=4.

Câu 19:

11/12/2024
Cho hàm số fx=−x3+3mx2−12x+3 với m là tham số thực. Số giá trị nguyên của m để f'x≤0 với ∀x∈ℝ  là
Xem đáp án

Đáp án đúng là B.

Lời giải

Ta có  

fx=−x3+3mx2−12x+3⇒f'x=−3x2+6mx−12.

f'x≤0 với ∀x∈ℝ

⇔−3x2+6mx−12≤0 với ∀x∈ℝ

⇔Δ'≤0⇔9m2−36≤0⇔−2≤m≤2.

Do m là số nguyên nên m∈−2;−1;0;1;2.

Vậy có 5 giá trị nguyên của m.

*Phương pháp giải:

Bước 1: Tính y'=f'x;m=ax2+bx+c.

Bước 2: Hàm số đơn điệu trên x1;x2⇔y'=0 có 2 nghiệm phân biệt

⇔Δ>0a≠0  *

Bước3: Kết luận

*Lý thuyết

- Định nghĩa:

Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:

Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) nhỏ hơn f(x2), tức là

x1 < x2 ⇒ f(x1) < f(x2).

Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) lớn hơn f(x2), tức là

x1 < x2 ⇒f(x1) > f(x2).

- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.

- Nhận xét: Từ định nghĩa trên ta thấy:

a) f(x) đồng biến trên K⇔f(x2)−f(x1)x2−x1  >​0  ;  ∀x1; x2  ∈K;  (x1 ≠x2)

f(x) nghịch biến trên K⇔f(x2)−f(x1)x2−x1  < ​0  ;  ∀x1; x2  ∈K;  (x1 ≠x2)

b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.

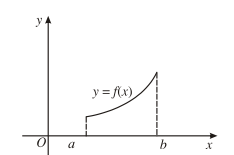
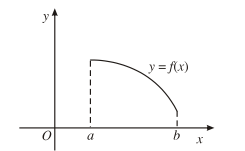
Lý thuyết Sự đồng biến, nghịch biến của hàm số chi tiết – Toán lớp 12 (ảnh 1)

Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.

Lý thuyết Sự đồng biến, nghịch biến của hàm số chi tiết – Toán lớp 12 (ảnh 1)

2. Tính đơn điệu và dấu của đạo hàm

- Định lí:

Cho hàm số y = f(x) có đạo hàm trên K.

a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

- Chú ý:

Nếu f’(x) = 0 với ∀x ∈   ​K   thì f(x) không đổi trên K.

- Chú ý:

Ta có định lí mở rộng sau đây:

Giả sử hàm số y = f(x) có đạo hàm trên K. Nếu f'(x)  ≥0   f'(x) ≤0  ;  ∀x∈K 

Và f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.

Xem thêm

Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2 + Bài Tập) – Toán 12 

 

Câu 20:

21/07/2024
Vi phân của hàm số y=cos2x+cotx là
Xem đáp án

Chọn D.

Ta có  

dy=dcos2x+cotx=−2sin2x−1sin2xdx.

Câu 21:

16/07/2024
Cho hàm số fx=2x+112. Tính f''0.
Xem đáp án

Chọn B.

Ta có  

f'x=122x+1112x+1'=242x+111

Suy ra  

f''x=24.112x+110(2x+1)'=5282x+110⇒f''0=528.

Câu 22:

16/07/2024
Hệ số góc của tiếp tuyến của đồ thị hàm số y=x−1x+1 tại điểm có hoành độ x0=0 là
Xem đáp án

Chọn D.

Ta có

y'=2x+12 suy ra hệ số góc của tiếp tuyến tại điểm có hoành độ x0=0 là

k=y'0=2.

Câu 23:

16/07/2024
Tìm số gia Δy của hàm số y=x2 biết x0=3 và Δx=−1.
Xem đáp án

Chọn C.

Ta có

 Δy=yx0+Δx−yx0=y2−y3=22−32=−5.

Câu 24:

16/07/2024
Cho hàm số y=x2+3x+1. Nếu y'>0 thì x thuộc tập hợp nào sau đây:
Xem đáp án

Chọn A.

Ta có  

y'=x2+3'x+1−x2+3x+1'x+12=x2+2x−3x+12

Suy ra

y'>0⇔x2+2x−3x+12>0⇔x2+2x−3>0x≠−1⇔x>1x<−3x≠−1⇔x>1x<−3.

Câu 25:

22/07/2024
Cho hàm số y=cos2x2−x+7. Khi đó y' bằng
Xem đáp án

Chọn C.

Ta có  

y'=cos2x2−x+7'=−2x2−x+7'sin2x2−x+7

=−2x2−x+7'22x2−x+7sin2x2−x+7=1−4xsin2x2−x+722x2−x+7

Câu 26:

20/07/2024
Gọi C là đồ thị của hàm số y=x−13. Tiếp tuyến của C song song với đường thẳng Δ:12x−y−2018=0 có phương trình là
Xem đáp án

Chọn D.

Ta có  y'=3x−12.

Δ:12x−y−2018=0⇔y=12x−2018.

Gọi Mm;m−13 là tiếp điểm. Ta có

y'm=3m−12=12⇔m=3m=−1.

 m=3

⇒d:y=12(x−3)+8=12x−28 (thỏa)

m=−1

⇒d:y=12(x+1)−8=12x+4 (thỏa).

Câu 27:

16/07/2024
Tiếp tuyến của đồ thị hàm số y=x3+2x−4 tại điểm M0;−4 có phương trình là
Xem đáp án

Chọn D.

Ta có y'=3x2+2, hoành độ tiếp điểm x0=0 nên:

Hệ số góc của tiếp tuyến: y'0=2.

Tung độ tiếp điểm là y0=−4.

Phương trình tiếp tuyến cần tìm là

y=2(x−0)−4

Câu 28:

22/07/2024
Đạo hàm của hàm số y=12sin2x+cosx tại x0=π2 bằng
Xem đáp án

Chọn D.

Ta có  

y'=122x'cos2x−sinx=cos2x−sinx

nên y'π2=cosπ−sinπ2=−2.

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương