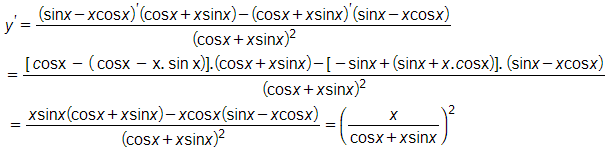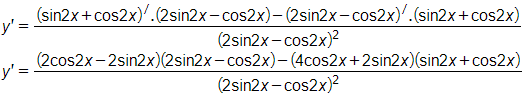Trắc nghiệm Đạo hàm của hàm số lượng giác (có đáp án)
Trắc nghiệm Toán 11 Bài 3: Đạo hàm của hàm số lượng giác
-
632 lượt thi
-
31 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Ta có:
Do đó
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Bước đầu tiên áp dụng
Tính : Áp dụng , với ta được:
Tương tự:
Kết luận:
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải:
Suy ra
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Áp dụng , với
Tính áp dụng với u = sin2x
Câu 18:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Áp dụng , với u= cos2x
Câu 19:
17/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : B
Lời giải:
*Phương pháp giải:
Tính đạo hàm y'
Quy đồng mẫu
sử dụng công thức lượng giác
*Lý thuyết:
với
với
Câu 22:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
Sử dụng công thức đạo hàm hợp: và đạo hàm của hàm số lượng giác.
Ta có:
Câu 25:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Ta có:
Câu 26:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải:
Ta có:
Suy ra:
Câu 29:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Áp dụng với
Tính bước đầu sử dụng sau đó sử dụng
Vậy
Câu 30:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải:
Áp dụng với
Tính
Vậy
Có thể bạn quan tâm
- Trắc nghiệm Đạo hàm của hàm số lượng giác (có đáp án) (631 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 3 (Có đáp án): Đạo hàm của các hàm số lượng giác (297 lượt thi)
- Trắc nghiệm Đạo hàm của các hàm số lượng giác có đáp án (phần 2) (289 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Đạo hàm nâng cao (P1) (2908 lượt thi)
- 100 câu trắc nghiệm Đạo hàm cơ bản (P1) (1522 lượt thi)
- Trắc nghiệm Quy tắc tính đạo hàm (có đáp án) (842 lượt thi)
- Trắc nghiệm Vi phân (có đáp án) (754 lượt thi)
- Trắc nghiệm Định nghĩa và ý nghĩa của đạo hàm (có đáp án) (721 lượt thi)
- Trắc nghiệm Đạo hàm cấp hai (có đáp án) (520 lượt thi)
- Trắc nghiệm Ôn tập chương 5 (có đáp án) (509 lượt thi)
- Trắc nghiệm Đạo hàm cấp hai có đáp án có đáp án (480 lượt thi)
- Trắc nghiệm Các quy tắc tính đạo hàm có đáp án (phần 2) (466 lượt thi)
- Trắc nghiệm Định nghĩa và ý nghĩa của đạo hàm có đáp án (phần 2) (456 lượt thi)