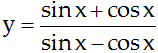Câu hỏi:
14/11/2024 215Cho đường cong 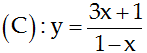 . Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng
. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng
(d): x - 4y – 21 = 0.
A. y = -x -1/4
B. 2y + 4x – 1 = 0
C. x - 4y – 5 = 0
D. Đáp án khác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là C
Lời giải
Tập xác định D = R \ {1}. Ta có
Có
Vì tiếp tuyến song song với d nên ktt = kd = 1/4.
Gọi M(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(x0) = ktt
⇔ (1- xo )2 = 16 ⇔ xo = 5 ∨ xo = -3
Với xo = 5 ⇒ yo = -4, phương trình tiếp tuyến tại điểm này là:
(loại, vì trùng với d).
Với xo = -3 ⇒ yo = -2, phương trình tiếp tuyến tại điểm này là:
Hay 4y = x - 5 ⇔x - 4y - 5 =0
*Phương pháp giải:
Dạng 1. Viết phương trình tiếp tuyến của đường tròn tại một điểm thuộc đường tròn
- Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm M(x0;y0) thuộc đường tròn (C).
+ Nếu phương trình đường tròn có dạng x2+y2−2ax−2by+c=0 thì phương trình tiếp tuyến là: xx0+yy0−a(x+x0)−b(y+y0)+c=0.
+ Nếu phương trình đường tròn có dạng (x−a)2+(y−b)2=R2 thì phương trình tiếp tuyến là: (x−a)(x0−a)+(y−b)(y0−b)=R2
*Lý thuyết:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính tại điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.
- Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
- Từ một điểm trên đường tròn ta có duy nhất một tiếp tuyến đi qua điểm đó. Từ một điểm ngoài đường tròn, ta có hai tiếp tuyến với đường tròn đi qua điểm đó.
Dạng 2. Viết phương trình tiếp tuyến của đường tròn tại một điểm ngoài đường tròn
- Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm N(x0;y0) nằm ngoài đường tròn (C).
+ Viết phương trình của đường thẳng đi qua điểm N:
y−y0=m(x−x0)⇔mx−y−mx0+y0=0 (1)
+ Có d(I,d)=R ta tính được m thay m vào phương trình (1) ta được phương trình tiếp tuyến. Ta luôn tìm được hai đường tiếp tuyến.
Dạng 3. Viết phương trình tiếp tuyến song song với phương cho sẵn có hệ số góc k
Phương trình đường thẳng (d) có dạng y = kx + m (m chưa biết)
kx - y + m = 0
Cho khoảng cách từ tâm I đến (d) = R ta tìm được m
Ta luôn tìm được 2 tiếp tuyến
Xem thêm
Phương trình tiếp tuyến của đường tròn (lý thuyết, công thức và cách giải các dạng bài tập)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Giải phương trình y’ = 0 trong trường hợp sau: y = sin2x – 2cosx.
Câu 9:
Cho hàm số 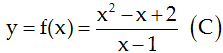 .Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).
.Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).
Câu 12:
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
Câu 14:
Cho hàm số (C):![]() . Tìm phương trình tiếp tuyến với (C). Tại điểm có hoành độ xo = 1/2.
. Tìm phương trình tiếp tuyến với (C). Tại điểm có hoành độ xo = 1/2.

 bằng:
bằng: