Nội dung bài viết

    Xem thêm

    Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC)

    Với giải bài tập 2 trang 50 sgk Toán lớp 12 Hình học được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

    1 1,748 02/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Bài 3: Ôn tập chương 2

    Bài 2 trang 50 SGK Toán lớp 12 Hình học: Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Biết AB = AD = a. Tính diện tích xung quanh của hình nón và thể tích của khối nón được tạo thành khi quay đường gấp khúc BDA quanh cạnh AB.

    *Lời giải

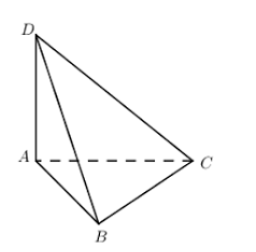
    Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) (ảnh 1)

    Ta có: AD  ⊥  (ABC) nên AD  ⊥AB.

    Suy ra: tam giác ABD vuông tại A và ABD^  <​  900.

    Khi quay xung quanh cạnh AB; tam giác ABD tạo ra hình nón tròn xoay có đỉnh B; trục là đường thẳng AB, đáy là hình tròn tâm A – bán kính r = AD .

    Vậy hình nón có: Chiều cao h = BA = a; bán kính r = AD = a; đường sinh l=  BD​ =  AD2+​​AB2  =a2.

    Diện tích xung quanh của hình nón là:

    Sxq =  πrl  =π.a.a2  = π.a22

    Thể tích của khối nón là:

    V  =  13πr2h=   13πa2.a= 13πa3.

    *Phương pháp giải

    - ápd dụng công thức tính Sxq và V hình nón để tính:

    Sxq  =  πrl (r là bán kính đường tròn đáy, l là độ dài đường sinh).

    V=13B.h

    *Lý thuyến cần nắm về mặt nón, mặt trụ, mặt cầu:

    Hình nón tròn xoay và khối nón tròn xoay.

    a) Cho tam giác OIM vuông tại I. Khi quay tam giác đó xung quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.

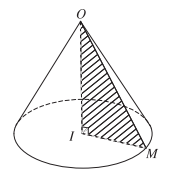
    Lý thuyết Khái niệm về mặt tròn xoay chi tiết – Toán lớp 12 (ảnh 1)

    Hình tròn tâm I sinh bởi các điểm thuộc cạnh IM khi quay quanh trục OI được gọi là mặt đáy của hình nón, điểm O được gọi là đỉnh của hình nón.

    Độ dài đoạn OI gọi là chiều cao của hình nón, đó cũng chính là khoảng cách từ O đến mặt phẳng đáy. Độ dài đoạn OM gọi là độ dài đường sinh của hình nón.

    Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh OM khi quay quanh OI được gọi là mặt xung quanh của hình nón đó.

    b) Khối nón tròn xoay là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó. Người ra gọi tắt khối nón tròn xoay là khối nón.

    Những điểm không thuộc khối nón được gọi là những điểm ngoài của khối nón. Những điểm thuộc khối nón nhưng không thuộc hình nón ứng với khối nón ấy được gọi là những điểm trong của khối nón.

    Ta gọi đỉnh, mặt đáy, đường sinh của một hình nón theo thứ tự là đỉnh, mặt đáy, đường sinh của khối nón tương ứng.

    Diện tích xung quanh của hình nón tròn xoay.

    a) Một hình chóp được gọi là nội tiếp một hình nón nếu đáy của hình chóp là đa giác nội tiếp đường tròn đáy của hình nón và đỉnh của hình chóp là đỉnh của hình nón. Khi đó, ta còn nói hình nón ngoại tiếp hình chóp.

    - Định nghĩa: Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.

    b) Công thức tính diện tích xung quanh của hình nón.

    - Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh.

    Sxq  =  πrl (r là bán kính đường tròn đáy, l là độ dài đường sinh).

    - Người ta gọi tổng của diện tích xung quanh và diện tích đáy là diện tích toàn phần của hình nón.

    - Chú ý: Diện tích xung quanh, diện tích toàn phần của hình nón tròn xoay cũng là diện tích xung quanh , diện tích toàn phần của khối nón được giới hạn bởi hình nón đó.

    Thể tích khối nón tròn xoay.

    a) Định nghĩa.

    Thể tích của khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh đáy tăng lên vô hạn.

    b) Công thức tính thể tích khối nón tròn xoay.

    Gọi V là thể tích của khối nón tròn xoay có diện tích đáy B và chiều cao h, ta có công thức: V=13B.h

    Như vậy, nếu bán kính đáy bằng r thì B=πr2, khi đó:

    Xem thêm các bài viết liên quan hay, chi tiết:

    Lý thuyết Mặt nón, mặt trụ, mặt cầu hay, chi tiết

    Giải Toán 12 Chương 2 vở bài tập : Mặt nón, mặt trụ, mặt cầu

    TOP 40 câu Trắc nghiệm Ôn tập Chương 2: Mặt nón. Mặt trụ. Mặt cầu (có đáp án 2024) - Toán 12

    Xem thêm lời giải bài tập Toán lớp 12 hay, chi tiết khác:

    Bài 1 trang 50 Toán lớp 12 Hình học: Cho ba điểm A, B, C cùng thuộc một mặt cầu...

    Bài 3 trang 50 Toán lớp 12 Hình học: Chứng minh rằng hình chóp có tất cả các cạnh bên bằng nhau nội tiếp được trong một mặt cầu...

    Bài 4 trang 50 Toán lớp 12 Hình học: Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh bên SA, SB, SC...

    Bài 5 trang 50 Toán lớp 12 Hình học: Cho tứ diện đều ABCD cạnh a...

    Bài 6 trang 50 Toán lớp 12 Hình học: Cho hình vuông ABCD cạnh a...

    Bài 7 trang 50 Toán lớp 12 Hình học: Cho hình trụ có bán kính r, trục OO' = 2r ...

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,748 02/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: