Câu hỏi:
21/07/2024 304
Trên nóc tòa nhà có một cột ăng – ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
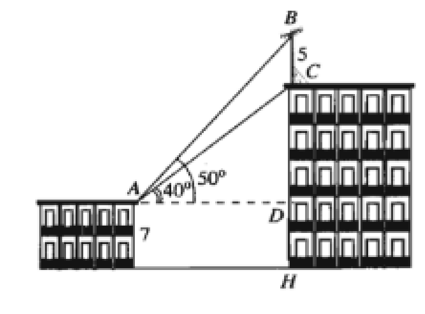
Trên nóc tòa nhà có một cột ăng – ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?

A. 12m;
A. 12m;
B. 19m;
C. 29m;
D. 24m.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
Gọi điểm H là chân tòa nhà. Điểm D là điểm tương ứng trên tòa nhà ngang bằng với vị trí quan sát A. Như vậy = 90°.
Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Như vậy = 40° và = 50°.
Xét tam giác ABD có: = 180 – – = 180° – 90° – 50° = 40° = .
Xét tam giác ABC có:
= 50° – 40° = 10°.
Áp dụng định lí sin cho tam giác ABC:
⇒ ⇒ AC ≈ 18,5m
Áp dụng định lí sin cho tam giác ADC:
⇒ CD ≈ 11,9m
Chiều cao tòa nhà tương ứng với đoạn CH.
CH = CD + DH = 11,9 + 7 = 18,9 ≈ 19m.
Vậy đáp án đúng là B.
Hướng dẫn giải
Đáp án đúng là: B
Gọi điểm H là chân tòa nhà. Điểm D là điểm tương ứng trên tòa nhà ngang bằng với vị trí quan sát A. Như vậy = 90°.
Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Như vậy = 40° và = 50°.
Xét tam giác ABD có: = 180 – – = 180° – 90° – 50° = 40° = .
Xét tam giác ABC có:
= 50° – 40° = 10°.
Áp dụng định lí sin cho tam giác ABC:
⇒ ⇒ AC ≈ 18,5m
Áp dụng định lí sin cho tam giác ADC:
⇒ CD ≈ 11,9m
Chiều cao tòa nhà tương ứng với đoạn CH.
CH = CD + DH = 11,9 + 7 = 18,9 ≈ 19m.
Vậy đáp án đúng là B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Đề bài: Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu tới B chạy với tốc độ 20 hải lí một giờ. Tàu tới C chạy với tốc độ 15 hải lí một giờ. Hỏi sau hai giờ hai tàu cách nhau bao nhiêu hải lí? ( Chọn kết quả gần nhất ).
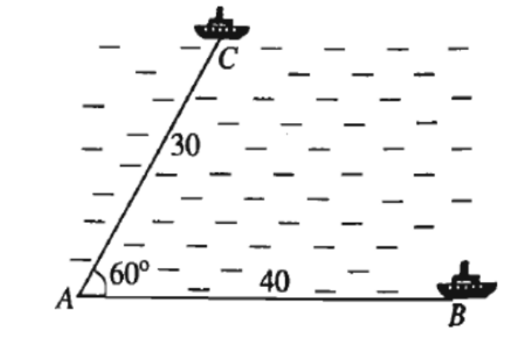
Đề bài: Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu tới B chạy với tốc độ 20 hải lí một giờ. Tàu tới C chạy với tốc độ 15 hải lí một giờ. Hỏi sau hai giờ hai tàu cách nhau bao nhiêu hải lí? ( Chọn kết quả gần nhất ).

Câu 2:
Cho tam giác ABC có AB = 4, BC = 6, AC = 2 . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.
Câu 3:
Tam giác ABC có AB = , BC = , CA = . AD là tia phân giác trong của . Tính .
Tam giác ABC có AB = , BC = , CA = . AD là tia phân giác trong của . Tính .
Câu 4:
Tam giác ABC có BC = a, AC = b, AB = c. Các cạnh a, b, c liên hệ với nhau bằng đẳng thức b.( b2 – a2 ) = c.( a2 – c2 ). Tính .
Tam giác ABC có BC = a, AC = b, AB = c. Các cạnh a, b, c liên hệ với nhau bằng đẳng thức b.( b2 – a2 ) = c.( a2 – c2 ). Tính .


