Thi Online Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác (phần 2) có đáp án
Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác (Vận dụng ) có đáp án
-
485 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
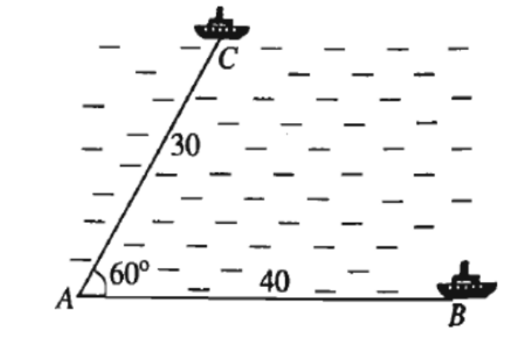
27/10/2024Đề bài: Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu tới B chạy với tốc độ 20 hải lí một giờ. Tàu tới C chạy với tốc độ 15 hải lí một giờ. Hỏi sau hai giờ hai tàu cách nhau bao nhiêu hải lí? ( Chọn kết quả gần nhất ).
Xem đáp án
Đáp án đúng là: B
*Lời giải
Sau 2h, tàu tới C đi được đoạn đường b = 15.2 = 30 ( hải lí )
Sau 2h, tàu tới B đi được đoạn đường c = 15.2 = 40 ( hải lí )
Dựa vào hình vẽ, sau 2h, tàu B và tàu C tạo với điểm xuất phát một tam giác ABC có
= 60°, b = 30, c = 40 và a = BC.
Áp dụng định lí côsin ta có:
a2 = b2 + c2 – 2bccosA
a2 = 302 + 402 – 2.30.40.cos60°
a2 = 1300
a ≈ 36 ( hải lí )
*Phương pháp giải
Dựa vào hình minh họa ta xác định được quãng đường của hai tàu sau hai giờ, dựa vào dữ kiện đề bài cho biết hướng tạo bởi 2 tàu là 60° nên chúng ta áp dụng định lí cosin để tính được sau hai giờ 2 tàu cách nhau bao xa.
* Lý thuyết cần nắm thêm về hệ thức lượng trong tam giác:
Định lí Côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
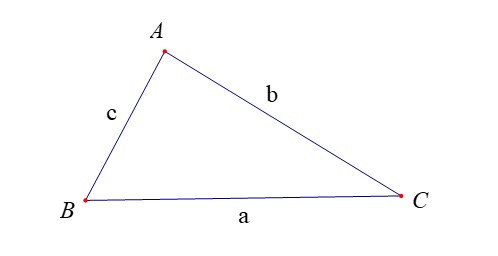
Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
Định lí sin
Trong tam giác ABC: .
Giải tam giác và ứng dụng thực tế
- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.
Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:
+ Biết hai cạnh và góc xen giữa.
+ Biết ba cạnh.
+ Biết một cạnh và hai góc kề.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hệ thức lượng trong tam giác – Toán 10 Kết nối tri thức
Giải bài tập Toán 10 Bài 3: Giải tam giác và ứng dụng thực tế
Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án
Câu 2:
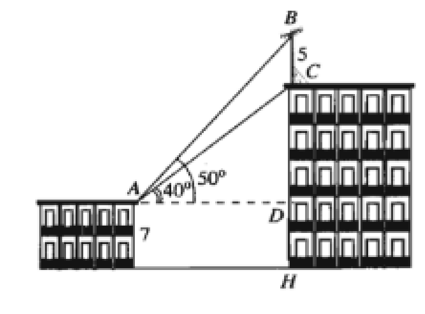
21/07/2024Trên nóc tòa nhà có một cột ăng – ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Gọi điểm H là chân tòa nhà. Điểm D là điểm tương ứng trên tòa nhà ngang bằng với vị trí quan sát A. Như vậy = 90°.
Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Như vậy = 40° và = 50°.
Xét tam giác ABD có: = 180 – – = 180° – 90° – 50° = 40° = .
Xét tam giác ABC có:
= 50° – 40° = 10°.
Áp dụng định lí sin cho tam giác ABC:
⇒ ⇒ AC ≈ 18,5m
Áp dụng định lí sin cho tam giác ADC:
⇒ CD ≈ 11,9m
Chiều cao tòa nhà tương ứng với đoạn CH.
CH = CD + DH = 11,9 + 7 = 18,9 ≈ 19m.
Vậy đáp án đúng là B.
Câu 3:
22/07/2024Tam giác ABC có BC = a, AC = b, AB = c. Các cạnh a, b, c liên hệ với nhau bằng đẳng thức b.( b2 – a2 ) = c.( a2 – c2 ). Tính .
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
b.( b2 – a2 ) = c.( a2 – c2 )
⟺ b3 – a2b – a2c + c3 = 0
⟺ b3 + c3 – ( a2b + a2c ) = 0
⟺ ( b + c )( b2 – bc + c2 ) – a2( b + c ) = 0
⟺ ( b + c ) ( b2 + c2 – a2 – bc ) = 0
b và c là cạnh tam giác nên b + c > 0
⇒ b2 + c2 – a2 – bc = 0 hay a2 = b2 + c2 – bc
Theo định lí côsin
a2 = b2 + c2 – 2bccosA
mà a2 = b2 + c2 – bc ⇒ cosA = ⇒ = 60°.
Vậy đáp án đúng là D.
Câu 4:
14/07/2024Tam giác ABC có AB = , BC = , CA = . AD là tia phân giác trong của . Tính .
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
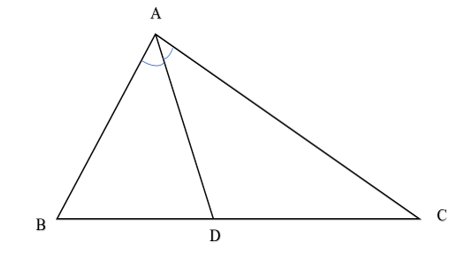
Đặt AB = c, BC = a, AC = b
Theo định lí côsin ta có: a2 = b2 + c2 – 2bccosA
⇒ cosA =
⇒ cosA =
⇒ cosA =
⇒ = 120° hay = 120°.
Tương tự: cosB =
⇒ cosB =
⇒ cosB =
⇒ = 45° hay = 45°
AD là tia phân giác trong của = 60°.
Xét tam giác ABD: = 180°
⇒ = 180° –= 180° – 60° – 45° = 75°
Vậy đáp án C đúng.
Câu 5:
14/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Đặt AB = c = 4, AC = b = 2 , BC = a = 6.
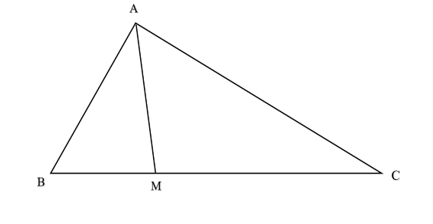
Áp dụng định lí côsin cho tam giác ABC:
b2 = a2 + c2 – 2accosB
⇒ cosB =
⇒ cosB =
BC = 6 và MC = 2MB ⇒ MC = 4 và MB = 2.
Áp dụng định lí côsin cho tam giác ABM:
AM2 = AB2 + BM2 – 2.AM.BM.cos
AM2 = 42 + 22 – 2.2.4.
AM =
Vậy đáp án đúng là C.