Câu hỏi:
14/07/2024 1,445
Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh rằng →BN=→NM.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Gọi tọa độ điểm N(a; b).
Ta có: →AN=(a−2;b−3), →NC=(3−a;(−1)−b).
Vì N là trung điểm của đoạn thẳng AC nên →AN=→NC
⇔{a−2=3−ab−3=(−1)−b⇔{2a=52b=2⇔{a=52b=1.
Vậy tọa độ của điểm N là N(52;1).
Ta có: →BN=(52−(−1);1−1)=(72;0); →NM=(6−52;1−1)=(72;0)
Vậy →BN=→NM.
Hướng dẫn giải:
Gọi tọa độ điểm N(a; b).
Ta có: →AN=(a−2;b−3), →NC=(3−a;(−1)−b).
Vì N là trung điểm của đoạn thẳng AC nên →AN=→NC
⇔{a−2=3−ab−3=(−1)−b⇔{2a=52b=2⇔{a=52b=1.
Vậy tọa độ của điểm N là N(52;1).
Ta có: →BN=(52−(−1);1−1)=(72;0); →NM=(6−52;1−1)=(72;0)
Vậy →BN=→NM.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho vectơ →u (Hình 7). Hãy xác định điểm A sao cho →OA=→u.
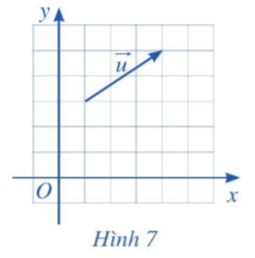
Trong mặt phẳng tọa độ Oxy, cho vectơ →u (Hình 7). Hãy xác định điểm A sao cho →OA=→u.

Câu 5:
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2; 3), B(– 1; 1), C(3; – 1).
Tìm toạ độ điểm M sao cho →AM=→BC.
Câu 6:
Tìm điểm M sao cho →OM=→AB. Từ đó, tìm hoành độ a và tung độ b của vectơ →AB.
Câu 7:
Trong mặt phẳng toạ độ Oxy, cho điểm M(– 1; 3).
Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
Trong mặt phẳng toạ độ Oxy, cho điểm M(– 1; 3).
Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
Câu 9:
B. Bài tập
Tìm tọa độ của các vectơ trong Hình 16 và biểu diễn mỗi vectơ đó qua hai vectơ →i và →j.
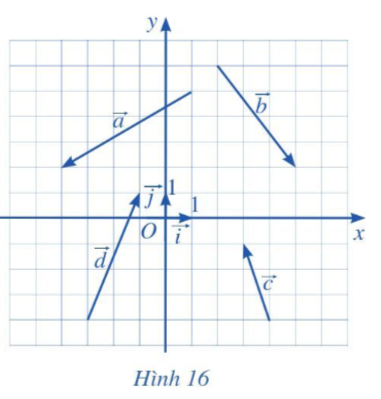
B. Bài tập
Tìm tọa độ của các vectơ trong Hình 16 và biểu diễn mỗi vectơ đó qua hai vectơ →i và →j.

Câu 10:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A, B (Hình 13).
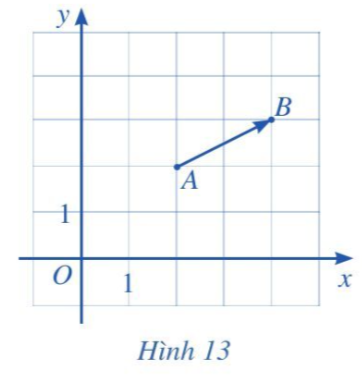
Tìm hoành độ xA và tung độ yA của điểm A; hoành độ xB và tung độ yB của điểm B.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A, B (Hình 13).

Tìm hoành độ xA và tung độ yA của điểm A; hoành độ xB và tung độ yB của điểm B.
Câu 11:
Trong mặt phẳng tọa độ Oxy, cho các điểm:
A(1; 3), B(5; – 1), C(2; – 2), D(– 2; 2).
Chứng minh →AB=→DC.
Trong mặt phẳng tọa độ Oxy, cho các điểm:
A(1; 3), B(5; – 1), C(2; – 2), D(– 2; 2).
Chứng minh →AB=→DC.
Câu 13:
Trong mặt phẳng tọa độ Oxy (Hình 2), hãy:
Tìm hoành độ và tung độ của điểm A.


