Rút gọn biểu thức $A=\frac{\sin \left(-{234}^0\right)-cos{216}^0}{\sin {144}^0-cos{126}^0}.\tan {36}^0$ ta được kết quả:

Đáp án đúng: C

*Lời giải:

$$\begin{gathered} A=\frac{\sin \left(-{234}^0\right)-cos{216}^0}{\sin {144}^0-cos{126}^0}.\tan {36}^0 \\ =\frac{-\sin \left({180}^0+{54}^0\right)-cos\left({180}^0+{36}^0\right)}{\sin \left({180}^0-{36}^0\right)-cos\left({180}^0-{54}^0\right)}.\tan {36}^0 \\ =\frac{\sin {54}^0+cos{36}^0}{\sin {36}^0+cos{54}^0}.\tan {36}^0 \\ =\frac{cos{36}^0+cos{36}^0}{\sin {36}^0+\sin {36}^0}.\tan {36}^0 \\ =\cot {36}^0.\tan {36}^0=1 \end{gathered}$$

*Phương pháp giải:

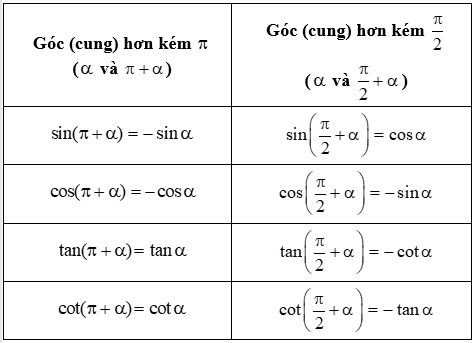
- Sử dụng các góc hơn kém nhau 180 độ để thu gọn giá trị lại

ví dụ: $\sin (-234°) = - \sin (180°+54°) = \sin 54°$

- Biến đổi xong ta sử dụng công thức lượng giác tanxcotx = 1

* Lý thuyết và các dạng bài về giá trị lượng giác của một cung:

Các công thức lượng giác cơ bản:

CÁC DẠNG BÀI:

Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị

Phương pháp giải:

Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.

Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác

Phương pháp giải:

Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.

Ta lựa chọn một trong các cách biến đổi sau:

* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)

* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.

* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.

Dạng 3: Rút gọn biểu thức lượng giác

Phương pháp giải:

Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.

Xem thêm các bài viết liên quan hay, chi tiết:

Giá trị lượng giác của cung và cách giải bài tập (2024) chi tiết nhất 

Trắc nghiệm Giá trị lượng giác của một cung (có đáp án) 

Vở bài tậpToán 10 Bài 2: Giá trị lượng giác của một cung