Phương trình nào sau đây là phương trình đường tròn?

Đáp án đúng là: B

Lời giải

Phương trình đường tròn có dạng: x² + y² – 2ax – 2by + c = 0 (a² + b² – c > 0).

Ta thấy phương trình ở phương án A, D không có dạng trên nên 2 phương trình đó không phải là phương trình đường tròn.

Do đó ta loại phương án A, D.

⦁ Ta có 3x² + 3y² – 3x + 3y + 12 = 0.

⇔ x² + y² – x + 3y + 4 = 0.

Ta có: \(\left\{ \begin{array}{l} - 2a = - 1\\ - 2b = 3\\c = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = - \frac{3}{2}\\c = 4\end{array} \right.\)

Suy ra \({a^2} + {b^2} - c = {\left( {\frac{1}{2}} \right)^2} + {\left( { - \frac{3}{2}} \right)^2} - 4 = - \frac{3}{2} < 0\).b

Do đó phương trình ở phương án C không phải là phương trình đường tròn.

Vì vậy ta loại phương án C.

⦁ Ta có 2x² + 2y² – 2y = 0.

⇔ x² + y² – y = 0.

Ta có: \(\left\{ \begin{array}{l} - 2a = 0\\ - 2b = - 1\\c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = \frac{1}{2}\\c = 0\end{array} \right.\)

Suy ra \({a^2} + {b^2} - c = {0^2} + {\left( {\frac{1}{2}} \right)^2} - 0 = \frac{1}{4} > 0\).

Do đó phương trình ở phương án B là phương trình đường tròn.

Vậy ta chọn phương án B.

*Phương pháp giải:

Phương trình đường tròn có dạng $x^2+y^2-2ax-2by+c=0$ với các số $a,b,c$ thỏa mãn điều kiện $a^2+b^2>c$

*Lý thuyết:

Trong mặt phẳng Oxy cho đường tròn (C) tâm I(a; b), bán kính R. Ta có phương trình đường tròn: ${(x-a)}^2+{(y-b)}^2=R^2$

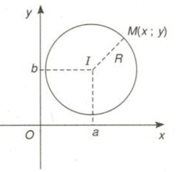
- Nhận xét:

+ Phương trình đường tròn ${(x-a)}^2+{(y-b)}^2=R^2$ có thể được viết dưới dạng $x^2+y^2-2ax-2by+c=0$ trong đó $c=a^2+b^2-R^2$

+ Ngược lại, phương trình $x^2+y^2-2ax-2by+c=0$ là phương trình đường tròn khi và chỉ khi $a^2+b^2-c>0$. Khi đó đường tròn có tâm I(a; b) và bán kính $R=\sqrt{a^2+b^2-c}$

Xem thêm

Phương trình đường tròn (lý thuyết và cách giải các dạng bài tập) 

Trắc nghiệm Phương trình đường tròn có đáp án – Toán lớp 10