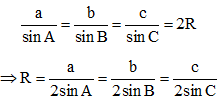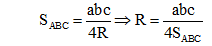Một tam giác có ba cạnh là 52; 56; 60. Bán kính đường tròn ngoại tiếp là:

Đáp án đúng là: A

*Phương pháp giải:

- Sử dụng công thức Hê-rông để tính diện tích tam giác do đã biết độ dài 3 cạnh của tam giác.

- Công thức Hê-rông: $S=\sqrt{p(p-a)(p-b)(p-c)}$

- Sử dụng công thức$S=\frac{abc}{4R}\Rightarrow R=\frac{abc}{4S}$ để tính được bán kính khi đã biết độ dài 3 cạnh và diện tích của tam giác.

*Lời giải

Ta có:  Nửa chu vi của tam giác đã cho: 

$$\begin{gathered} p=\frac{a+b+c}{2} \\ =\frac{52+56+60}{2}=84. \end{gathered}$$

Suy ra: 

$$\begin{gathered} S=\sqrt{p(p-a)(p-b)(p-c)} \\ =\sqrt{84(84-52)(84-56)(84-60)} \\ =1344 \end{gathered}$$

Mà $S=\frac{abc}{4R}$

$$\begin{gathered} \Rightarrow R=\frac{abc}{4S} \\ =\frac{\mathrm{52.56.60}}{4.1344}=\frac{65}{2} \end{gathered}$$

* Một số phương pháp giải bài toán liên quan đến tính bán kính đường tròn ngoại tiếp

Phương pháp 1: Sử dụng đinh lý sin trong tam giác

Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:

Phương pháp 2: Sử dụng diện tích tam giác

        $p=\frac{a+b+c}{2}$ là nửa chu vi 

       $S_{ABC}=\sqrt{p(p-a)(p-b)(p-c)}$    (Công thức Hê-rông) 

Phương pháp 3: Sử dụng trong hệ tọa độ

- Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC

- Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có)

- Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm

 R = OA = OB = OC.

Phương pháp 4: Sử dụng trong tam giác vuông (kiến thức lớp 9)

Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền, do đó bán kính đường tròn ngoại tiếp tam giác vuông chính bằng nửa độ dài cạnh huyền.

$\to$Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.

Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án)

Tóm tắt lý thuyết Toán lớp 10 Chương 3. Hệ thức lượng trong tam giác - Kết nối tri thức