Câu hỏi:
21/07/2024 115
Hàm số y = –x2 + 2x + 3 có đồ thị là hình nào trong các hình sau?
A.
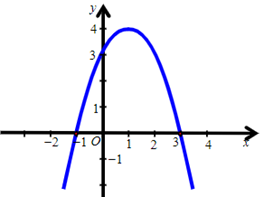

B.
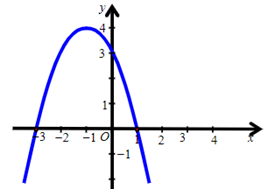

C.
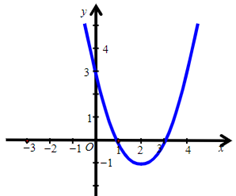

D.

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Cách 1:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 2, c = 3.
Ta có ∆ = b2 – 4ac = 4 – 4.(–1).3 = 16.
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 + 2x + 3 là một parabol (P):
⦁ Đỉnh S có tọa độ: xS=−b2a=−22.(−1)=1 và yS=−Δ4a=−164.(−1)=4.
Suy ra tọa độ đỉnh S(1; 4).
⦁ Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy).
⦁ Có bề lõm quay xuống dưới vì a = –1 < 0.
⦁ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ngoài ra, phương trình –x2 + 2x + 3 = 0 có hai nghiệm phân biệt x1 = 3 và x2 = –1 nên đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có tọa độ (3; 0) và (–1; 0).
Ta vẽ được đồ thị sau:
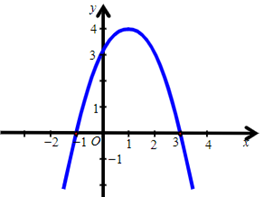
Vậy ta chọn phương án A.
Cách 2:
• Xét hàm số y = –x2 + 2x + 3 có a = –1, b = 2, c = 3.
Vì a = –1 < 0 nên đồ thị có bề lõm quay xuống dưới.
Do đó ta loại phương án C.
• Đỉnh S có tọa độ: xS=−b2a=−22.(−1)=1 và yS=−Δ4a=−164.(−1)=4.
Suy ra tọa độ đỉnh S(1; 4).
Do đó ta loại phương án B và D.
Vậy ta chọn phương án A.
Hướng dẫn giải
Đáp án đúng là: A
Cách 1:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 2, c = 3.
Ta có ∆ = b2 – 4ac = 4 – 4.(–1).3 = 16.
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 + 2x + 3 là một parabol (P):
⦁ Đỉnh S có tọa độ: xS=−b2a=−22.(−1)=1 và yS=−Δ4a=−164.(−1)=4.
Suy ra tọa độ đỉnh S(1; 4).
⦁ Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy).
⦁ Có bề lõm quay xuống dưới vì a = –1 < 0.
⦁ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ngoài ra, phương trình –x2 + 2x + 3 = 0 có hai nghiệm phân biệt x1 = 3 và x2 = –1 nên đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có tọa độ (3; 0) và (–1; 0).
Ta vẽ được đồ thị sau:

Vậy ta chọn phương án A.
Cách 2:
• Xét hàm số y = –x2 + 2x + 3 có a = –1, b = 2, c = 3.
Vì a = –1 < 0 nên đồ thị có bề lõm quay xuống dưới.
Do đó ta loại phương án C.
• Đỉnh S có tọa độ: xS=−b2a=−22.(−1)=1 và yS=−Δ4a=−164.(−1)=4.
Suy ra tọa độ đỉnh S(1; 4).
Do đó ta loại phương án B và D.
Vậy ta chọn phương án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Điều kiện của m để hàm số y = (m – 1)x2 + 2mx – m2 + 4 là hàm số bậc hai là:
Câu 2:
Parabol (P): y = ax2 + 3x – 2 (a ≠ 0) có trục đối xứng là đường thẳng x = –3 là: