Câu hỏi:
25/10/2024 2,022Giả sử CD = h là chiều cao của tháp, trong đó C là chân tháp.
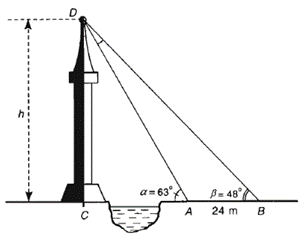
Một người đứng tại vị trí A (\(\widehat {CAD} = 63^\circ ),\) không sang được bờ bên kia để đo chiều cao h của tháp nên chọn thêm một điểm B (ba điểm A, B, C thẳng hàng) cách A một khoảng 24 m và \[\widehat {CBD} = 48^\circ \] để tính toán được chiều cao của tháp. Chiều cao h của tháp gần nhất với:
A. 18 m;
B. 18,5 m;
C. 60 m;
D. 60,5 m.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
* Lời giải:
Ta có \(\widehat {CAD} + \widehat {BAD} = 180^\circ \) (hai góc kề bù).
\( \Rightarrow \widehat {BAD} = 180^\circ - \widehat {CAD} = 180^\circ - 63^\circ = 117^\circ \).
∆ABD có: \(\widehat {BAD} + \widehat {ADB} + \widehat {ABD} = 180^\circ \) (định lí tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {ADB} = 180^\circ - \left( {\widehat {BAD} + \widehat {ABD}} \right) = 180^\circ - \left( {117^\circ + 48^\circ } \right) = 15^\circ \).
Áp dụng định lí sin cho ∆ABD, ta được \(\frac{{BD}}{{\sin \widehat {BAD}}} = \frac{{AB}}{{\sin \widehat {ADB}}}\)
Suy ra \(\frac{{BD}}{{\sin 117^\circ }} = \frac{{24}}{{\sin 15^\circ }}\)
Do đó \(BD = \frac{{24.\sin 117^\circ }}{{\sin 15^\circ }} \approx 82,6\) (m)
∆BCD vuông tại C: \(\sin \widehat {CBD} = \frac{{CD}}{{BD}}\).
Suy ra \(h = CD = BD.\sin \widehat {CBD} \approx 82,6.\sin 48^\circ = 61,4\) (m)
Giá trị này gần với 60,5 m.
* Phương pháp giải:
- sử dụng tổng 3 góc trong 1 tam giác bằng 180 độ và sử udngj định lý sin trong tam giác để tính toán
+ tìm ra số đo góc BAD và từ đó tìm ra số đo góc ADB
+ áp dụng định lý sin vào tam giác ABD để tìm ra độ dài cạnh BD
+ xét tam giác vuông BCD để tính ra cạnh CD=h
* Lý thuyết cần nắm thêm về hệ thức lượng trong tam giác:
Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° ‒ α) = sinα;
cos(180° ‒ α) = ‒cosα;
tan(180° ‒ α) = ‒tanα (α ≠ 90°);
cot(180° ‒ α) = ‒cotα (0° < α < 180°).
Định lí côsin trong tam giác
Định lí côsin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
a2 = b2 + c2 – 2bc.cosA;
b2 = c2 + a2 – 2ca.cosB;
c2 = a2 + b2 – 2ab.cosC.
Từ định lí côsin, ta có hệ quả sau đây:
Hệ quả:
Định lí sin trong tam giác
Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
Trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.
Từ định lí sin, ta có hệ quả sau đây:
Hệ quả:
a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;
Các công thức tính diện tích tam giác
Cho tam giác ABC. Ta kí hiệu:
+) BC = a, CA = b, AB = c.
+) ha, hb, hc là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB.
+) R là bán kính đường tròn ngoại tiếp tam giác.
+) r là bán kính đường tròn nội tiếp tam giác.
+) p là nửa chu vi tam giác.
+) S là diện tích tam giác.
Ta có các công thức tính diện tích tam giác sau:
(1)
(2)
(3)
(4) S = pr;
(5) (Công thức Heron).
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết tổng hợp cuối chương 4 – Toán 10 Chân trời sáng tạo
Sách bài tập Toán 10 (Chân trời sáng tạo): Bài tập cuối chương 4
Trắc nghiệm Ôn tập chương 4 (Chân trời sáng tạo 2024) - Toán 10
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC có a.sinA + b.sinB + c.sinC = ha + hb + hc. Khi đó ∆ABC là:
Câu 2:
Cho ∆ABC và các khẳng định sau:
(I) b2 – c2 = a(b.cosC – c.cosB);
(II) (b + c)sinA = a(sinB + sinC);
(III) ha = 2R.sinB.sinC;
(IV) S = R.r.(sinA + sinB + sin C);
Số khẳng định đúng là:
Cho ∆ABC và các khẳng định sau:
(I) b2 – c2 = a(b.cosC – c.cosB);
(II) (b + c)sinA = a(sinB + sinC);
(III) ha = 2R.sinB.sinC;
(IV) S = R.r.(sinA + sinB + sin C);
Số khẳng định đúng là:
Câu 3:
Từ vị trí A, người ta quan sát một cái cây cao mọc vuông góc với mặt đất như hình vẽ.
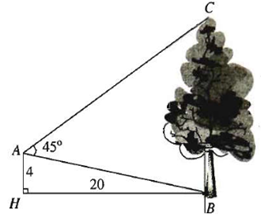
Biết vị trí quan sát cách mặt đất một khoảng AH = 4 m và khoảng cách từ chân đường vuông góc của vị trí quan sát A trên mặt đất tới gốc cây là HB = 20 m, \(\widehat {BAC} = 45^\circ \). Chiều cao của cây gần nhất với giá trị nào sau đây?
Câu 4:
Cho biết tanα = –3 (0° ≤ α ≤ 180°). Giá trị của \(H = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }}\) bằng:
Câu 5:
Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50° và 40° so với phương nằm ngang.
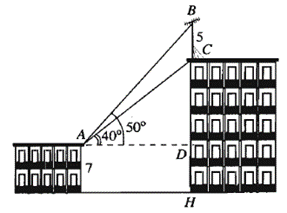
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
Câu 6:
Từ hai vị trí A và B của một tòa nhà, người ta quan sát được đỉnh C của ngọn núi. Biết rằng độ cao của tòa nhà là AB = 70 m, phương nhìn AC tạo với phương ngang AH một góc bằng 30°, phương nhìn BC tạo với phương ngang BD một góc bằng 15°30’.
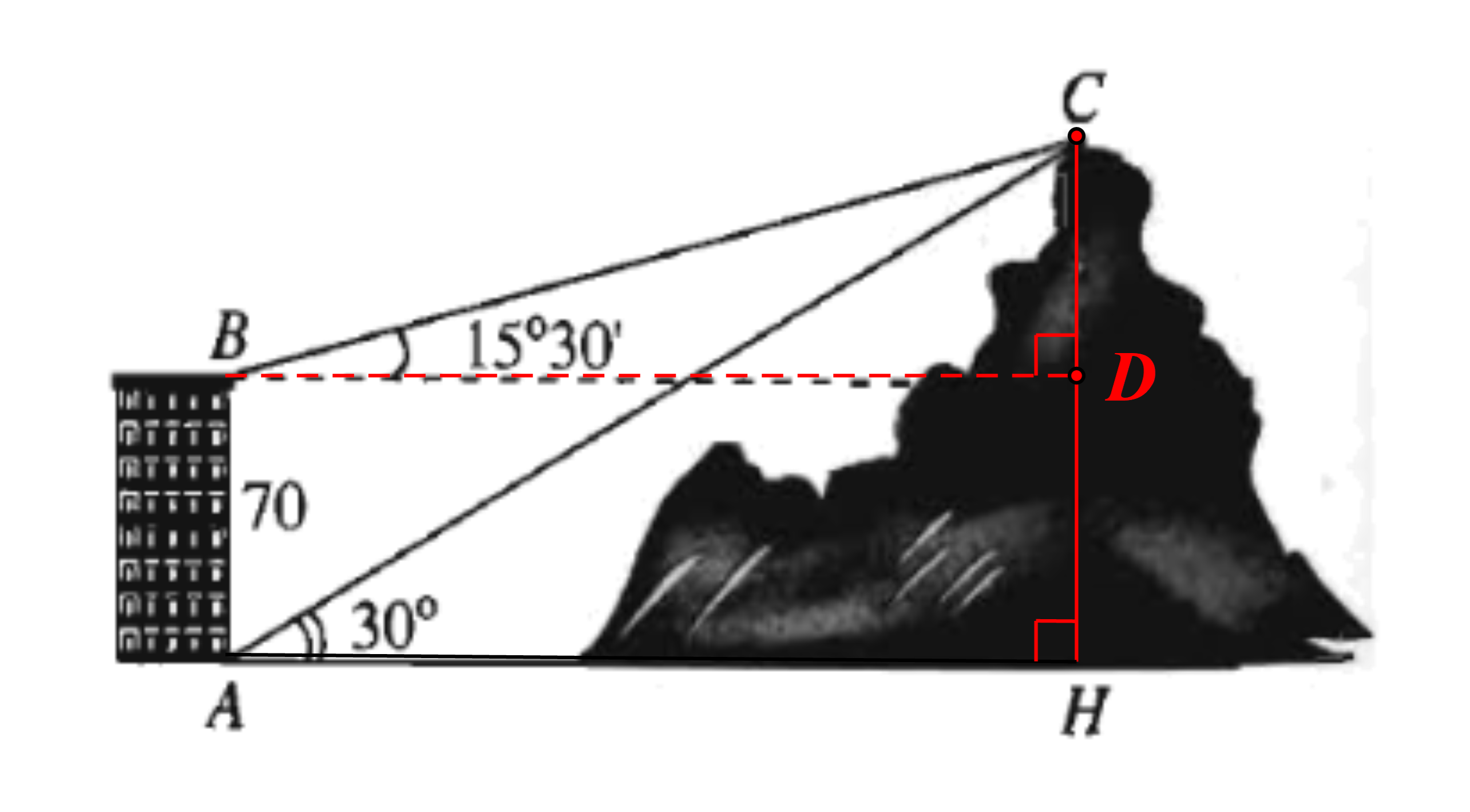
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
Câu 7:
Cho ∆ABC thỏa mãn \[\sin A = \frac{{\sin B + \sin C}}{{\cos B + \cos C}}\]. Khi đó ∆ABC là:
Câu 8:
Cho biết \(2\cos \alpha + \sqrt 2 \sin \alpha = 2\), với 0° < α < 90°. Giá trị của cotα bằng:
Câu 9:
Cho biết sinα – cosα = \(\frac{1}{{\sqrt 5 }}\)(0° ≤ α, β ≤ 180°). Giá trị của \(E = \sqrt {{{\sin }^4}\alpha + {{\cos }^4}\alpha } \) bằng:


