Câu hỏi:
23/11/2024 4,343
Đường tròn (C) có tâm I(2; –3) và tiếp xúc với trục Oy có phương trình là:
Đường tròn (C) có tâm I(2; –3) và tiếp xúc với trục Oy có phương trình là:
A. (x + 2)2 + (y – 3)2 = 4;
A. (x + 2)2 + (y – 3)2 = 4;
B. (x + 2)2 + (y – 3)2 = 9;
B. (x + 2)2 + (y – 3)2 = 9;
C. (x – 2)2 + (y + 3)2 = 4;
C. (x – 2)2 + (y + 3)2 = 4;
D. (x – 2)2 + (y + 3)2 = 9.
D. (x – 2)2 + (y + 3)2 = 9.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Lời giải
Phương trình trục Oy: x = 0.
Đường tròn (C) có tâm I(2; –3) và tiếp xúc với trục Oy nên có bán kính là:
R = d(I, Oy) =
Vậy phương trình đường tròn (C): (x – 2)2 + (y + 3)2 = 4.
*Phương pháp giải:
+ Cho đường tròn ( C) tâm I( a;b) bán kính R và đường thẳng d.
Đường thẳng d tiếp xúc với đường tròn ( C) khi và chỉ khi : d(I, d)= R
+ Trục tung có phương trình x= 0 nên để đường tròn tiếp xúc với trục tung khi và chỉ khi:
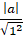 = R hay R = |a|
= R hay R = |a|
*Lý thuyết:
1. Phương trình đường tròn
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
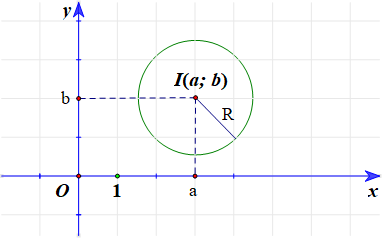 Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạo
Đáp án đúng là: C
Lời giải
Phương trình trục Oy: x = 0.
Đường tròn (C) có tâm I(2; –3) và tiếp xúc với trục Oy nên có bán kính là:
R = d(I, Oy) =
Vậy phương trình đường tròn (C): (x – 2)2 + (y + 3)2 = 4.
*Phương pháp giải:
+ Cho đường tròn ( C) tâm I( a;b) bán kính R và đường thẳng d.
Đường thẳng d tiếp xúc với đường tròn ( C) khi và chỉ khi : d(I, d)= R
+ Trục tung có phương trình x= 0 nên để đường tròn tiếp xúc với trục tung khi và chỉ khi:
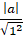
*Lý thuyết:
1. Phương trình đường tròn
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
 Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạoCÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Đường tròn (C): x2 + y2 – 6x + 2y + 6 = 0 có tâm I và bán kính R là:
Đường tròn (C): x2 + y2 – 6x + 2y + 6 = 0 có tâm I và bán kính R là:
Câu 2:
Cho đường tròn (C): (x – 2)2 + (y + 4)2 = 25, biết tiếp tuyến vuông góc với đường thẳng d: 3x – 4y + 5 = 0. Phương trình tiếp tuyến của (C) là:
Cho đường tròn (C): (x – 2)2 + (y + 4)2 = 25, biết tiếp tuyến vuông góc với đường thẳng d: 3x – 4y + 5 = 0. Phương trình tiếp tuyến của (C) là:
Câu 3:
Tọa độ tâm I và bán kính R của đường tròn (C): 16x2 + 16y2 + 16x – 8y – 11 = 0 là:
Tọa độ tâm I và bán kính R của đường tròn (C): 16x2 + 16y2 + 16x – 8y – 11 = 0 là:
Câu 4:
Cho đường tròn (C): x2 + y2 + 5x + 7y – 3 = 0. Khoảng cách từ tâm của (C) đến trục hoành bằng:
Cho đường tròn (C): x2 + y2 + 5x + 7y – 3 = 0. Khoảng cách từ tâm của (C) đến trục hoành bằng:
Câu 5:
Cho phương trình (C): x2 + y2 – 2(m + 1)x + 4y – 1 = 0. Với giá trị nào của m thì đường tròn (C) có bán kính nhỏ nhất?
Cho phương trình (C): x2 + y2 – 2(m + 1)x + 4y – 1 = 0. Với giá trị nào của m thì đường tròn (C) có bán kính nhỏ nhất?
Câu 6:
Đường tròn (C) có tâm I(1; –5) và đi qua O(0; 0) có phương trình là:
Đường tròn (C) có tâm I(1; –5) và đi qua O(0; 0) có phương trình là:
Câu 7:
Đường tròn (C) đi qua hai điểm A(–1; 2), B(–2; 3) và có tâm I thuộc đường thẳng ∆: 3x – y + 10 = 0. Phương trình đường tròn (C) là:
Đường tròn (C) đi qua hai điểm A(–1; 2), B(–2; 3) và có tâm I thuộc đường thẳng ∆: 3x – y + 10 = 0. Phương trình đường tròn (C) là:
Câu 8:
Tọa độ tâm I của đường tròn đi qua ba điểm A(0; 4), B(2; 4), C(4; 0) là:
Tọa độ tâm I của đường tròn đi qua ba điểm A(0; 4), B(2; 4), C(4; 0) là:
Câu 9:
Cho đường tròn (C): x2 + y2 – 2x – 4y + 1 = 0. Gọi d1, d2 lần lượt là tiếp tuyến của đường tròn (C) tại điểm M(3; 2), N(1; 0). Tọa độ giao điểm của d1 và d2 là:
Cho đường tròn (C): x2 + y2 – 2x – 4y + 1 = 0. Gọi d1, d2 lần lượt là tiếp tuyến của đường tròn (C) tại điểm M(3; 2), N(1; 0). Tọa độ giao điểm của d1 và d2 là:
Câu 10:
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
Câu 11:
Đường tròn (C) có tâm I thuộc đường thẳng d: x + 3y + 8 = 0, đi qua điểm A(–2; 1) và tiếp xúc với đường thẳng ∆: 3x – 4y + 10 = 0. Phương trình đường tròn (C) là:
Đường tròn (C) có tâm I thuộc đường thẳng d: x + 3y + 8 = 0, đi qua điểm A(–2; 1) và tiếp xúc với đường thẳng ∆: 3x – 4y + 10 = 0. Phương trình đường tròn (C) là:
Câu 12:
Tọa độ tâm I và bán kính R của đường tròn (C): (x – 1)2 + (y + 3)2 = 16 là:
Tọa độ tâm I và bán kính R của đường tròn (C): (x – 1)2 + (y + 3)2 = 16 là:
Câu 13:
Đường tròn (C): x2 + y2 + 12x – 14y + 4 = 0 viết được dưới dạng:
Đường tròn (C): x2 + y2 + 12x – 14y + 4 = 0 viết được dưới dạng:
Câu 14:
Cho phương trình x2 + y2 – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:
Cho phương trình x2 + y2 – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:


