Câu hỏi:
23/11/2024 9,188
Đường tròn (C) có tâm I (1; -5) và đi qua O (0; 0) có phương trình là:
Đường tròn (C) có tâm I (1; -5) và đi qua O (0; 0) có phương trình là:
A. \[{\left( {x + 1} \right)^2} + {\left( {y - 5} \right)^2} = 26;\]
A. \[{\left( {x + 1} \right)^2} + {\left( {y - 5} \right)^2} = 26;\]
B. \[{\left( {x + 1} \right)^2} + {\left( {y - 5} \right)^2} = \sqrt {26} ;\]
B. \[{\left( {x + 1} \right)^2} + {\left( {y - 5} \right)^2} = \sqrt {26} ;\]
C. \[{\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 26;\]
C. \[{\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 26;\]
D. \[{\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = \sqrt {26} .\]
D. \[{\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = \sqrt {26} .\]
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Lời giải
Ta có: Bán kính của đường tròn R = OI = \[\sqrt {{{(1 - 0)}^2} + {{( - 5 - 0)}^2}} = \sqrt {26} \]
Phương trình đường tròn\[\left( C \right):\left\{ \begin{array}{l}I\left( {1; - 5} \right)\\R = OI = \sqrt {26} \end{array} \right.\] là: \[{\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 26\]
*Phương pháp giải:
+ Cho đường tròn ( C) tâm I( a;b) bán kính R và đường thẳng d.
Đường thẳng d tiếp xúc với đường tròn ( C) khi và chỉ khi : d(I, d)= R
Viết phương trình đường tròn
*Lý thuyết:
1. Phương trình đường tròn
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
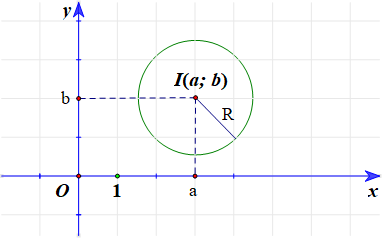Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạo
Đáp án đúng là: C
Lời giải
Ta có: Bán kính của đường tròn R = OI = \[\sqrt {{{(1 - 0)}^2} + {{( - 5 - 0)}^2}} = \sqrt {26} \]
Phương trình đường tròn\[\left( C \right):\left\{ \begin{array}{l}I\left( {1; - 5} \right)\\R = OI = \sqrt {26} \end{array} \right.\] là: \[{\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 26\]
*Phương pháp giải:
+ Cho đường tròn ( C) tâm I( a;b) bán kính R và đường thẳng d.
Đường thẳng d tiếp xúc với đường tròn ( C) khi và chỉ khi : d(I, d)= R
Viết phương trình đường tròn
*Lý thuyết:
1. Phương trình đường tròn
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạoCÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Viết phương trình tiếp tuyến của đường tròn \[\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 5\], biết tiếp tuyến song song với đường thẳng d: 2x + y + 7 = 0.
Viết phương trình tiếp tuyến của đường tròn \[\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 5\], biết tiếp tuyến song song với đường thẳng d: 2x + y + 7 = 0.
Câu 3:
Đường tròn đường kính AB với A (3; -1), B (1; -5) có phương trình là:
Đường tròn đường kính AB với A (3; -1), B (1; -5) có phương trình là:
Câu 4:
Đường tròn (C) có tâm I (-2; 3) và đi qua M (2; -3) có phương trình là:
Đường tròn (C) có tâm I (-2; 3) và đi qua M (2; -3) có phương trình là:
Câu 5:
Phương trình tiếp tuyến d của đường tròn \[\left( C \right):{x^2} + {y^2} - 3x - y = 0\] tại điểm đối xứng với M (-1; -1) qua trục Oy là:
Phương trình tiếp tuyến d của đường tròn \[\left( C \right):{x^2} + {y^2} - 3x - y = 0\] tại điểm đối xứng với M (-1; -1) qua trục Oy là:
Câu 6:
Gọi I và R lần lượt là tâm và bán kính của đường tròn \[\left( C \right):{x^2} + {y^2} = 9\]. Tìm I và tính S = \[{R^3}\].
Gọi I và R lần lượt là tâm và bán kính của đường tròn \[\left( C \right):{x^2} + {y^2} = 9\]. Tìm I và tính S = \[{R^3}\].
Câu 7:
Gọi I(a; b) là tâm của đường tròn \[\left( C \right):{x^2} + {\left( {y + 4} \right)^2} = 5\]. Tính S = 2a + b:
Gọi I(a; b) là tâm của đường tròn \[\left( C \right):{x^2} + {\left( {y + 4} \right)^2} = 5\]. Tính S = 2a + b:
Câu 8:
Đường tròn có tâm trùng với gốc tọa độ, bán kính R = 1 có phương trình là:
Đường tròn có tâm trùng với gốc tọa độ, bán kính R = 1 có phương trình là:
Câu 9:
Đường tròn \[\left( C \right):{x^2} + {y^2} - 6x + 2y + 6 = 0\] có tâm I, bán kính R lần lượt là:
Đường tròn \[\left( C \right):{x^2} + {y^2} - 6x + 2y + 6 = 0\] có tâm I, bán kính R lần lượt là:
Câu 10:
Viết phương trình tiếp tuyến của đường tròn \[\left( C \right):{x^2} + {y^2} + 4x + 4y - 17 = 0\], biết tiếp tuyến song song với đường thẳng d: 3x – 4y – 2018 = 0.
Câu 11:
Cho đường tròn \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 8\]. Viết phương trình tiếp tuyến d của (C) tại điểm A (3; -4).
Cho đường tròn \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 8\]. Viết phương trình tiếp tuyến d của (C) tại điểm A (3; -4).
Câu 12:
Tọa độ tâm I và bán kính R của đường tròn \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 16\] là:
Tọa độ tâm I và bán kính R của đường tròn \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 16\] là:
Câu 13:
Phương trình tiếp tuyến d của đường tròn \[\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\] tại trung điểm của A (1; 3) và B (3; -1) là:
Phương trình tiếp tuyến d của đường tròn \[\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\] tại trung điểm của A (1; 3) và B (3; -1) là:
Câu 14:
Gọi I và R lần lượt là tâm và bán kính của đường tròn \[\left( C \right):{\left( {x + 1} \right)^2} + {y^2} = 8\]. Tìm I và tính S = 3.R.
Gọi I và R lần lượt là tâm và bán kính của đường tròn \[\left( C \right):{\left( {x + 1} \right)^2} + {y^2} = 8\]. Tìm I và tính S = 3.R.
