Trắc nghiệm Toán 10 Bài 21. Đường tròn trong mặt phẳng toạ độ có đáp án
-
317 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Tọa độ tâm I và bán kính R của đường tròn \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 16\] là:
Xem đáp án
Đáp án đúng là: B
Ta có: \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 16\]\[ \Rightarrow \]Tâm I (1; -3), bán kính R = \[\sqrt {16} \]= 4.
Câu 2:
21/07/2024Gọi I(a; b) là tâm của đường tròn \[\left( C \right):{x^2} + {\left( {y + 4} \right)^2} = 5\]. Tính S = 2a + b:
Xem đáp án
Đáp án đúng là: D
Ta có: \[\left( C \right):{x^2} + {\left( {y + 4} \right)^2} = 5\]
⇒ a = 0, b = -4
⇒ S = 2a + b = 2.0 + (-4) = -4.
Câu 3:
17/07/2024Gọi I và R lần lượt là tâm và bán kính của đường tròn \[\left( C \right):{\left( {x + 1} \right)^2} + {y^2} = 8\]. Tìm I và tính S = 3.R.
Xem đáp án
Đáp án đúng là: C
Ta có: \[\left( C \right):{\left( {x + 1} \right)^2} + {y^2} = 8 \Rightarrow \] \[I\left( { - 1;0} \right),\,R = \sqrt 8 = 2\sqrt 2 \].
3.R = 6\[\sqrt 2 \].
Câu 4:
21/07/2024Gọi I và R lần lượt là tâm và bán kính của đường tròn \[\left( C \right):{x^2} + {y^2} = 9\]. Tìm I và tính S = \[{R^3}\].
Xem đáp án
Đáp án đúng là: D
Ta có: \(\left( C \right):{x^2} + {y^2} = 9\)\( \Rightarrow I\left( {0;0} \right),\,\,R = \sqrt 9 = 3.\)
Suy ra S = \[{R^3}\]= 27.
Câu 5:
21/07/2024Đường tròn \[\left( C \right):{x^2} + {y^2} - 6x + 2y + 6 = 0\] có tâm I, bán kính R lần lượt là:
Xem đáp án
Đáp án đúng là: C
Ta có: \[\left( C \right):{x^2} + {y^2} - 6x + 2y + 6 = 0\]\[ \Rightarrow a = \frac{{ - 6}}{{ - 2}} = 3\]; \[b = \frac{2}{{ - 2}} = - 1\]; c = 6
\[ \Rightarrow \]I (3; -1) và \[R = \sqrt {{3^2} + {{\left( { - 1} \right)}^2} - 6} = \]2.
Câu 6:
17/07/2024Đường tròn có tâm trùng với gốc tọa độ, bán kính R = 1 có phương trình là:
Xem đáp án
Đáp án đúng là: B
Đường tròn (C) phải thoả mãn hai điều kiện sau:
\[\left( C \right):\left\{ \begin{array}{l}I\left( {0;0} \right)\\R = 1\end{array} \right.\] suy ra chỉ có phương trình \[{x^2} + {y^2} = 1\] thoả mãn yêu cầu.
Câu 7:
18/11/2024Đường tròn có tâm I (1; 2), bán kính R = 3 có phương trình là:
Xem đáp án
Đáp án đúng là: A
Lời giải
Đường tròn có tâm I (1; 2), bán kính R = 3 có phương trình là:
\[{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\]
\[ \Leftrightarrow {x^2} + {y^2} - 2x - 4y - 4 = 0\]
*Phương pháp giải:
Phương trình đường tròn có dạng với các số thỏa mãn điều kiện
*Lý thuyết:
Trong mặt phẳng Oxy cho đường tròn (C) tâm I(a; b), bán kính R. Ta có phương trình đường tròn:
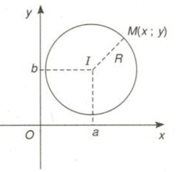
- Nhận xét:
+ Phương trình đường tròn có thể được viết dưới dạng trong đó
+ Ngược lại, phương trình là phương trình đường tròn khi và chỉ khi . Khi đó đường tròn có tâm I(a; b) và bán kính
Xem thêm
Phương trình đường tròn (lý thuyết và cách giải các dạng bài tập)
Câu 8:
23/11/2024Đường tròn (C) có tâm I (1; -5) và đi qua O (0; 0) có phương trình là:
Xem đáp án
Đáp án đúng là: C
Lời giải
Ta có: Bán kính của đường tròn R = OI = \[\sqrt {{{(1 - 0)}^2} + {{( - 5 - 0)}^2}} = \sqrt {26} \]
Phương trình đường tròn\[\left( C \right):\left\{ \begin{array}{l}I\left( {1; - 5} \right)\\R = OI = \sqrt {26} \end{array} \right.\] là: \[{\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 26\]
*Phương pháp giải:
+ Cho đường tròn ( C) tâm I( a;b) bán kính R và đường thẳng d.
Đường thẳng d tiếp xúc với đường tròn ( C) khi và chỉ khi : d(I, d)= R
Viết phương trình đường tròn
*Lý thuyết:
1. Phương trình đường tròn
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
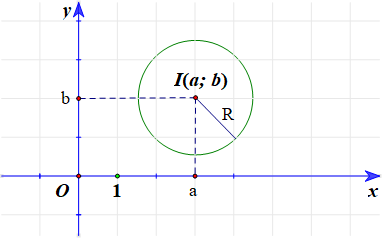Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạoCâu 9:
22/07/2024Đường tròn (C) có tâm I (-2; 3) và đi qua M (2; -3) có phương trình là:
Xem đáp án
Đáp án đúng là: D
Ta có: Bán kính của đường tròn:
R = IM = \[\sqrt {{{\left( {2 + 2} \right)}^2} + {{\left( { - 3 - 3} \right)}^2}} = \sqrt {52} \]
Vậy phương trình đường tròn \[\left( C \right):\left\{ \begin{array}{l}I\left( { - 2;3} \right)\\R = \sqrt {52} \end{array} \right.\]là: \[\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y - 3} \right)^2} = 52.\]
hay \[\left( C \right):{x^2} + {y^2} + 4x - 6y - 39 = 0\].
Câu 10:
21/07/2024Đường tròn đường kính AB với A (3; -1), B (1; -5) có phương trình là:
Xem đáp án
Đáp án đúng là: D
Đường tròn có đường kính AB nên tâm I của đường tròn là trung điểm của AB:
\( \Rightarrow \left\{ \begin{array}{l}{x_I} = \frac{{3 + 1}}{2} = 2\\{y_I} = \frac{{ - 1 + \left( { - 5} \right)}}{2} = - 3\end{array} \right.\)
Và bán kính của đường tròn là:
R = \[\frac{1}{2}AB\] = \[\frac{1}{2}\sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( { - 5 + 1} \right)}^2}} \]= \[\sqrt 5 \]
Khi đó phương trình đường tròn\[\left( C \right):\left\{ \begin{array}{l}I\left( {2; - 3} \right)\\R = \sqrt 5 \end{array} \right.\] là:
\[\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 5.\]
Câu 11:
21/07/2024Phương trình tiếp tuyến d của đường tròn \[\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\] tại trung điểm của A (1; 3) và B (3; -1) là:
Xem đáp án
Đáp án đúng là: D
Gọi M là trung điểm của A và B, ta có: M \[\left( {\frac{{1 + 3}}{2};\frac{{3 + ( - 1)}}{2}} \right)\]= (2; 1).
Đường tròn (C) có tâm I (-2; -2) nên tiếp tuyến tại M có VTPT là \[\vec n = \overrightarrow {IM} = \left( {4;3} \right)\] nên có phương trình là: 4.(x – 2) + 3.(y – 1) = 0\[ \Leftrightarrow \]4x + 3y – 11 = 0.
Câu 12:
16/07/2024Cho đường tròn \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 8\]. Viết phương trình tiếp tuyến d của (C) tại điểm A (3; -4).
Xem đáp án
Đáp án đúng là: C
Đường tròn (C) có tâm I (1; -2) nên tiếp tuyến tại A có VTPT là
\[\vec n = \overrightarrow {IA} = \](2; -2) = 2(1; -1)
Nên có phương trình là: 1(x - 3) - 1.(y + 4) = 0\[ \Leftrightarrow \]x - y - 7 = 0.
Câu 13:
21/07/2024Phương trình tiếp tuyến d của đường tròn \[\left( C \right):{x^2} + {y^2} - 3x - y = 0\] tại điểm đối xứng với M (-1; -1) qua trục Oy là:
Xem đáp án
Đáp án đúng là: D
Gọi N là điểm đối xứng của M qua Oy, ta có: N (1; -1).
Đường tròn (C) có tâm \[I\left( {\frac{3}{2};\frac{1}{2}} \right)\] nên tiếp tuyến tại N có VTPT là
\[\vec n = \overrightarrow {IN} = \left( { - \frac{1}{2}; - \frac{3}{2}} \right) = - \frac{1}{2}\left( {1;3} \right),\]
Nên có phương trình là: 1(x - 1) +3(y + 1) = 0\[ \Leftrightarrow \]x + 3y + 2 = 0.
Câu 14:
21/07/2024Viết phương trình tiếp tuyến của đường tròn \[\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 5\], biết tiếp tuyến song song với đường thẳng d: 2x + y + 7 = 0.
Xem đáp án
Đáp án đúng là: B
Đường tròn (C) có tâm I(3; -1), R = \[\sqrt 5 \].
Vì tiếp tuyến của đường tròn (C) song song với đường thẳng d: 2x + y + 7 = 0 nên tiếp tuyến có dạng \[\Delta \]: 2x + y + c = 0 (c ≠ 7).
Ta có:
Bán kính của đường tròn \[R = d\left( {I;\Delta } \right) \Leftrightarrow \]\[\frac{{\left| {c + 5} \right|}}{{\sqrt 5 }} = \sqrt 5 \]
\[ \Leftrightarrow \]\[\left| {c + 5} \right| = 5\]\[ \Leftrightarrow \]\[\left[ \begin{array}{l}c + 5 = 5\\c + 5 = - 5\end{array} \right.\]
\[ \Leftrightarrow \left[ \begin{array}{l}c = 0\\c = - 10\end{array} \right.\]
suy ra\[\Delta \]:2x + y = 0 hoặc \[\Delta \]:2x + y – 10 = 0.
Câu 15:
21/07/2024Viết phương trình tiếp tuyến của đường tròn \[\left( C \right):{x^2} + {y^2} + 4x + 4y - 17 = 0\], biết tiếp tuyến song song với đường thẳng d: 3x – 4y – 2018 = 0.
Xem đáp án
Đáp án đúng là: A
Ta có: Đường tròn (C) có tâm I(-2; -2), R = 5 và tiếp tuyến có dạng
\[\Delta \]: 3x – 4y + c = 0 (c ≠ -2018)
Bán kính đường tròn: \[R = d\left( {I;\Delta } \right)\] \[ \Leftrightarrow \frac{{\left| {c + 2} \right|}}{5} = 5\]
\[ \Leftrightarrow \left| {c + 2} \right| = 25\]\[ \Leftrightarrow \left[ \begin{array}{l}c + 2 = 25\\c + 2 = - 25\end{array} \right.\]\[ \Leftrightarrow \left[ \begin{array}{l}c = 23\\c = - 27\end{array} \right.\]
suy ra: \[\Delta \]:3x – 4y + 23 = 0 hoặc \[\Delta \]: 3x – 4y – 27 = 0.