Câu hỏi:
18/07/2024 416Cho tam giác ABC vuông cân tại C; AB=√2. Tính |→AB+→AC|
A. √5
B. 5
C. 1
D. √3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
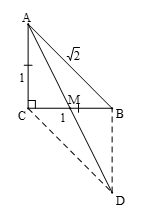
Gọi M là trung điểm của BC, D là điểm đối xứng với A qua M. Suy ra ABDC là bình hành.
Xét ΔABC vuông cân tại C, ta có: AC=BC=1.
⇒CM=BM=12
Xét ΔACM vuông tại C, ta có: AM=√1+14=√52.
Khi đó ta có:
|→AB+→AC|=|→AD|=|2→AM|=2.√52=√5.
Đáp án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho AD và BE là hai phân giác trong của tam giác ABC. Biết AB= 4, BC= 5 và CA= 6. Khi đó →DE bằng:
Câu 3:
Cho tam giác ABC với phân giác trong AD. Biết AB= 5; BC= 6; CA= 7. Khi đó bằng
Câu 7:
Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho . Gọi H là hình chiếu của M lên AB. Tính độ dài lớn nhất của MH?
Câu 10:
Cho I; J; K lần lượt là trung điểm của các cạnh AB; BC; CA của tam giác ABC. Giả sử M là điểm thỏa mãn điều kiện . Khi đó vị trí điểm M là:
Câu 13:
Cho hai điểm cố định A; B. gọi I là trung điểm của AB. Tập hợp các điểm M thoả: là:
Câu 15:
Trên trục cho 3 điểm A; B; C có tọa độ lần lượt là a; b;c . Tìm điểm I sao cho


