Câu hỏi:
03/07/2024 177
Cho tam giác ABC. Trên cạnh AB, AC lần lượt lấy hai điểm M, N. Khẳng định nào sau đây là đúng?
A. \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AB}}.\frac{{AN}}{{AC}}\);
Đáp án chính xác
B. \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AC}}{{AB}}.\frac{{AN}}{{AM}}\);
C. \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AB}}{{AM}}.\frac{{AN}}{{AC}}\);
D. \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{MN}}{{AB}}.\frac{{AN}}{{AC}}\).
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A.
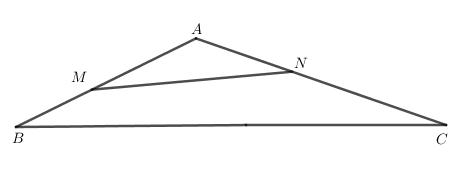
Diện tích tam giác AMN là: \({S_{AMN}} = \frac{1}{2}.AM.AN.\sin \widehat {MAN}\).
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \widehat {BAC}\).
Do \(\widehat {MAN} = \widehat {BAC}\) (hai góc trùng nhau)
Nên \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AB}}.\frac{{AN}}{{AC}}\).
Hướng dẫn giải:
Đáp án đúng là: A.
Diện tích tam giác AMN là: \({S_{AMN}} = \frac{1}{2}.AM.AN.\sin \widehat {MAN}\).
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \widehat {BAC}\).
Do \(\widehat {MAN} = \widehat {BAC}\) (hai góc trùng nhau)
Nên \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AB}}.\frac{{AN}}{{AC}}\).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC có BC = a, AC = b, AB = c. Khẳng định nào sau đây là đúng?
Xem đáp án »
23/07/2024
6,890
Câu 2:
Cho tam giác ABC có BC = a, AC = b, AB = c và b – c = \(\frac{a}{2}\). Khẳng định nào sau đây là đúng?
Xem đáp án »
15/07/2024
335
Câu 3:
Cho tam giác ABC có BC = a, AC = b, AB = c và bán kính đường tròn ngoại tiếp bằng R. Khẳng định nào sau đây là đúng?
Xem đáp án »
21/07/2024
190
Câu 4:
Cho tam giác ABC thỏa mãn sin2A = sinB.sinC. Khẳng định nào sau đây là đúng?
Xem đáp án »
17/07/2024
174
Câu 5:
Cho tam giác ABC có BC = a, AC = b, AB = c và b + c = 2a. Khẳng định nào sau đây là đúng?
Xem đáp án »
03/07/2024
154
Câu 6:
Cho tam giác ABC. Với S là diện tích tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác, khẳng định nào sau đây là đúng?
Xem đáp án »
18/07/2024
143
Câu 8:
Tam giác ABC có BC = a, CA = b, AB = c.
Chứng minh rằng: a = b.cos C + c.cos B.
Tam giác ABC có BC = a, CA = b, AB = c.
Chứng minh rằng: a = b.cos C + c.cos B.
Xem đáp án »
03/07/2024
134
Câu 9:
Tam giác ABC có BC = a, CA = b, AB = c và \({a^2} = 2\left( {{b^2} - {c^2}} \right)\). Chứng minh rằng: \({\sin ^2}A = 2\left( {{{\sin }^2}B - {{\sin }^2}C} \right)\).
Xem đáp án »
03/07/2024
125
