Câu hỏi:
10/12/2024 2,531Cho tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I. Khi đó
A. I cách đều ba đỉnh của tam giác ABC
B. IC = ID = IB = IE
C. I là điểm cách đều ba cạnh của tam giác ABC
D. Cả A, B đều đúng
Trả lời:
Giải bởi Vietjack
Đáp án đúng là : C
Lời giải
Tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I nên II là điểm cách đều ba cạnh của tam giác ABC.
*Phương pháp giải:
Sử dụng định lí về tính chất ba đường phân giác của tam giác: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
*Lý thuyết:
1. Đường phân giác của tam giác
– Trong tam giác ABC (hình vẽ bên dưới), tia phân giác của cắt cạnh BC tại D. Khi đó, đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.
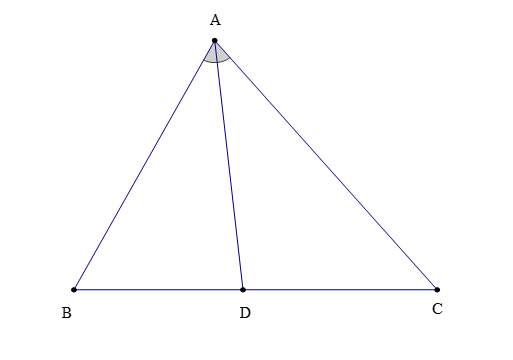
Đôi khi, đường thẳng AD cũng được gọi là đường phân giác của ∆ABC.
2. Tính chất ba đường phân giác của tam giác
– Ba đường phân giác của một tam giác cùng đi qua một điểm
Nhận xét:
+ Để xác định giao điểm ba đường phân giác của một tam giác, ta chỉ cần vẽ hai đường phân giác bất kì và xác định giao điểm của hai đường đó.
+ Giao điểm ba đường phân giác của một tam giác cách đều ba cạnh của tam giác đó.
– Vậy, trong một tam giác ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.
Xem thêm
Lý thuyết Tính chất ba đường phân giác của tam giác – Toán 7 Cánh diều
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho có , các tia phân giác và cắt nhau tại I. Gọi D, E là chân các đường vuông góc hạ từ I đến các cạnh AB và AC. Khi đó ta có:
Câu 2:
Cho tam giác ABC có và . Tia phân giác của góc B cắt AC ở E. Tia phân giác của góc BAH cắt BE ở I. Khi đó tam giác AIE là tam giác gì?
Câu 3:
Cho có , các tia phân giác của và cắt nhau tại I. Gọi D, E là chân các đường vuông góc hạ từ I đến các cạnh MN và MP. Tính IE biết
Câu 4:
Cho , các tia phân giác của góc B và A cắt nhau tại O. Qua O kẻ đường thẳng song song với BC cắt AB tại M, cắt AC ở N. Cho ; . Tính MN?
Câu 5:
Cho tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I. Khi đó
Câu 7:
Cho có , các đường phân giác BE và CD của và cắt nhau tại I. Tính ?
Câu 8:
Cho cân tại A, trung tuyến AM. Gọi D là một nằm giữa A và M. Khi đó là tam giác gì?
Câu 9:
Cho có I cách đều ba cạnh của tam giác. Gọi N là giao điểm của hai tia phân giác góc ngoài tại B và C. Khi đó ta có:
Câu 10:
Cho cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có:
Câu 13:
Cho , các tia phân giác của góc B và A cắt nhau tại O. Qua O kẻ đường thẳng song song với BC cắt AB tại M, cắt AC ở N. Cho ; . Tính MN?
Câu 14:
Cho có , các đường phân giác BE và CD của và cắt nhau tại I. Tính ?
