Câu hỏi:
23/07/2024 783
Cho ∆ABC có AB < AC, lấy điểm E trên cạnh CA sao cho CE = BA. Các đường trung trực của các đoạn thẳng BE và CA cắt nhau tại I. Chọn khẳng định sai.
Cho ∆ABC có AB < AC, lấy điểm E trên cạnh CA sao cho CE = BA. Các đường trung trực của các đoạn thẳng BE và CA cắt nhau tại I. Chọn khẳng định sai.
A. ∆AIB = ∆EIC;
A. ∆AIB = ∆EIC;
B. AI là đường phân giác của ∆ABC;
C. ;
D. IA = IC.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
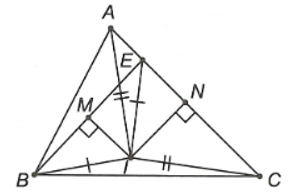
• Gọi M, N lần lượt là trung điểm BE, AC.
Vì IM là đường trung trực của đoạn thẳng BE nên IB = IE.
Vì IN là đường trung trực của đoạn thẳng AC nên IA = IC.
Do đó đáp án D đúng.
• Xét ∆AIB và ∆CIE, có:
IA = IC (chứng minh trên),
AB = CE (giả thiết),
IB = IE (chứng minh trên)
Do đó ∆AIB = ∆CIE (cạnh – cạnh – cạnh).
Vì vậy đáp án A sai do chưa đúng kí hiệu bằng nhau của hai tam giác.
• Ta có ∆AIB = ∆CIE (chứng minh trên).
Suy ra (cặp góc tương ứng).
Mà (do ∆IAC cân tại I).
Do đó .
Vì vậy đáp án C đúng.
• Ta có (chứng minh trên).
Suy ra AI là tia phân giác của .
Hay AI là đường phân giác của ∆ABC.
Do đó đáp án B đúng.
Vậy ta chọn đáp án C.
Đáp án đúng là: A
• Gọi M, N lần lượt là trung điểm BE, AC.
Vì IM là đường trung trực của đoạn thẳng BE nên IB = IE.
Vì IN là đường trung trực của đoạn thẳng AC nên IA = IC.
Do đó đáp án D đúng.
• Xét ∆AIB và ∆CIE, có:
IA = IC (chứng minh trên),
AB = CE (giả thiết),
IB = IE (chứng minh trên)
Do đó ∆AIB = ∆CIE (cạnh – cạnh – cạnh).
Vì vậy đáp án A sai do chưa đúng kí hiệu bằng nhau của hai tam giác.
• Ta có ∆AIB = ∆CIE (chứng minh trên).
Suy ra (cặp góc tương ứng).
Mà (do ∆IAC cân tại I).
Do đó .
Vì vậy đáp án C đúng.
• Ta có (chứng minh trên).
Suy ra AI là tia phân giác của .
Hay AI là đường phân giác của ∆ABC.
Do đó đáp án B đúng.
Vậy ta chọn đáp án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC nhọn, hai đường cao BM và CN. Trên tia đối của tia BM, lấy điểm P sao cho BP = AC. Trên tia đối của tia CN, lấy điểm Q sao cho CQ = AB. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC nhọn, hai đường cao BM và CN. Trên tia đối của tia BM, lấy điểm P sao cho BP = AC. Trên tia đối của tia CN, lấy điểm Q sao cho CQ = AB. Khẳng định nào sau đây đúng nhất?
Câu 2:
Cho ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA, lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khẳng định nào sau đây sai?
Cho ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA, lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khẳng định nào sau đây sai?
Câu 3:
Cho ∆ABC vuông cân tại A. Trên cạnh AB lấy điểm D bất kì (D ≠ A, B), trên tia đối của tia AC, lấy điểm E sao cho AD = AE. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC vuông cân tại A. Trên cạnh AB lấy điểm D bất kì (D ≠ A, B), trên tia đối của tia AC, lấy điểm E sao cho AD = AE. Khẳng định nào sau đây đúng nhất?
Câu 4:
Cho ∆ABC có , . Vẽ đường trung trực d của cạnh BC và d cắt BC tại M. Gọi E là điểm thuộc d (E nằm bên trong ∆ABC) sao cho . Khẳng định nào sau đây đúng nhất?
Cho ∆ABC có , . Vẽ đường trung trực d của cạnh BC và d cắt BC tại M. Gọi E là điểm thuộc d (E nằm bên trong ∆ABC) sao cho . Khẳng định nào sau đây đúng nhất?
Câu 5:
Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với mặt đất là 57°, khi đó độ nghiêng của chiếc thang đó so với bức tường là:
Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với mặt đất là 57°, khi đó độ nghiêng của chiếc thang đó so với bức tường là:
Câu 7:
Cho ∆ABC vuông tại A (AB < AC). Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC vuông tại A (AB < AC). Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC. Khẳng định nào sau đây đúng nhất?
Câu 8:
Cho ∆ABC cân tại A. Vẽ tia Ax // BC như hình bên.
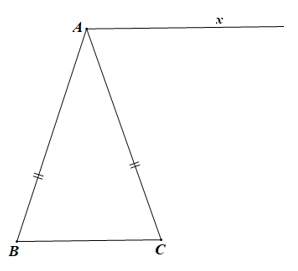
Lấy điểm O trên tia Ax, điểm M trên AB và điểm N trên AC sao cho . Hỏi ∆OMN là tam giác gì?
Cho ∆ABC cân tại A. Vẽ tia Ax // BC như hình bên.
Lấy điểm O trên tia Ax, điểm M trên AB và điểm N trên AC sao cho . Hỏi ∆OMN là tam giác gì?
Câu 9:
∆ABC có . Gọi O là trung điểm của BC. Vẽ BD ⊥ AO, CE ⊥ AO (D, E thuộc đường thẳng AO). So sánh AB và .
∆ABC có . Gọi O là trung điểm của BC. Vẽ BD ⊥ AO, CE ⊥ AO (D, E thuộc đường thẳng AO). So sánh AB và .
Câu 10:
Cho tam giác ABC (AC < BC), a là đường trung trực của đoạn thẳng AB. Lấy điểm M (M khác trung điểm của AB) nằm trên đường thẳng a.
So sánh độ dài của MA + MC với độ dài đoạn BC.
Cho tam giác ABC (AC < BC), a là đường trung trực của đoạn thẳng AB. Lấy điểm M (M khác trung điểm của AB) nằm trên đường thẳng a.
So sánh độ dài của MA + MC với độ dài đoạn BC.
Câu 11:
Cho các phát biểu:
(I) Ba đường trung tuyến của một tam giác đồng quy tại một điểm.
(II) Ba đường phân giác của một tam giác đồng quy tại một điểm.
(III) Ba đường trung trực của một tam giác đồng quy tại một điểm.
(IV) Ba đường cao của một tam giác đồng quy tại một điểm.
Số các phát biểu đúng là:
Cho các phát biểu:
(I) Ba đường trung tuyến của một tam giác đồng quy tại một điểm.
(II) Ba đường phân giác của một tam giác đồng quy tại một điểm.
(III) Ba đường trung trực của một tam giác đồng quy tại một điểm.
(IV) Ba đường cao của một tam giác đồng quy tại một điểm.
Số các phát biểu đúng là:
Câu 12:
Giao điểm của ba đường trung tuyến trong một tam giác được gọi là gì?
Câu 13:
Cho ∆ABC vuông tại A có . Kẻ AH ⊥ BC tại H và tia phân giác AD của (D ∈ BC). Trên cạnh AC lấy điểm E sao cho AE = AH. Trên tia đối của tia HA lấy điểm F sao cho HF = EC. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC vuông tại A có . Kẻ AH ⊥ BC tại H và tia phân giác AD của (D ∈ BC). Trên cạnh AC lấy điểm E sao cho AE = AH. Trên tia đối của tia HA lấy điểm F sao cho HF = EC. Khẳng định nào sau đây đúng nhất?
Câu 15:
Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:
Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:


