Cho tam giác ABC có BC = a, CA = b, AB = c, S là diện tích của tam giác ABC. Mệnh đề nào sau đây là sai?

Đáp án đúng là: C

*Phương pháp giải:

- Nắm vững công thức tính diện tích tam giác bằng lượng giác 

*Lời giải

Diện tích S của tam giác ABC là:

* Các lý thuyết cần nắm về hệ thức lượng trong tam giác và vectơ:

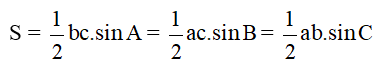
Định lí côsin

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:

a2 = b2 + c2 – 2bccosA,

b2 = c2 + a2 – 2cacosB,

 

c2 = a2 + b2 – 2abcosC.

Công thức tính diện tích tam giác:

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:

S = $\frac{1}{2}$bc.sinA = $\frac{1}{2}$ca.sinB = $\frac{1}{2}$ab.sinC

Công thức Heron:

Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, $p=\frac{a+b+c}{2}$. Khi đó, diện tích S của tam giác ABC là:$S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

Trong đó p là nửa chu vi tam giác ABC.

Tổng, hiệu và tích vô hướng của hai vectơ:

+ Quy tắc hình bình hành

 

Nếu ABCD là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.

+ Hai vectơ đối nhau:

 $\overrightarrow{a}+\left(-\overrightarrow{a}\right)=\left(-\overrightarrow{a}\right)+\overrightarrow{a}=\overrightarrow{0}$

 Hai vecto $\overrightarrow{a}$, $\overrightarrow{b}$ là hai vecto đối nhau khi và chỉ khi $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}$.

 

 Với hai điểm A, B, ta có: $\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow{0}$.

+ Hiệu 2 vectơ:

Với ba điểm bất kì A, B, O ta có: $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$.

+ Tích vectơ vô hướng

Với hai vecto bất kì $\overrightarrow{a}$, $\overrightarrow{b}$ và hai số thực h, k, ta có:

+) k($\overrightarrow{a}+\overrightarrow{b}$) = k$\overrightarrow{a}$ + k$\overrightarrow{b}$; k($\overrightarrow{a}-\overrightarrow{b}$) = k$\overrightarrow{a}$ - k$\overrightarrow{b}$;

+) (h + k)$\overrightarrow{a}$ = h$\overrightarrow{a}$ + k$\overrightarrow{a}$;

+) h(k$\overrightarrow{a}$) = (hk)$\overrightarrow{a}$;

+) 1$\overrightarrow{a}$ = $\overrightarrow{a}$; (-1)$\overrightarrow{a}$ = -$\overrightarrow{a}$.

+ Trung điểm của đoạn thẳng

 

Nếu I là trung điểm của đoạn thẳng AB thì $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$ với điểm M bất kì.

Xem thêm một số bài viết liên quan hay, chi tiết: 

Giải Toán 10 (Cánh diều) Bài tập cuối chương 4 trang 99, 100

Sách bài tập Toán 10 (Cánh diều) Bài ôn tập chương 4 

Trắc nghiệm Toán 10 Ôn tập chương 4 có đáp án