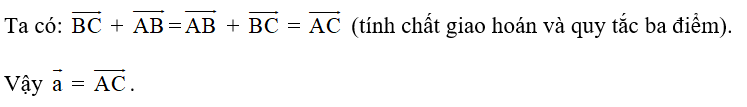Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2) (Nhận biết)
-
467 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Cho góc x thoả 0° < x < 90°. Mệnh đề nào sau đây là sai?
Xem đáp án
Đáp án đúng là: A
Vì 0° < x < 90° nên sin x > 0, cos x > 0, tan x > 0, cot x > 0.
Suy ra cos x < 0 sai.
Câu 2:
16/07/2024Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
Xem đáp án
Đáp án đúng là: D
Áp dụng mối liên hệ hai góc bù nhau, ta có:
sin α = sin β; cos α = – cos β; tan α = – tan β; cot α = – cot β.
Vậy đáp án A, B, C đúng và đáp án D sai.
Câu 3:
12/10/2024Cho tam giác ABC có BC = a, CA = b, AB = c, S là diện tích của tam giác ABC. Mệnh đề nào sau đây là sai?
Xem đáp án
Đáp án đúng là: C
*Phương pháp giải:
- Nắm vững công thức tính diện tích tam giác bằng lượng giác
*Lời giải
Diện tích S của tam giác ABC là:
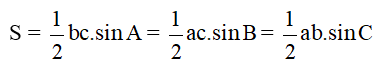
Định lí côsin
Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:
a2 = b2 + c2 – 2bccosA,
b2 = c2 + a2 – 2cacosB,
c2 = a2 + b2 – 2abcosC.
Công thức tính diện tích tam giác:
Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:
S = bc.sinA = ca.sinB = ab.sinC
Công thức Heron:
Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:
Cho tam giác ABC có BC = a, CA = b, AB = c, . Khi đó, diện tích S của tam giác ABC là:.
Trong đó p là nửa chu vi tam giác ABC.
Tổng, hiệu và tích vô hướng của hai vectơ:
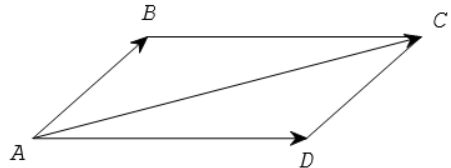
+ Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì .
+ Hai vectơ đối nhau:
Hai vecto , là hai vecto đối nhau khi và chỉ khi .
Với hai điểm A, B, ta có: .
+ Hiệu 2 vectơ:
Với ba điểm bất kì A, B, O ta có: .
+ Tích vectơ vô hướng
Với hai vecto bất kì , và hai số thực h, k, ta có:
+) k() = k + k; k() = k - k;
+) (h + k) = h + k;
+) h(k) = (hk);
+) 1 = ; (-1) = -.
+ Trung điểm của đoạn thẳng
Nếu I là trung điểm của đoạn thẳng AB thì với điểm M bất kì.
Câu 5:
19/07/2024Điền vào chỗ trống : “Vectơ không là vectơ có điểm đầu và điểm cuối … , kí hiệu là ”.
Xem đáp án
Đáp án đúng là: B
Vectơ không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là .
Câu 6:
23/07/2024Cho tam giác ABC vuông tại A, M là trung điểm BC. Khẳng định nào sau đây đúng?
Xem đáp án
Đáp án đúng là: C
Vì M là trung điểm của BC nên . Vậy đáp án C đúng.
Câu 7:
19/07/2024Điền vào chỗ trống: “ Tích vô hướng của hai vectơ và là một số thực, kí hiệu ., được xác định bởi công thức …”.
Xem đáp án
Đáp án đúng là: A
Tích vô hướng của hai vectơ và là một số thực, kí hiệu . , được xác định bởi công thức . = .