Câu hỏi:
12/10/2024 1,060
Cho tam giác ABC có a = 6, b = 5, c = 8. Tính cosA, S, r.
Cho tam giác ABC có a = 6, b = 5, c = 8. Tính cosA, S, r.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
* Phương pháp giải:
- Áp dụng công thức tính côsin và diện tích tam giác lượng giác, tính chu vi tam giác trong tam giác để tìm ra số đo góc, S và bán kính cần tìm
*Lời giải
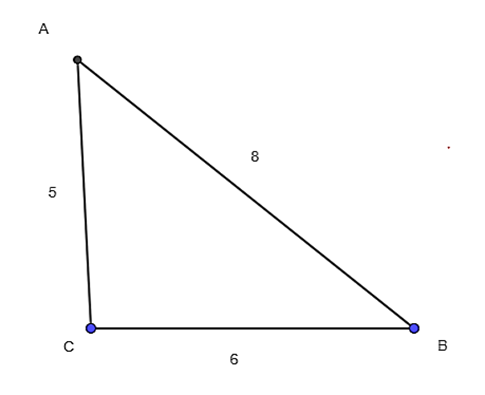
Xét ΔABC, có:
(định lí cos)
Diện tích tam giác ABC là:
(đvdt).
Nửa chu vi của tam giác ABC là:
Ta có: S = pr
Vậy cosA = 0,6625, S = 14,98 đvdt, r = 1,58.
* Các lý thuyết cần nắm về hệ thức lượng trong tam giác và vectơ:
Định lí côsin
Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:
a2 = b2 + c2 – 2bccosA,
b2 = c2 + a2 – 2cacosB,
c2 = a2 + b2 – 2abcosC.
Công thức tính diện tích tam giác:
Cho tam giác ABC có BC = a, CA = b và AB = c, gọi ha, hb, hc là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB; R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác;

Công thức Heron:
Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:
Cho tam giác ABC có BC = a, CA = b, AB = c, . Khi đó, diện tích S của tam giác ABC là:.
Trong đó p là nửa chu vi tam giác ABC.
Xem thêm một số bài viết liên quan hay, chi tiết:
Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án)
* Phương pháp giải:
- Áp dụng công thức tính côsin và diện tích tam giác lượng giác, tính chu vi tam giác trong tam giác để tìm ra số đo góc, S và bán kính cần tìm
*Lời giải

Xét ΔABC, có:
(định lí cos)
Diện tích tam giác ABC là:
(đvdt).
Nửa chu vi của tam giác ABC là:
Ta có: S = pr
Vậy cosA = 0,6625, S = 14,98 đvdt, r = 1,58.
Định lí côsin
Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:
a2 = b2 + c2 – 2bccosA,
b2 = c2 + a2 – 2cacosB,
c2 = a2 + b2 – 2abcosC.
Công thức tính diện tích tam giác:
Cho tam giác ABC có BC = a, CA = b và AB = c, gọi ha, hb, hc là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB; R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác;
Công thức Heron:
Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:
Cho tam giác ABC có BC = a, CA = b, AB = c, . Khi đó, diện tích S của tam giác ABC là:.
Trong đó p là nửa chu vi tam giác ABC.
Xem thêm một số bài viết liên quan hay, chi tiết:
Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC có b = 8, c = 5 và . Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài các cạnh còn lại của tam giác.
Cho tam giác ABC có b = 8, c = 5 và . Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài các cạnh còn lại của tam giác.
Câu 3:
Cho tam giác ABC, có AB = 5, AC = 8 và . Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.
Câu 4:
Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng Đông Nam rồi giữ nguyên vận tốc và đi tiếp.
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilômét (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng Định lí Pythagore (Pi – ta – go) để tính chính xác các số đo trong câu b hay không?
Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng Đông Nam rồi giữ nguyên vận tốc và đi tiếp.
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilômét (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng Định lí Pythagore (Pi – ta – go) để tính chính xác các số đo trong câu b hay không?
Câu 5:
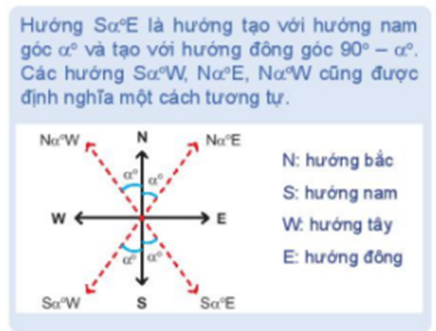
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S700E với vận tốc 70km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam theo vận tốc 8km/h. Sau 2 giờ kể từ khi bị hỏng, tàu neo đậu được vào một hòn đảo.
a) Tính khoảng cách từ cảng A tới nơi tàu neo đậu.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S700E với vận tốc 70km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam theo vận tốc 8km/h. Sau 2 giờ kể từ khi bị hỏng, tàu neo đậu được vào một hòn đảo.
a) Tính khoảng cách từ cảng A tới nơi tàu neo đậu.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.

Câu 7:
Từ định lý côsin hãy viết các công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC.
Từ định lý côsin hãy viết các công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC.
Câu 8:
Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như Hình 3.17. Dùng chế độ tính khoảng cách giữa hai điểm của Google Maps, một người xác định được các khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên Hòa Bình.
Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như Hình 3.17. Dùng chế độ tính khoảng cách giữa hai điểm của Google Maps, một người xác định được các khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên Hòa Bình.
Câu 9:
Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ.
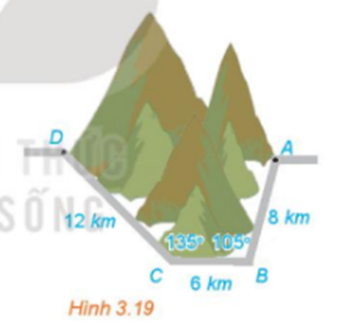
Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ.

Câu 12:
Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số đo góc A và kiểm tra tính đúng đắn của Định lí Côsin tại đỉnh A đối với tam giác đó.
Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số đo góc A và kiểm tra tính đúng đắn của Định lí Côsin tại đỉnh A đối với tam giác đó.
Câu 13:
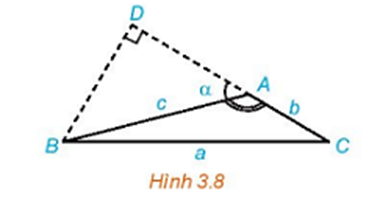
Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A.
a) Tính a2 theo BD2 và CD2.
b) Tính a2 theo b, c và DA.
c) Tính DA theo c và cosA.
d) Chứng minh a2 = b2 + c2 – 2bc.cosA.
Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A.
a) Tính a2 theo BD2 và CD2.
b) Tính a2 theo b, c và DA.
c) Tính DA theo c và cosA.
d) Chứng minh a2 = b2 + c2 – 2bc.cosA.

Câu 14:
Ngắm tháp rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí ta đứng tới Tháp Rùa. Em có biết vì sao?
Ngắm tháp rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí ta đứng tới Tháp Rùa. Em có biết vì sao?
Câu 15:
Từ bãi biển Vũng Chùa, Quảng Bình ta có thể ngắm được Đảo yến. Hãy đề xuất cách xác định bề rộng của hòn đảo (theo chiều ta ngắm được).

Từ bãi biển Vũng Chùa, Quảng Bình ta có thể ngắm được Đảo yến. Hãy đề xuất cách xác định bề rộng của hòn đảo (theo chiều ta ngắm được).