Câu hỏi:
10/07/2024 202
Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính →AB.→AO=?
Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính →AB.→AO=?
A. a;
B. 0;
C. a2;
D. 2a2.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D.
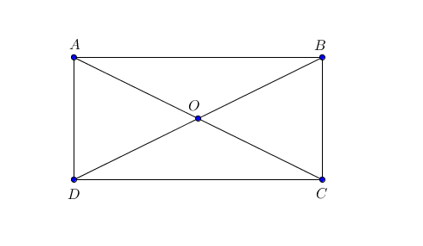
Do ABCD là hình chữ nhật nên ta có: BC = AD = a, AB = CD = 2a
Xét tam giác ABC vuông tại B
Áp dụng định lí Pythagore ta có:
AC2 = AB2 + BC2 = (2a)2 + a2 = 5a2
⇔ AC = a√5
⇒AO=12AC=12.a√5=a√52
Ta có:
(→AB, →AO)=^BAO=^BAC
Suy ra cos^BAO=cos^BAC=ABAC=2aa√5=2√5
|→AB|=AB=2a
|→AO|=AO=a√52
Ta có: →AB.→AO=|→AB|.|→AO|cos^BAO=2a.a√52.2√5=2a2.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính tích vô hướng →AH.→AC.
Cho tam giác ABC đều cạnh a, đường cao AH. Tính tích vô hướng →AH.→AC.
Câu 4:
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →AB.→DC.
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →AB.→DC.
Câu 7:
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính .
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính .
Câu 9:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính vô hướng giữa hai vectơ và bằng
Cho tam giác ABC đều cạnh a, đường cao AH. Tính vô hướng giữa hai vectơ và bằng


