Câu hỏi:
15/11/2024 10,054
Cho Elip (E) có phương trình chính tắc \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{25}} = 1.\)Tìm tọa độ các giao điểm của (E) với trục Ox, Oy và tọa độ các tiêu điểm của (E).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Ta có: \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{25}} = 1 \Leftrightarrow \frac{{{x^2}}}{{{7^2}}} + \frac{{{y^2}}}{{{5^2}}} = 1.\)
Do a > b > 0 nên elip (E) có a = 7, b = 5.
Ta có: c2 = a2 – b2 = 72 – 52 = 24, suy ra \(c = \sqrt {24} = 2\sqrt 6 \).
Vậy tọa độ các giao điểm của (E) với trục Ox là A1(– 7; 0), A2(7; 0), tọa độ các giao điểm của (E) với trục Oy là B1(0; – 5), B2(0; 5) và tọa độ các tiêu điểm của E là \({F_1}\left( { - 2\sqrt 6 ;\,\,0} \right),\,\,{F_2}\left( {2\sqrt 6 ;\,\,0} \right)\).
*Phương pháp giải:
+ Phương trình elip có dạng: 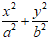
+ Ta xét phương trình: 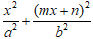
TH1: (*) có 2 nghiệm thì số giao điểm là 2 (đường thẳng cắt elip).
TH2: (*) có 1 nghiệm thì số giao điểm là 1 (đường thẳng tiếp xúc elip).
TH3: (*) vô nghiệm thì số giao điểm là 0 (đường thẳng và elip không có điểm chung).
*Lý thuyết:
1. Định nghĩa elip
Cho hai điểm cố định và và một độ dài không đổi 2a lớn hơn . Elip là tập hợp các điểm M trong mặt phẳng sao cho .
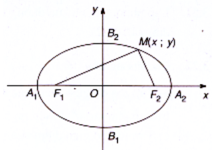
- Hình dạng của elip: Elip có hai trục đối xứng là Ox, Oy và có tâm đối xứng là gốc toạ độ.
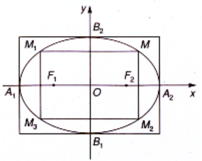
2. Các thành phần của Elip
Trong mặt phẳng Oxy
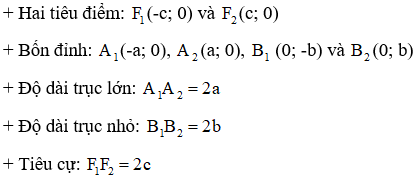
Xem thêm
Phương trình đường elip (Lý thuyết, công thức) các dạng bài tập và cách giải
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm tọa độ các tiêu điểm của đường hypebol trong mỗi trường hợp sau:
\(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\);
Câu 2:
B. Bài tập
Phương trình nào sau đây là phương trình chính tắc của elip?
Câu 3:
Những phương trình nào sau đây là phương trình chính tắc của hypebol?
a) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{9} = 1\);
b) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{9} = 1\);
c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{64}} = 1\);
d) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{9} = 1\).
Những phương trình nào sau đây là phương trình chính tắc của hypebol?
a) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{9} = 1\);
b) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{9} = 1\);
c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{64}} = 1\);
d) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{9} = 1\).
Câu 4:
Viết phương trình chính tắc của elip (E), biết tọa độ hai giao điểm của (E) với Ox và Oy lần lượt là A1(– 5; 0) và B2(0; \(\sqrt {10} \)).
Câu 6:
Những phương trình nào sau đây là phương trình chính tắc của parabol?
y2 = – 2x;
Những phương trình nào sau đây là phương trình chính tắc của parabol?
y2 = – 2x;
Câu 7:
Viết phương trình chính tắc của hypebol (H), biết \(N\left( {\sqrt {10} ;\,\,2} \right)\) nằm trên (H) và hoành độ một giao điểm của (H) đối với trục Ox bằng 3.
Câu 8:
Viết phương trình hypebol sau đây dưới dạng chính tắc: 4x2 – 9y2 = 1.
Câu 9:
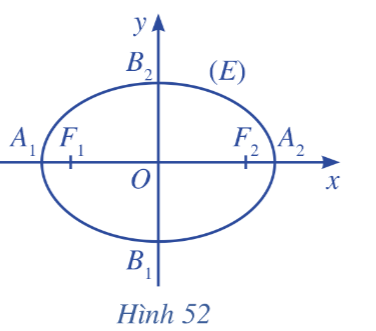
Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho MF1 + MF2 = 2a, ở đó F1F2 = 2c (với a > c > 0).
Ta chọn hệ trục tọa độ Oxy có gốc là trung điểm của F1F2, trục Oy là đường trung trực của F1F2 và F2 nằm trên tia Ox (Hình 52). Khi đó, F1(– c; 0) và F2(c; 0) là hai tiêu điểm của elip (E). Chứng minh rằng:
a) A1(– a; 0) và A2(a; 0) đều là giao điểm của elip (E) với trục Ox.
Câu 10:
Lập phương trình chính tắc của elip (E) đi qua hai điểm M(0; 3) và \(N\left( {3;\, - \frac{{12}}{5}} \right)\).
Câu 11:
Viết phương trình chính tắc của đường parabol, biết tiêu điểm là F(6; 0).
Câu 12:
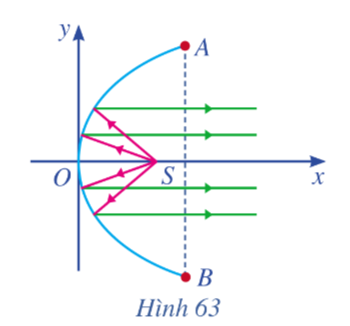
Một chiếc đèn có mặt cắt ngang là hình parabol (Hình 63). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.

Câu 13:
Để lập phương trình của đường hypebol trong mặt phẳng, trước tiên ta sẽ chọn hệ trục tọa độ Oxy thuận tiện nhất.
Tương tự elip, ta chọn trục Ox là đường thẳng F1F2, trục Oy là đường trung trực của đoạn thẳng F1F2 = 2c (c > 0), gốc tọa độ O là trung điểm của đoạn thẳng F1F2 (Hình 54).
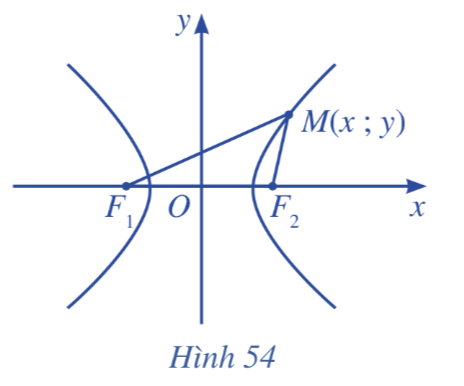
Tìm tọa độ của hai tiêu điểm F1, F2.
Để lập phương trình của đường hypebol trong mặt phẳng, trước tiên ta sẽ chọn hệ trục tọa độ Oxy thuận tiện nhất.
Tương tự elip, ta chọn trục Ox là đường thẳng F1F2, trục Oy là đường trung trực của đoạn thẳng F1F2 = 2c (c > 0), gốc tọa độ O là trung điểm của đoạn thẳng F1F2 (Hình 54).

Tìm tọa độ của hai tiêu điểm F1, F2.
Câu 14:
Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có A1A2 = 768 800 km và B1B2 = 767 619 km (Nguồn: Ron Larson (2014), Precalculus Real Mathematics, Real People, Cengage) (Hình 62). Viết phương trình chính tắc của elip đó.
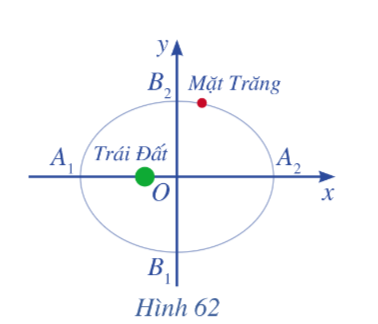
Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có A1A2 = 768 800 km và B1B2 = 767 619 km (Nguồn: Ron Larson (2014), Precalculus Real Mathematics, Real People, Cengage) (Hình 62). Viết phương trình chính tắc của elip đó.

Câu 15:
Lấy đường thẳng ∆ và một điểm F không thuộc ∆. Lấy một ê ke ABC (vuông ở A) và một đoạn dây không đàn hồi, có độ dài bằng AB. Đính một đầu dây vào điểm F, đầu kia vào đỉnh B của ê ke. Đặt ê ke sao cho cạnh AC nằm trên ∆, lấy đầu bút chì (kí hiệu là điểm M) ép sát sợi dây vào cạnh AB và giữ căng sợi dây. Lúc này, sợi dây chính là đường gấp khúc BMF.
Cho cạnh AC của ê ke trượt trên ∆ (Hình 55). Khi đó, đầu bút chì M sẽ vạch nên một đường mà ta gọi là đường parabol.
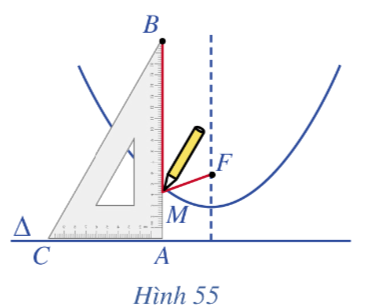
Khi M thay đổi, có nhận xét gì về khoảng cách từ M đến F và khoảng cách từ M đến đường thẳng ∆?
Lấy đường thẳng ∆ và một điểm F không thuộc ∆. Lấy một ê ke ABC (vuông ở A) và một đoạn dây không đàn hồi, có độ dài bằng AB. Đính một đầu dây vào điểm F, đầu kia vào đỉnh B của ê ke. Đặt ê ke sao cho cạnh AC nằm trên ∆, lấy đầu bút chì (kí hiệu là điểm M) ép sát sợi dây vào cạnh AB và giữ căng sợi dây. Lúc này, sợi dây chính là đường gấp khúc BMF.
Cho cạnh AC của ê ke trượt trên ∆ (Hình 55). Khi đó, đầu bút chì M sẽ vạch nên một đường mà ta gọi là đường parabol.

Khi M thay đổi, có nhận xét gì về khoảng cách từ M đến F và khoảng cách từ M đến đường thẳng ∆?


