3.    Cho a, b, c là độ dài ba cạnh của một tam giác.

Mệnh đề nào sau đây không đúng?

Đáp án đúng là D

Lời giải

Do a, b, c là độ dài ba cạnh của một tam giác nên theo bất đẳng thức tam giác ta có:

* $a<b+c\iff a^2<a\left(b+c\right)\iff a^2<ab+ac$

* $a+c>b\iff b\left(a+c\right)>b^2\iff ab+bc>b^2$

* $$\begin{gathered} \left|b-c\right|<a\iff {\left(b-c\right)}^2<a^2\iff b^2-2bc+c^2<a^2 \\ \iff b^2+c^2<a^2+2bc \end{gathered}$$

Do đó, mệnh đề D không đúng.

*Phương pháp giải:

Biến đổi các mệnh đề và áp dụng bất đẳng thức tam giác.

$a,b,c$ là độ dài ba cạnh của một tam giác thì $a>0,b>0,c>0$.

Bất đẳng thức tam giác: $\{\begin{array}{l}a+b>c\\ a+c>b\\ b+c>a\end{array}$

*Lý thuyết:

1.1. Góc đối diện với cạnh lớn hơn

– Trong tam giác ABC:

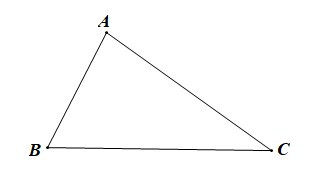
• Góc A được gọi là góc đối diện với cạnh BC;

• Góc B được gọi là góc đối diện với cạnh CA;

• Góc C được gọi là góc đối diện với cạnh AB.

– Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Trong tam giác ABC, nếu AC > AB thì $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}.$

1.2. Cạnh đối diện với góc lớn hơn

– Trong tam giác ABC:

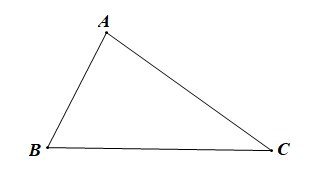
• Cạnh BC được gọi là cạnh đối diện với góc A;

• Cạnh CA được gọi là cạnh đối diện với góc B;

• Cạnh AB được gọi là cạnh đối diện với góc C.

– Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Trong tam giác ABC, nếu $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}$ thì AC > AB.

– Nhận xét:

+ Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.

+ Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

2. Bất đẳng thức tam giác

– Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Trong tam giác ABC, ta có: AB + BC > AC; AB + AC > BC; AC + BC > AB.

Các bất đảng thức này gọi là các bất đẳng thức tam giác.

– Nhận xét: Trong một tam giác, hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại.

Xem thêm

Lý thuyết Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác – Toán 7 Cánh diều 

Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác có đáp án - Toán lớp 7