Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
b)
Đồ thị hàm số y = 2x – 5 là đường thẳng đi qua điểm (0; –5), (2,5; 0)
Đồ thị hàm số y = x2 – 4x – 1 là parabol có bề lõm hướng lên, đỉnh là điểm (2; –5), trục đối xứng x = 2, đi qua điểm (0; –1).
Đồ thị hai hàm số như hình vẽ:
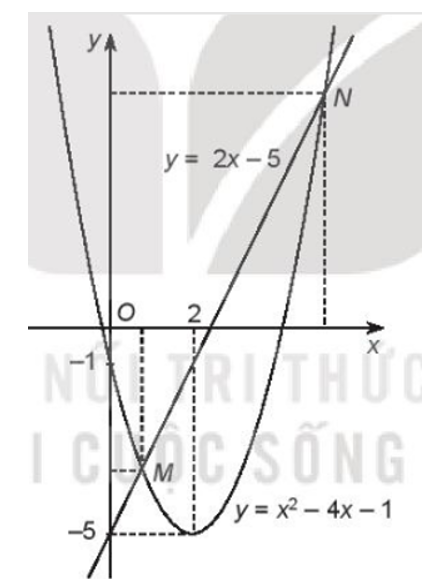
Hai đồ thị hàm số có giao điểm là M và N
Xét phương trình hoành độ giao điểm của hai đồ thị:
x2 – 4x – 1 = 2x – 5
⇔ x2 – 6x + 4 = 0
⇔ hoặc
Với ta được. Vậy .
Với ta được. Vậy .
b)
Đồ thị hàm số y = 2x – 5 là đường thẳng đi qua điểm (0; –5), (2,5; 0)
Đồ thị hàm số y = x2 – 4x – 1 là parabol có bề lõm hướng lên, đỉnh là điểm (2; –5), trục đối xứng x = 2, đi qua điểm (0; –1).
Đồ thị hai hàm số như hình vẽ:
Hai đồ thị hàm số có giao điểm là M và N
Xét phương trình hoành độ giao điểm của hai đồ thị:
x2 – 4x – 1 = 2x – 5
⇔ x2 – 6x + 4 = 0
⇔ hoặc
Với ta được. Vậy .
Với ta được. Vậy .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Điều kiện cần và đủ của tham số m để parabol (P): y = x2 – 2x + m – 1 cắt trục Ox tại hai điểm phân biệt nằm về hai phía của trục tung là
Điều kiện cần và đủ của tham số m để parabol (P): y = x2 – 2x + m – 1 cắt trục Ox tại hai điểm phân biệt nằm về hai phía của trục tung là
Câu 5:
Phương trình (m + 2) x2 – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi
Phương trình (m + 2) x2 – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi
Câu 9:
Các giá trị của tham số m làm cho biểu thức f(x) = x2 + 4x + m – 5 luôn dương là
Các giá trị của tham số m làm cho biểu thức f(x) = x2 + 4x + m – 5 luôn dương là
Câu 10:
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 12x + 36 ?
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 12x + 36 ?
Câu 12:
c) Từ đồ thị vẽ ở ý b) hãy chỉ ra các khoảng đồng biến, khoảng nghịch biến của hàm số.
c) Từ đồ thị vẽ ở ý b) hãy chỉ ra các khoảng đồng biến, khoảng nghịch biến của hàm số.
Câu 13:
b) Tam thức bậc hai y = –x2 + mx – 1 có dấu không phụ thuộc vào x;
b) Tam thức bậc hai y = –x2 + mx – 1 có dấu không phụ thuộc vào x;
Câu 14:
Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập xác định, tập giá trị, khoảng đồng biến và khoảng nghịch biến của chúng.
a) y = |x – 1| + |x + 1|;
Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập xác định, tập giá trị, khoảng đồng biến và khoảng nghịch biến của chúng.
a) y = |x – 1| + |x + 1|;
Câu 15:
c) Giả sử vận tốc ban đầu v0 không đổi. Từ kết quả câu b) hãy xác định góc ném α để độ cao lớn nhất của vật đạt giá trị lớn nhất.
c) Giả sử vận tốc ban đầu v0 không đổi. Từ kết quả câu b) hãy xác định góc ném α để độ cao lớn nhất của vật đạt giá trị lớn nhất.


