Sách bài tập Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Giải SBT Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Bài 1 trang 50 sách bài tập Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức:

a) $\frac{5\sqrt{2}}{\sqrt{15}};$

b) $-\frac{2\sqrt{5}}{\sqrt{18}};$

c) $\frac{6a}{\sqrt{2a{b}^2}}$ (a > 0, b > 0).

Lời giải:

a) $\frac{5\sqrt{2}}{\sqrt{15}}=\frac{5\sqrt{2}\cdot \sqrt{15}}{{\left(\sqrt{15}\right)}^2}=\frac{5\sqrt{2\cdot 15}}{15}$$=\frac{5\sqrt{30}}{15}=\frac{\sqrt{30}}{3}.$

b) $-\frac{2\sqrt{5}}{\sqrt{18}}=-\frac{2\sqrt{5}\cdot \sqrt{18}}{{\left(\sqrt{18}\right)}^2}=-\frac{2\sqrt{5}\cdot \sqrt{3^2\cdot 2}}{18}=$$-\frac{2\sqrt{5}\cdot 3\sqrt{2}}{18}=\frac{6\sqrt{5\cdot 2}}{18}=\frac{\sqrt{10}}{3}$

c) Với a > 0, b > 0, ta có:

$\frac{6a}{\sqrt{2a{b}^2}}=\frac{6a}{\sqrt{2a}\cdot \sqrt{b^2}}=\frac{6a}{\sqrt{2a}\cdot b}$$=\frac{6a\cdot \sqrt{2a}}{b\cdot {\left(\sqrt{2a}\right)}^2}=\frac{6a\sqrt{2a}}{b\cdot 2a}=\frac{3\sqrt{2a}}{b}.$

Bài 2 trang 50 sách bài tập Toán 9 Tập 1: Khử mẫu của biểu thức lấy căn:

a) $\sqrt{\frac{10}{11}};$

b) $\sqrt{\frac{42}{300}};$

c) $\sqrt{\frac{5a}{12b}}.$ (a ≥ 0; b > 0)

Lời giải:

a) $\sqrt{\frac{10}{11}}=\sqrt{\frac{10\cdot 11}{{11}^2}}=\frac{\sqrt{110}}{\sqrt{{11}^2}}=\frac{\sqrt{110}}{11}.$

b) $\sqrt{\frac{42}{300}}=\sqrt{\frac{14\cdot 3}{3\cdot 100}}=\sqrt{\frac{14}{100}}$$=\frac{\sqrt{14}}{\sqrt{100}}=\frac{\sqrt{14}}{\sqrt{{10}^2}}=\frac{\sqrt{14}}{10}.$

c) $\sqrt{\frac{5a}{12b}}=\sqrt{\frac{5a}{4\cdot 3b}}=\sqrt{\frac{5a}{2^2\cdot 3b}}=$$\sqrt{\frac{5a\cdot 3b}{2^2\cdot 3^2\cdot b^2}}=\frac{\sqrt{15ab}}{\sqrt{{\left(2\cdot 3\right)}^2\cdot b^2}}=\frac{\sqrt{15ab}}{6b}.$

Bài 3 trang 50 sách bài tập Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:

a) $\frac{\sqrt{6}+2}{\sqrt{6}-2};$

b) $\frac{1}{\sqrt{2}\left(\sqrt{5}-1\right)};$

c) $\frac{x-1}{2\sqrt{x}-\sqrt{x+3}}$ (x ≥ 0, x ≠ 1).

Lời giải:

a) $\frac{\sqrt{6}+2}{\sqrt{6}-2}=\frac{{\left(\sqrt{6}+2\right)}^2}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}$

$=\frac{{\left(\sqrt{6}\right)}^2+2\sqrt{6}\cdot 2+4}{{\left(\sqrt{6}\right)}^2-2^2}=\frac{6+4\sqrt{6}+4}{6-4}$

$=\frac{10+4\sqrt{6}}{2}=\frac{2\left(5+2\sqrt{6}\right)}{2}=5+2\sqrt{6}.$

b) $\frac{1}{\sqrt{2}\left(\sqrt{5}-1\right)}=\frac{\sqrt{2}\cdot \left(\sqrt{5}+1\right)}{{\left(\sqrt{2}\right)}^2\cdot \left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}$

$=\frac{\sqrt{10}+\sqrt{2}}{2\cdot \left[{\left(\sqrt{5}\right)}^2-1^2\right]}=\frac{\sqrt{10}+\sqrt{2}}{2\cdot \left(5-1\right)}$$=\frac{\sqrt{10}+\sqrt{2}}{8}.$

c) Với x ≥ 0, x ≠ 1, ta có:

$\frac{x-1}{2\sqrt{x}-\sqrt{x+3}}=\frac{\left(x-1\right)\left(2\sqrt{x}+\sqrt{x+3}\right)}{\left(2\sqrt{x}-\sqrt{x+3}\right)\left(2\sqrt{x}+\sqrt{x+3}\right)}$

$=\frac{\left(x-1\right)\left(2\sqrt{x}+\sqrt{x+3}\right)}{{\left(2\sqrt{x}\right)}^2-{\left(\sqrt{x+3}\right)}^2}$

$=\frac{\left(x-1\right)\left(2\sqrt{x}+\sqrt{x+3}\right)}{4x-\left(x+3\right)}$

$=\frac{\left(x-1\right)\left(2\sqrt{x}+\sqrt{x+3}\right)}{3x-3}$

$=\frac{\left(x-1\right)\left(2\sqrt{x}+\sqrt{x+3}\right)}{3\left(x-1\right)}$

$=\frac{2\sqrt{x}+\sqrt{x+3}}{3}.$

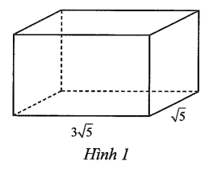
Bài 4 trang 51 sách bài tập Toán 9 Tập 1: Cho hình hộp chữ nhật với chiều dài $3\sqrt{5}$ cm, chiều rộng $\sqrt{5}$ cm và thể tích $30\sqrt{5}$ cm³ như Hình 1. Tính tổng độ dài các cạnh của hình hộp chữ nhật đó

Lời giải:

Gọi chiều cao hình hộp chữ nhật là h (cm) (h > 0).

Khi đó, thể tích của hình hộp chữ nhật đó là:

$3\sqrt{5}\cdot \sqrt{5}\cdot h=3\cdot 5\cdot h=15h$(cm³).

Theo bài, thể tích của hình hộp chữ nhật bằng $30\sqrt{5}$cm nên ta có:

$15h=30\sqrt{5},$suy ra: $h=\frac{30\sqrt{5}}{15}=2\sqrt{5}$(cm).

Tổng độ dài các cạnh của hình hộp chữ nhật là:

$4\cdot \left(3\sqrt{5}+\sqrt{5}+2\sqrt{5}\right)=4\cdot 6\sqrt{5}=24\sqrt{5}$ (cm).

Bài 5 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

a) $\sqrt{8}\cdot \sqrt{18}:\frac{\sqrt{5}}{\sqrt{2}};$

b) $\sqrt{75}:\sqrt{45}\cdot \frac{3}{\sqrt{10}}.$

Lời giải:

a) $\sqrt{8}\cdot \sqrt{18}:\frac{\sqrt{5}}{\sqrt{2}}=\sqrt{8\cdot 18}\cdot \frac{\sqrt{2}}{\sqrt{5}}$

$=\sqrt{144}\cdot \frac{\sqrt{2}\cdot \sqrt{5}}{{\left(\sqrt{5}\right)}^2}=12\cdot \frac{\sqrt{2\cdot 5}}{5}=\frac{12\sqrt{10}}{5}.$

b) $\sqrt{75}:\sqrt{45}\cdot \frac{3}{\sqrt{10}}=\frac{\sqrt{75}}{\sqrt{45}}\cdot \frac{3}{\sqrt{2\cdot 5}}$

$=\sqrt{\frac{75}{45}}\cdot \frac{3}{\sqrt{2}\cdot \sqrt{5}}=\sqrt{\frac{5}{3}}\cdot \frac{3}{\sqrt{2}\cdot \sqrt{5}}$

$=\frac{\sqrt{5}}{\sqrt{3}}\cdot \frac{{\left(\sqrt{3}\right)}^2}{\sqrt{2}\cdot \sqrt{5}}=\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{3}\cdot \sqrt{2}}{{\left(\sqrt{2}\right)}^2}=\frac{\sqrt{6}}{2}.$

Bài 6 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

a) $4\sqrt{24}+\sqrt{6}-2\sqrt{54};$

b) $2\sqrt{45}-\sqrt{125}-\frac{15}{\sqrt{5}};$

c) $\sqrt{8}-\sqrt{27}-\sqrt{32}+\sqrt{75};$

d) $\left(2-\sqrt{10}\right)\left(\sqrt{2}-\sqrt{5}\right).$

Lời giải:

a) $4\sqrt{24}+\sqrt{6}-2\sqrt{54}$

$=4\cdot \sqrt{2^2\cdot 6}+\sqrt{6}-2\cdot \sqrt{3^2\cdot 6}$

$=4\cdot 2\sqrt{6}+\sqrt{6}-2\cdot 3\sqrt{6}$

$=8\sqrt{6}+\sqrt{6}-6\sqrt{6}$

$=3\sqrt{6}.$

b) $2\sqrt{45}-\sqrt{125}-\frac{15}{\sqrt{5}}$

$=2\cdot \sqrt{3^2\cdot 5}-\sqrt{5^2\cdot 5}-\frac{15\cdot \sqrt{5}}{{\left(\sqrt{5}\right)}^2}$

$=2\cdot 3\sqrt{5}-5\sqrt{5}-\frac{15\cdot \sqrt{5}}{5}$

$=6\sqrt{5}-5\sqrt{5}-3\sqrt{5}=-2\sqrt{5}.$

c) $\sqrt{8}-\sqrt{27}-\sqrt{32}+\sqrt{75}$

$=\sqrt{2^2\cdot 2}-\sqrt{3^2\cdot 3}-\sqrt{4^2\cdot 2}+\sqrt{5^2\cdot 3}$

$=2\sqrt{2}-3\sqrt{3}-4\sqrt{2}+5\sqrt{3}$

$=-2\sqrt{2}+2\sqrt{3}.$

d) $\left(2-\sqrt{10}\right)\left(\sqrt{2}-\sqrt{5}\right)$

$=2\sqrt{2}-2\sqrt{5}-\sqrt{10}\cdot \sqrt{2}+\sqrt{10}\cdot \sqrt{5}$

$=2\sqrt{2}-2\sqrt{5}-\sqrt{10\cdot 2}+\sqrt{10\cdot 5}$

$=2\sqrt{2}-2\sqrt{5}-\sqrt{20}+\sqrt{50}$

$=2\sqrt{2}-2\sqrt{5}-\sqrt{2^2\cdot 5}+\sqrt{5^2\cdot 2}$

$=2\sqrt{2}-2\sqrt{5}-2\sqrt{5}+5\sqrt{2}$

$=7\sqrt{2}-4\sqrt{5}.$

Bài 7 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức (biết a > 0, b > 0):

a) $\sqrt{4a}+\sqrt{25a}-6\sqrt{\frac{a}{4}};$

b) $b\sqrt{\frac{a}{b}}+a\sqrt{\frac{b}{a}}.$

Lời giải:

Với a > 0, b > 0, ta có:

a) $\sqrt{4a}+\sqrt{25a}-6\sqrt{\frac{a}{4}}$

$=\sqrt{2^2\cdot a}+\sqrt{5^2\cdot a}-6\cdot \sqrt{\frac{a}{2^2}}$

$=2\sqrt{a}+5\sqrt{a}-6\cdot \frac{\sqrt{a}}{2}$

$=2\sqrt{a}+5\sqrt{a}-3\sqrt{a}$

$=4\sqrt{a}.$

b) $b\sqrt{\frac{a}{b}}+a\sqrt{\frac{b}{a}}$

$=\sqrt{b^2\cdot \frac{a}{b}}+\sqrt{a^2\cdot \frac{b}{a}}$

$=\sqrt{ab}+\sqrt{ab}=2\sqrt{ab}.$

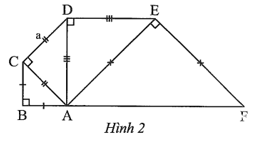
Bài 8 trang 51 sách bài tập Toán 9 Tập 1: Một phần khung của một cây cầu gồm các thanh thép tạo thành các tam giác vuông cân như Hình 2. Biết rằng cạnh CD có độ dài a (m). Tính độ dài của đoạn BF theo a.

Lời giải:

Do ∆ABC cân tại B nên BA = BC.

Do ∆ACD cân tại C nên CA = CD.

Do ∆ADE cân tại D nên DA = DE.

Do ∆AEF cân tại E nên EA = EF.

Xét ∆ACD vuông tại C, theo định lí Pythagore, ta có:

$DA=\sqrt{C{A}^2+C{D}^2}=\sqrt{2C{D}^2}=CD\sqrt{2}=a\sqrt{2}$(m).

Xét ∆ADE vuông tại D, theo định lí Pythagore, ta có:

$EA=\sqrt{D{A}^2{\text{+DE}}^2}=\sqrt{2D{A}^2}=DA\sqrt{2}=a\sqrt{2}\cdot \sqrt{2}=2a$ (m).

Xét ∆AEF vuông tại E, theo định lí Pythagore, ta có:

$AF=\sqrt{E{A}^2{\text{+EF}}^2}=\sqrt{2E{A}^2}=EA\sqrt{2}=2a\cdot \sqrt{2}=2a\sqrt{2}$(m).

Xét ∆ABC vuông tại B, theo định lí Pythagore, ta có:

$CA=\sqrt{B{A}^2+B{C}^2}=\sqrt{2B{A}^2}=BA\sqrt{2}$

Suy ra $BA=\frac{CA}{\sqrt{2}}=\frac{CD}{\sqrt{2}}=\frac{a}{\sqrt{2}}=\frac{a\sqrt{2}}{2}$(m).

Từ đó, $BF=BA+AF=\frac{a\sqrt{2}}{2}+2a\sqrt{2}=\frac{a\sqrt{2}}{2}+\frac{4a\sqrt{2}}{2}=\frac{5a\sqrt{2}}{2}$

Vậy $BF=\frac{5a\sqrt{2}}{2}\text{ (m).}$

Bài 9 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức (biết x > 0; y > 0):

a) $2\left(\sqrt{x}+\sqrt{y}\right)-\frac{x-y}{\sqrt{x}+\sqrt{y}};$

b) $\frac{x\sqrt{x}+y\sqrt{y}}{x-\sqrt{xy}+y}.$

Lời giải:

a) $2\left(\sqrt{x}+\sqrt{y}\right)-\frac{x-y}{\sqrt{x}+\sqrt{y}}$

$=2\left(\sqrt{x}+\sqrt{y}\right)-\frac{{\left(\sqrt{x}\right)}^2-{\left(\sqrt{y}\right)}^2}{\sqrt{x}+\sqrt{y}}$

$=2\left(\sqrt{x}+\sqrt{y}\right)-\frac{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}$

$=2\sqrt{x}+2\sqrt{y}-\left(\sqrt{x}-\sqrt{y}\right)$

$=2\sqrt{x}+2\sqrt{y}-\sqrt{x}+\sqrt{y}$

$=\sqrt{x}+3\sqrt{y}.$

b) $\frac{x\sqrt{x}+y\sqrt{y}}{x-\sqrt{xy}+y}$

$=\frac{{\left(\sqrt{x}\right)}^3+{\left(\sqrt{y}\right)}^3}{x-\sqrt{xy}+y}$

$=\frac{\left(\sqrt{x}+\sqrt{y}\right)\left[{\left(\sqrt{x}\right)}^2-\sqrt{x}\cdot \sqrt{y}+{\left(\sqrt{y}\right)}^2\right]}{x-\sqrt{xy}+y}$

$=\frac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{x-\sqrt{xy}+y}$

$=\sqrt{x}+\sqrt{y}.$

Bài 10 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn và tính giá trị của biểu thức $A=\frac{x-16}{x+\sqrt{x}+1}:\frac{\sqrt{x}+4}{x\sqrt{x}-1}$ tại x = 0,64.

Lời giải:

$A=\frac{x-16}{x+\sqrt{x}+1}:\frac{\sqrt{x}+4}{x\sqrt{x}-1}$

$=\frac{{\left(\sqrt{x}\right)}^2-4^2}{x+\sqrt{x}+1}\cdot \frac{{\left(\sqrt{x}\right)}^3-1}{\sqrt{x}+4}$

$=\frac{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}{x+\sqrt{x}+1}\cdot \frac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}+4}$

$=\left(\sqrt{x}-4\right)\left(\sqrt{x}-1\right).$

Thay x = 0,64 vào biểu thức trên ta được:

$A=\left(\sqrt{\mathrm{0,64}}-4\right)\left(\sqrt{\mathrm{0,64}}-1\right)$

$=\left(\sqrt{{\mathrm{0,8}}^2}-4\right)\left(\sqrt{{\mathrm{0,8}}^2}-1\right)$

= (0,8 ‒ 4)(0,8 ‒ 1)

= ‒3,2.(‒0,2) = 0,64.

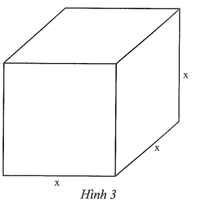
Bài 11 trang 51 sách bài tập Toán 9 Tập 1: Một chiếc thùng hình lập phương có chiều dài cạnh là x (cm).

a) Viết công thức tính thể tích V (cm³) và tổng diện tích S (cm²) các mặt của hình lập phương theo x.

b) Viết công thức tính x theo S.

c) Viết công thức tính V theo S. Tính V khi S = 50 cm².

Lời giải:

a) Thể tích của hình lập phương là: V = x³ (cm³).

Diện tích 1 mặt của hình lập phương là: x² (cm²).

Do hình lập phương có 6 mặt đều là hình vuông cạnh x (cm) nên diện tích các mặt của hình lập phương là:

S = 6x² (cm²).

b) Từ S = 6x², ta có: $x^2=\frac{S}{6},$ suy ra $x=\sqrt{\frac{S}{6}}$ (cm) (do x > 0).

Vậy công thức tính x theo S là: $x=\sqrt{\frac{S}{6}}$(cm).

c) Thay $x=\sqrt{\frac{S}{6}}$ vào biểu thức V = x³ ta được:

$V={\left(\sqrt{\frac{S}{6}}\right)}^3=\frac{{\left(\sqrt{S}\right)}^3}{{\left(\sqrt{6}\right)}^3}=\frac{{\left(\sqrt{S}\right)}^2\cdot \sqrt{S}}{{\left(\sqrt{6}\right)}^2\cdot \sqrt{6}}=\frac{S\sqrt{S}}{6\sqrt{6}}=\frac{S\sqrt{6S}}{36}$(cm³).

Thay S = 50 vào biểu thức trên ta được:

$V=\frac{50\sqrt{6\cdot 50}}{36}=\frac{50\cdot \sqrt{{10}^2\cdot 3}}{36}=\frac{50\cdot 10\cdot \sqrt{3}}{36}=\frac{125\sqrt{3}}{9}$(cm³).

Vậy $V=\frac{125\sqrt{3}}{9}{\text{ (cm}}^3\text{).}$

Lý thuyết Biến đổi đơn giản biểu thức chứa căn thức bậc hai

1. Trục căn thức ở mẫu

- Với các biểu thức A và B thỏa mãn $AB\ge 0,B\ne 0$, ta có: $\sqrt{\frac{A}{B}}=\sqrt{\frac{AB}{B^2}}=\frac{\sqrt{AB}}{\sqrt{B^2}}=\frac{\sqrt{AB}}{\left|B\right|}$. - Với các biểu thức A, B và B > 0, ta có $\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}$. - Với các biểu thức A, B, C mà $A\ge 0,A\ne B^2$, ta có: $\frac{C}{\sqrt{A}+B}=\frac{C\left(\sqrt{A}-B\right)}{A-B^2};\frac{C}{\sqrt{A}-B}=\frac{C\left(\sqrt{A}+B\right)}{A-B^2}$. - Với các biểu thức A, B, C mà $A\ge 0,B\ge 0,A\ne B$, ta có: $\frac{C}{\sqrt{A}+\sqrt{B}}=\frac{C\left(\sqrt{A}-\sqrt{B}\right)}{A-B};\frac{C}{\sqrt{A}-\sqrt{B}}=\frac{C\left(\sqrt{A}+\sqrt{B}\right)}{A-B}$.

Ví dụ:

$\frac{2}{3\sqrt{5}}=\frac{2\sqrt{5}}{3{\left(\sqrt{5}\right)}^2}=\frac{2\sqrt{5}}{3.5}=\frac{2\sqrt{5}}{15}$;

$\frac{a}{3-2\sqrt{2}}=\frac{a\left(3+2\sqrt{2}\right)}{\left(3-2\sqrt{2}\right).\left(3+2\sqrt{2}\right)}=\frac{a\left(3+2\sqrt{2}\right)}{3^2-{\left(2\sqrt{2}\right)}^2}=\frac{a\left(3+2\sqrt{2}\right)}{9-8}=\left(3+2\sqrt{2}\right)a$.

2. Rút gọn biểu thức chứa căn thức bậc hai

Để rút gọn biểu thức có chứa căn thức bậc hai, ta cần vận dụng thích hợp các tính chất (giao hoán, kết hợp, phân phối) của các phép tính, quy tắc về thứ tự thực hiện và phép biến đổi đã biết.

Ví dụ:

$\begin{array}{l}A=2\sqrt{3}-\sqrt{75}+\sqrt{{\left(1-\sqrt{3}\right)}^2}\\ =2\sqrt{3}-\sqrt{{3.5}^2}+\left|1-\sqrt{3}\right|\\ =2\sqrt{3}-5\sqrt{3}+\sqrt{3}-1\\ =-1-2\sqrt{3}\end{array}$

$\begin{array}{l}B=x\sqrt{x}-\frac{x^2-x}{\sqrt{x}+1}\\ =x\sqrt{x}-\frac{\left(x^2-x\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\\ =x\sqrt{x}-\frac{x\left(x-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\\ =x\sqrt{x}-\frac{x\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\\ =x\sqrt{x}-x\left(\sqrt{x}-1\right)\\ =x\sqrt{x}-x\sqrt{x}+x\\ =x\end{array}$