Sách bài tập Toán 9 Bài 3 (Chân trời sáng tạo): Tính chất của phép khai phương

Giải SBT Toán 9 Bài 3: Tính chất của phép khai phương

Bài 1 trang 47 sách bài tập Toán 9 Tập 1: Tính giá trị các biểu thức:

a) $A=\sqrt{64}+\sqrt{{\left(-8\right)}^2};$

b) $B=-\sqrt{{\left(-\frac{3}{7}\right)}^2}+{\left(-\sqrt{\frac{10}{7}}\right)}^2;$

c) $C=\sqrt{{\left(2-\sqrt{5}\right)}^2}+\sqrt{{\left(5-\sqrt{5}\right)}^2};$

d) $D=\sqrt{{\left(-5\right)}^2}+\sqrt{{\left(-3\right)}^4}+\sqrt{2^6}.$

Lời giải:

a) $A=\sqrt{64}+\sqrt{{\left(-8\right)}^2}=8+\left|-8\right|=8+8=16.$

b) $B=-\sqrt{{\left(-\frac{3}{7}\right)}^2}+{\left(-\sqrt{\frac{10}{7}}\right)}^2=-\left|-\frac{3}{7}\right|+\frac{10}{7}$$=-\frac{3}{7}+\frac{10}{7}=\frac{7}{7}=1.$

c) $C=\sqrt{{\left(2-\sqrt{5}\right)}^2}+\sqrt{{\left(5-\sqrt{5}\right)}^2}$

$=\left|2-\sqrt{5}\right|+\left|5-\sqrt{5}\right|=\sqrt{5}-2+5-\sqrt{5}=3$ (do $2<\sqrt{5}<5);$

d) $D=\sqrt{{\left(-5\right)}^2}+\sqrt{{\left(-3\right)}^4}+\sqrt{2^6}$$=\left|-5\right|+\left|{\left(-3\right)}^2\right|+\left|2^3\right|=5+9+8=22.$

Bài 2 trang 47 sách bài tập Toán 9 Tập 1: Viết các biểu thức sau dưới dạng (a là một số).

a) $\sqrt{5}\cdot \sqrt{11};$

b) $\sqrt{\frac{10}{3}}\cdot \sqrt{\frac{3}{5}};$

c) $\sqrt{3}\cdot \sqrt{5}\cdot \sqrt{6};$

d) $\sqrt{\frac{6}{7}}\cdot \sqrt{\mathrm{2,8}}.$

Lời giải:

a) $\sqrt{5}\cdot \sqrt{11}=\sqrt{5\cdot 11}=\sqrt{55}.$

b) $\sqrt{\frac{10}{3}}\cdot \sqrt{\frac{3}{5}}=\sqrt{\frac{10}{3}\cdot \frac{3}{5}}=\sqrt{2}.$

c) $\sqrt{3}\cdot \sqrt{5}\cdot \sqrt{6}=\sqrt{3\cdot 5\cdot 6}=\sqrt{90}.$

d) $\sqrt{\frac{6}{7}}\cdot \sqrt{\mathrm{2,8}}=\sqrt{\frac{6}{7}}\cdot \sqrt{\frac{14}{5}}=\sqrt{\frac{6}{7}\cdot \frac{14}{5}}=\sqrt{\frac{12}{5}}=\sqrt{\mathrm{2,4}}.$

Bài 3 trang 47 sách bài tập Toán 9 Tập 1: Rút gọn biểu thức bằng cách đưa thừa số ra ngoài dấu căn.

a) $\sqrt{3\cdot 8^2};$

b) $\sqrt{150};$

c) $\sqrt{1000};$

d) $\sqrt{2^2\cdot 5^4\cdot 7}.$

Lời giải:

a) $\sqrt{3\cdot 8^2}=\left|8\right|\sqrt{3}=8\sqrt{3}.$

b) $\sqrt{150}=\sqrt{5^2\cdot 6}=\left|5\right|\sqrt{6}=5\sqrt{6}.$

c) $\sqrt{1000}=\sqrt{{10}^2\cdot 10}=\left|10\right|\sqrt{10}=10\sqrt{10}.$

d) $\sqrt{2^2\cdot 5^4\cdot 7}=\sqrt{2^2\cdot {\left(5^2\right)}^2\cdot 7}=\sqrt{\left(2\cdot 5^2\right)\cdot 7}$$=\left|2\cdot 5^2\right|\sqrt{7}=2\cdot 5^2\sqrt{7}=50\sqrt{7}.$

Bài 4 trang 47 sách bài tập Toán 9 Tập 1: Đưa thừa số vào trong dấu căn.

a) $6\sqrt{5};$

b) $-8\sqrt{10};$

c) $5\sqrt{\frac{2}{5}};$

d) $4ab\sqrt{\frac{5a}{2 b}}$ với a ≥ 0; b > 0

Lời giải:

a) $6\sqrt{5}=\sqrt{6^2\cdot 5}=\sqrt{36\cdot 5}=\sqrt{180}.$

b) $-8\sqrt{10}=-\sqrt{8^2\cdot 10}=-\sqrt{64\cdot 10}=-\sqrt{640}.$

c) $5\sqrt{\frac{2}{5}}=\sqrt{5^2\cdot \frac{2}{5}}=\sqrt{10}.$

d) Với a ≥ 0; b > 0, ta có: $4ab\sqrt{\frac{5a}{2 b}} = \sqrt{4^2{a}^2{b}^2.\frac{5a}{2b}} = \sqrt{40a^{3}b}$

Bài 5 trang 47 sách bài tập Toán 9 Tập 1: Tính:

a) $\sqrt{\frac{16}{121}};$

b) $\sqrt{4\frac{21}{25}};$

c) $\sqrt{\frac{\mathrm{6,4}}{\mathrm{8,1}}};$

d) $\frac{\sqrt{300}}{\sqrt{27}};$

e) $\frac{\sqrt{6}}{\sqrt{150}};$

g) $\sqrt{\frac{3}{2}}:\sqrt{\frac{1}{24}}.$

Lời giải:

a) $\sqrt{\frac{16}{121}}=\sqrt{\frac{4^2}{{11}^2}}=\frac{\sqrt{4^2}}{\sqrt{{11}^2}}=\frac{4}{11}.$

b) $\sqrt{4\frac{21}{25}}=\sqrt{\frac{121}{25}}=\sqrt{\frac{{11}^2}{5^2}}=\frac{\sqrt{{11}^2}}{\sqrt{5^2}}=\frac{11}{5}.$

c) $\sqrt{\frac{\mathrm{6,4}}{\mathrm{8,1}}}=\sqrt{\frac{\mathrm{6,4}\cdot 10}{\mathrm{8,1}\cdot 10}}=\sqrt{\frac{64}{81}}=\sqrt{\frac{8^2}{9^2}}=\frac{\sqrt{8^2}}{\sqrt{9^2}}=\frac{8}{9}.$

d) $\frac{\sqrt{300}}{\sqrt{27}}=\sqrt{\frac{300}{27}}=\sqrt{\frac{100\cdot 3}{9\cdot 3}}=\sqrt{\frac{100}{9}}=\sqrt{\frac{{10}^2}{3^2}}=\frac{\sqrt{{10}^2}}{\sqrt{3^2}}=\frac{10}{3}.$

e) $\frac{\sqrt{6}}{\sqrt{150}}=\sqrt{\frac{6}{150}}=\sqrt{\frac{6}{25\cdot 6}}=\sqrt{\frac{1}{25}}=\sqrt{{\left(\frac{1}{5}\right)}^2}=\frac{1}{5}.$

g) $\sqrt{\frac{3}{2}}:\sqrt{\frac{1}{24}}=\sqrt{\frac{3}{2}:\frac{1}{24}}=\sqrt{\frac{3}{2}\cdot 24}=\sqrt{36}=\sqrt{6^2}=6.$

Bài 6 trang 47 sách bài tập Toán 9 Tập 1: Tính:

a) $\sqrt{{74}^2-{70}^2};$

b) $\sqrt{{\left(\mathrm{62,5}\right)}^2-{\left(\mathrm{58,5}\right)}^2}+\left(\sqrt{11}-2\sqrt{5}\right)\left(2\sqrt{5}+\sqrt{11}\right).$

Lời giải:

a) $\sqrt{{74}^2-{70}^2}=\sqrt{\left(74+70\right)\left(74-70\right)}$

$=\sqrt{144\cdot 4}=\sqrt{144}\cdot \sqrt{4}=$$\sqrt{{12}^2}\cdot \sqrt{2^2}=12\cdot 2=24.$

b) $\sqrt{{\left(\mathrm{62,5}\right)}^2-{\left(\mathrm{58,5}\right)}^2}+\left(\sqrt{11}-2\sqrt{5}\right)\left(2\sqrt{5}+\sqrt{11}\right)$

$=\sqrt{\left(\mathrm{62,5}+\mathrm{58,5}\right)\left(\mathrm{62,5}-\mathrm{58,5}\right)}+{\left(\sqrt{11}\right)}^2-{\left(2\sqrt{5}\right)}^2$

$=\sqrt{121\cdot 4}+11-2^2\cdot {\left(\sqrt{5}\right)}^2$

$=\sqrt{{11}^2}\cdot \sqrt{2^2}+11-4\cdot 5$

= 11.2 + 11 ‒ 20 = 13.

Bài 7 trang 47 sách bài tập Toán 9 Tập 1: Tính:

a) $\sqrt{24}:\sqrt{2}\cdot \sqrt{3};$

b) $\sqrt{27}\cdot \sqrt{50}:\sqrt{6};$

c) $\sqrt{32}:\frac{2\sqrt{2}}{\sqrt{5}}:\left(-\sqrt{45}\right);$

d) $\frac{\sqrt{\mathrm{8,5}}\cdot \sqrt{\mathrm{15,3}}}{\sqrt{\mathrm{0,45}}}.$

Lời giải:

a) $\sqrt{24}:\sqrt{2}\cdot \sqrt{3}=\sqrt{24:2\cdot 3}=$$\sqrt{12\cdot 3}=\sqrt{36}=\sqrt{6^2}=6.$

b) $\sqrt{27}\cdot \sqrt{50}:\sqrt{6}=\sqrt{27\cdot 50:6}=$$\sqrt{1350:6}=\sqrt{225}=\sqrt{{15}^2}=15.$

c) $\sqrt{32}:\frac{2\sqrt{2}}{\sqrt{5}}:\left(-\sqrt{45}\right)=\sqrt{4^2\cdot 2}\cdot \frac{\sqrt{5}}{2\sqrt{2}}\cdot \frac{1}{-\sqrt{45}}$

$=4\sqrt{2}\cdot \frac{\sqrt{5}}{2\sqrt{2}}\cdot \frac{-1}{\sqrt{3^2\cdot 5}}$$=2\sqrt{5}\cdot \frac{-1}{3\sqrt{5}}=-\frac{2}{3}.$

d) $\frac{\sqrt{\mathrm{8,5}}\cdot \sqrt{\mathrm{15,3}}}{\sqrt{\mathrm{0,45}}}=\sqrt{\frac{\mathrm{8,5}\cdot \mathrm{15,3}}{\mathrm{0,45}}}=\sqrt{\frac{\left(\mathrm{8,5}\cdot 10\right)\cdot \left(\mathrm{15,3}\cdot 10\right)}{\mathrm{0,45}\cdot 100}}$

$=\sqrt{\frac{85\cdot 153}{45}}=\sqrt{\frac{5\cdot 17\cdot 9\cdot 17}{5\cdot 9}}=\sqrt{{17}^2}=17.$

Bài 8 trang 47 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

a) $2\sqrt{a^2}-3a$ với a ≤ 0;

b) $a-\sqrt{a^2-2a+1}$ với a > 1;

c) $\sqrt{4a^2-4a+1}+\sqrt{a^2+6a+9}$ với $-3<a<\frac{1}{2}.$

Lời giải:

a) Với với a ≤ 0, ta có:

$2\sqrt{a^2}-3a=2\left|a\right|-3a=2\cdot \left(-a\right)-3a=-2a-3a=-5a.$

b) Ta có: $a-\sqrt{a^2-2a+1}=a-\sqrt{{\left(a-1\right)}^2}=a-\left|a-1\right|.$

Do a > 1 nên a ‒1 > 0, suy ra |a – 1| = a – 1.

Do đó, $a-\sqrt{a^2-2a+1}=a-\left(a-1\right)=a-a+1=a.$

c) $\sqrt{4a^2-4a+1}+\sqrt{a^2+6a+9}$

$=\sqrt{{\left(2a\right)}^2-2\cdot 2a\cdot 1+1}+\sqrt{a^2+2\cdot a\cdot 3+3^2}$

$=\sqrt{{\left(2a-1\right)}^2}+\sqrt{{\left(a+3\right)}^2}=\left|2a-1\right|+\left|a+3\right|.$

Do $-3<a<\frac{1}{2}$ nên a + 3 > 0 và $a-\frac{1}{2}<0$ hay 2a ‒ 1 < 0.

Suy ra |a + 3| = a + 3 và |2a – 1| = 1 – 2a.

Khi đó, $\sqrt{4a^2-4a+1}+\sqrt{a^2+6a+9}=$$\left|2a-1\right|+\left|a+3\right|=1-2a+a+3=4-a.$

Bài 9 trang 47 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

a) $\sqrt{4{\left(a-3\right)}^2}-a$ với a ≥ 3;

b) $\sqrt{12ab\cdot 3ab}$ (a ≥ 0; b ≤ 0);

c) $\sqrt{5a}\cdot \sqrt{15 b}\cdot \sqrt{27ab}$ (a ≥ 0; b ≥ 0);

d) $\sqrt{9a^2{\left(a-1\right)}^2}$ (0 < a < 1).

Lời giải:

a) Ta có: $\sqrt{4{\left(a-3\right)}^2}-a=2\left|a-3\right|-a.$

Do a ≥ 3 nên a ‒ 3 ≥ 0, suy ra |a – 3| = a – 3.

Khi đó, $\sqrt{4{\left(a-3\right)}^2}-a=2\left(a-3\right)-a$$=2a-6-a=a-6.$

b) $\sqrt{12ab\cdot 3ab}=\sqrt{36a^2{b}^2}=\sqrt{6^2}\cdot \sqrt{a^2}\cdot \sqrt{b^2}=$$6\cdot \left|a\right|\cdot \left|b\right|=6\cdot a\cdot \left(-b\right)=-6ab.$

c) $\sqrt{5a}\cdot \sqrt{15 b}\cdot \sqrt{27ab}=\sqrt{5a\cdot 15b\cdot 27ab}$

$=\sqrt{5\cdot 3\cdot 5\cdot 3\cdot 9\cdot a^2\cdot b^2}$$=\sqrt{5^2\cdot 9^2\cdot a^2\cdot b^2}$

$=45\cdot \left|a\right|\cdot \left|b\right|=45\cdot a\cdot b=45ab.$

d) $\sqrt{9a^2{\left(a-1\right)}^2}=\sqrt{{\left(3a\right)}^2{\left(a-1\right)}^2}=\left|3a\right|\cdot \left|a-1\right|$

Do 0 < a < 1 nên a > 0 và a ‒ 1 < 0.

Suy ra |a| = a và |a – 1| = 1 – a.

Khi đó, $\sqrt{9a^2{\left(a-1\right)}^2}=3a\left(1-a\right)=3a-3a^2.$

Bài 10 trang 47 sách bài tập Toán 9 Tập 1: Tính giá trị của biểu thức $A=\sqrt{\mathrm{0,01}{x}^4{y}^6}$ khi x = 5; y = 4.

Lời giải:

Ta có: $A=\sqrt{\mathrm{0,01}{x}^4{y}^6}=\sqrt{{\left(\mathrm{0,1}\right)}^2\cdot {\left(x^2\right)}^2\cdot {\left(y^3\right)}^2}$

$=\sqrt{{\left(\mathrm{0,1}\right)}^2}\cdot \sqrt{{\left(x^2\right)}^2}\cdot \sqrt{{\left(y^3\right)}^2}=\mathrm{0,1}\cdot \left|x^2\right|\cdot \left|y^3\right|=\mathrm{0,1}{x}^2{y}^3.$

Thay x = 5; y = 4 vào biểu thức trên, ta được:

A = 0,1 . 5² . 4³ = 0,1 . 25 . 64 = 160.

Bài 11 trang 48 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

a) $\frac{\sqrt{5a^3}}{\sqrt{80a}}$ (a > 0);

b) $\frac{6a}{b}\sqrt{\frac{b^2}{9a^4}}$ (a ≠ 0, b ≤ 0);

c) $\sqrt{\frac{4a^2-4a+1}{a^2}}$ với $0<a<\frac{1}{2};$

d) $\left(a-b\right)\cdot \sqrt{\frac{ab}{{\left(a-b\right)}^2}}$ với a < b < 0.

Lời giải:

a) Với a > 0, ta có: $\frac{\sqrt{5a^3}}{\sqrt{80a}}=\sqrt{\frac{5a^3}{80a}}=\sqrt{\frac{a^2}{16}}=\frac{\sqrt{a^2}}{\sqrt{16}}=\frac{\left|a\right|}{4}=\frac{a}{4}.$

b) Với a ≠ 0, b ≠ 0, ta có: $\frac{6a}{b}\sqrt{\frac{b^2}{9a^4}}=\frac{6a}{b}\cdot \frac{\sqrt{b^2}}{\sqrt{3^2\cdot {\left(a^2\right)}^2}}=\frac{6a}{b}\cdot \frac{\left|b\right|}{3\left|a^2\right|}$

Với a ≠ 0, b < 0 ta có |b| = – b và |a²| = a².

Khi đó, $\frac{6a}{b}\sqrt{\frac{b^2}{9a^4}}=\frac{6a}{b}\cdot \frac{\left|b\right|}{3\left|a^2\right|}=\frac{6a}{b}\cdot \frac{-b}{3a^2}=-\frac{2}{a}.$

c) Với a ≠ 0, ta có: $\sqrt{\frac{4a^2-4a+1}{a^2}}=\frac{\sqrt{{\left(2a-1\right)}^2}}{\sqrt{a^2}}=\frac{\left|2a-1\right|}{\left|a\right|}.$

Do $0<a<\frac{1}{2}$ nên a > 0 và $a-\frac{1}{2}<0$ hay 2a ‒ 1 < 0.

Suy ra |a| = a và |2a – 1| = 1 – 2a.

Khi đó, $\sqrt{\frac{4a^2-4a+1}{a^2}}=\frac{\left|2a-1\right|}{\left|a\right|}=\frac{1-2a}{a}.$

d) Với a < b < 0, ta có:

$\left(a-b\right)\cdot \sqrt{\frac{ab}{{\left(a-b\right)}^2}}=\left(a-b\right)\cdot \frac{\sqrt{ab}}{\sqrt{{\left(a-b\right)}^2}}=\left(a-b\right)\cdot \frac{\sqrt{ab}}{\left|a-b\right|}.$

Do a < b < 0 nên a ‒ b < 0, suy ra |a – b| = – (a – b).

Khi đó, $\left(a-b\right)\cdot \sqrt{\frac{ab}{{\left(a-b\right)}^2}}=\left(a-b\right)\cdot \frac{\sqrt{ab}}{\left|a-b\right|}=\left(a-b\right)\cdot \frac{\sqrt{ab}}{-\left(a-b\right)}=-\sqrt{ab}.$

Bài 12 trang 48 sách bài tập Toán 9 Tập 1: Tìm x, biết:

a) $\sqrt{2}\cdot x-\sqrt{50}=0;$

b) $2\sqrt{5}\cdot x+\sqrt{40}=0;$

c) $\frac{3x}{\sqrt{2}}-2\sqrt{18}=0.$

Lời giải:

a) $\sqrt{2}\cdot x-\sqrt{50}=0$

$\sqrt{2}\cdot x=\sqrt{50}$

$x=\frac{\sqrt{50}}{\sqrt{2}}$

$x=\sqrt{\frac{50}{2}}$

$x=\sqrt{25}$

x = 5.

Vậy x = 5.

b) $2\sqrt{5}\cdot x+\sqrt{40}=0$

$2\sqrt{5}\cdot x=-\sqrt{40}$

$x=-\frac{\sqrt{40}}{2\sqrt{5}}$

$x=-\frac{\sqrt{40}}{\sqrt{2^2\cdot 5}}$

$x=-\sqrt{\frac{40}{20}}$

$x=-\sqrt{2}.$

Vậy $x=-\sqrt{2}.$

c) $\frac{3x}{\sqrt{2}}-2\sqrt{18}=0$

$\frac{3x}{\sqrt{2}}=2\sqrt{18}$

$3x=2\sqrt{18}\cdot \sqrt{2}$

$3x=2\sqrt{18\cdot 2}$

$3x=2\sqrt{36}$

3x = 2.6

3x = 12

x = 4.

Vậy x = 4

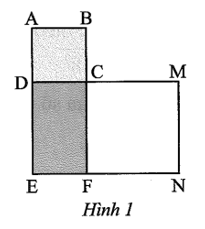
Bài 13 trang 48 sách bài tập Toán 9 Tập 1: Cho Hình 1. Biết ABCD là hình vuông có diện tích bằng 6, CMNF là hình vuông có diện tích bằng 18. Tính diện tích hình chữ nhật CDEF.

Lời giải:

⦁ Ta có công thức tính diện tích của hình vuông ABCD là CD².

Theo bài, ABCD là hình vuông có diện tích bằng 6, nên ta có:

CD² = 6, suy ra $CD=\sqrt{6}$ (do CD > 0).

⦁ Ta có công thức tính diện tích của hình vuông CMNF là CF².

Theo bài, CMNF là hình vuông có diện tích bằng 18, nên ta có:

CF² = 18, suy ra $CD=\sqrt{18}=\sqrt{3^2\cdot 2}=3\sqrt{2}$ (do CF > 0).

⦁ Diện tích hình chữ nhật CDEF là:

$CD\cdot CF=3\sqrt{2}\cdot \sqrt{6}=3\sqrt{2}\cdot \sqrt{2}\cdot \sqrt{3}=$$3\cdot {\left(\sqrt{2}\right)}^2\cdot \sqrt{3}=3\cdot 2\cdot \sqrt{3}=6\sqrt{3}.$

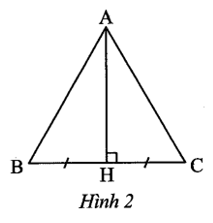
Bài 14 trang 48 sách bài tập Toán 9 Tập 1: Cho Hình 2. Biết tam giác đều ABC có độ dài đường cao AH bằng $11\sqrt{3}.$ Tính độ dài cạnh của tam giác đó.

Lời giải:

Gọi x là độ dài tam giác ABC (x > 0). Khi đoa, AB = BC = CA = x.

Do tam giác ABC đều có AH là đường cao nên đồng thời là đường trung tuyến, suy ra H là trung điểm của BC, do đó $BH=HC=\frac{BC}{2}=\frac{x}{2}.$

Tam giác ABH vuông tại H, theo định lí Pythagore, ta có:

AB² = AH² + BH²

Suy ra $x^2={\left(11\sqrt{3}\right)}^2+{\left(\frac{x}{2}\right)}^2$

$x^2={11}^2\cdot {\left(\sqrt{3}\right)}^2+\frac{x^2}{4}$

4x² = 4.121.3 + x²

3x² = 1 452

x² = 484

x = 22 (do x > 0).

Vậy độ dài cạnh của tam giác đó là 22.

Lý thuyết Tính chất của phép khai phương

1. Căn thức bậc hai của một bình phương

Tính chất

Với biểu thức A bất kì, ta có $\sqrt{A^2}=\left|A\right|$, nghĩa là $\sqrt{A^2}=A$ khi $A\ge 0$; $\sqrt{A^2}=-A$ khi $A<0$.

Ví dụ: Với $x<0$, ta có 1 – x > 0. Do đó ${\left(\sqrt{1-x}\right)}^2=1-x$.

2. Căn thức bậc hai của một tích

Với hai biểu thức A và B nhận giá trị không âm, ta có $\sqrt{A}.\sqrt{B}=\sqrt{AB}$.

Ví dụ:

$\sqrt{27}.\sqrt{3}=\sqrt{27.3}=\sqrt{81}=9$

Với $a\ge 0,b<0$ thì $\sqrt{25a^2{b}^2}=\sqrt{5^2.a^2.{\left(-b\right)}^2}=\sqrt{5^2}.\sqrt{a^2}.\sqrt{{\left(-b\right)}^2}=5.a.\left(-b\right)=-5ab$.

Nhận xét: Ta có thể biến đổi $\sqrt{ab}=\sqrt{a}.\sqrt{b}$ hoặc $\sqrt{a}.\sqrt{b}=\sqrt{ab}$ ($a\ge 0$ và $b\ge 0$) để việc tính toán được dễ dàng hơn.

Với số thực a bất kì và b không âm, ta có $\sqrt{a^{2}b}=\left|a\right|\sqrt{b}$. Biến đổi này được gọi là đưa thừa số ra ngoài dấu căn. Ngược lại, ta có biến đổi đưa thừa số vào trong dấu căn. + Nếu $a\ge 0$ thì $a\sqrt{b}=\sqrt{a^{2}b}$. + Nếu $a<0$ thì $a\sqrt{b}=-\sqrt{a^{2}b}$.

Tổng quát, với hai biểu thức A và B mà $B\ge 0$, ta có $\sqrt{A^{2}B}=\left|A\right|\sqrt{B}$.

Ví dụ:

$\sqrt{75}=\sqrt{25.3}=\sqrt{5^2.3}=5\sqrt{3}$

$\sqrt{15a}.\sqrt{3a}=\sqrt{15a.3a}=\sqrt{3^2{a}^2.5}=\left|3a\right|\sqrt{5}$.

2. Căn thức bậc hai của một thương

Tính chất

Với biểu thức A nhận giá trị không âm và biểu thức B nhận giá trị dương, ta có $\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}$.

Ví dụ: $\sqrt{\frac{49}{64}}=\frac{\sqrt{49}}{\sqrt{64}}=\frac{7}{8}$;

$\sqrt{\frac{4a^2}{25}}=\frac{\sqrt{4a^2}}{\sqrt{25}}=\frac{\sqrt{4}.\sqrt{a^2}}{\sqrt{25}}=\frac{2\left|a\right|}{5}$;

$\frac{\sqrt{8}}{\sqrt{2}}=\sqrt{\frac{8}{2}}=\sqrt{4}=2$;

Với $a>0$ thì $\frac{\sqrt{52a^3}}{\sqrt{13a}}=\sqrt{\frac{52a^3}{13a}}=\sqrt{4a^2}=\sqrt{{\left(2a\right)}^2}=2a$.

Nhận xét: Ta có thể biến đổi $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$ hoặc $\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$ ($a\ge 0$ và $b\ge 0$) để việc tính toán được dễ dàng hơn.