Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 9 Bài 2 (Chân trời sáng tạo): Hệ thức giữa cạnh và góc của tam giác vuông

    Với giải sách bài tập Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 9 Bài 2.

    1 448 03/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông

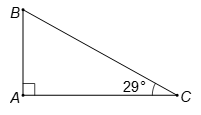
    Bài 1 trang 72 sách bài tập Toán 9 Tập 1: Cho tam giác vuông có cạnh huyền bằng 25 cm, một góc nhọn bằng 29°. Tính các cạnh còn lại của tam giác đó.

    Cho tam giác vuông có cạnh huyền bằng 25 cm, một góc nhọn bằng 29°. Tính các cạnh còn lại của tam giác đó

    Lời giải:

    Gọi tam giác ABC là tam giác vuông tại A có BC = 25 cm và C^=29°.

    Ta có: AB = BC.sinC = 25.sin29° ≈ 12,12 (cm);

    AC = BC.cosC = 25.cos29° ≈ 21,87 (cm).

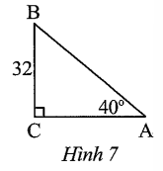
    Bài 2 trang 72 sách bài tập Toán 9 Tập 1: Tính cạnh AC của tam giác vuông trong Hình 7.

    Tính cạnh AC của tam giác vuông trong Hình 7 trang 72 sách bài tập Toán 9 Tập 1

    Lời giải:

    Xét ∆ABC vuông tại C có:

    AC = BC.cotA = 32.cot 40° ≈ 38,14.

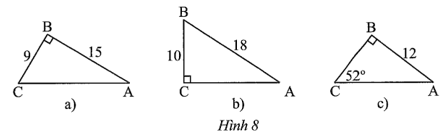
    Bài 3 trang 72 sách bài tập Toán 9 Tập 1: Giải tam giác vuông ABC trong mỗi trường hợp sau:

    Giải tam giác vuông ABC trong mỗi trường hợp sau trang 72 sách bài tập Toán 9 Tập 1

    Lời giải:

    a) Áp dụng định lí Pythagore cho tam giác ABC vuông tại B, ta có:

    AC=BA2+BC2=152+92=306≈17,49.

    Xét ∆ABC vuông tại B, ta có:

    ⦁ tanA=BCBA=915=0,6, suy ra A^≈30°58'.

    ⦁ A^+C^=90° (tổng hai góc nhọn trong tam giác vuông bằng 90°)

    Suy ra C^=90°−A^≈90°−30°58'=59°2'.

    b) Áp dụng định lí Pythagore cho tam giác ABC vuông tại C, ta có:

    AC=AB2−BC2=182−102=224≈14,97.

    Xét ∆ABC vuông tại C, ta có:

    ⦁ sinA=BCAB=1018=59, suy ra A^≈33°45'.

    ⦁ A^+B^=90° (tổng hai góc nhọn trong tam giác vuông bằng 90°)

    Suy ra B^=90°−A^≈90°−33°45'=56°15'.

    c) Xét ∆ABC vuông tại B, ta có:

    ⦁ A^+C^=90° (tổng hai góc nhọn trong tam giác vuông bằng 90°)

    Suy ra A^=90°−C^=90°−52°=38°.

    ⦁ BC = AB.tanA = 12.tan38° ≈ 9,38.

    ⦁ AB = AC.sinC, suy ra AC=ABsinC=12sin52°≈15,23.

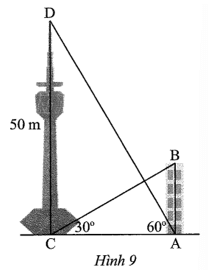
    Bài 4 trang 72 sách bài tập Toán 9 Tập 1: Từ chân một tháp cao 50 m người ta nhìn thấy đỉnh của một tòa nhà với góc nâng 30°. Trong khi đó từ chân tòa nhà, người ta lại nhìn thấy đỉnh tháp với góc nâng 60°. Tính chiều cao của tòa nhà.

    Từ chân một tháp cao 50 m người ta nhìn thấy đỉnh của một tòa nhà với góc nâng 30°

    Lời giải:

    Ta có chiều cao của tòa nhà và tháp lần lượt là AB, CD (đơn vị: m, AB > 0).

    Khi đó, ACB^=30°,CAD^=60°.

    Xét tam giác ACD vuông tại C, ta có:

    AC=DC⋅cotCAD^=50⋅cot60°=5033  (m).

    Xét tam giác ABC vuông tại A, ta có:

    AB=AC⋅tanACB^=5033⋅tan30°=5033⋅33=503≈16,67  (m).

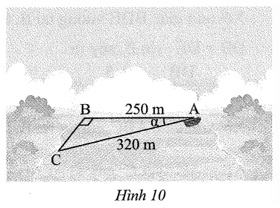
    Bài 5 trang 72 sách bài tập Toán 9 Tập 1: Tại khúc sông rộng 250 m, một chiếc thuyền đang đậu tại vị trí A và muốn di chuyển đến vị trí B bên kia bờ sông (Hình 10). Tuy nhiên, do chịu ảnh hưởng của dòng nước nên thuyền đã di chuyển đến vị trí C. Hãy xác định xem dòng nước đã làm chiếc thuyền đó di chuyển lệch đi một góc bao nhiêu độ so với dự tính ban đầu.

    Tại khúc sông rộng 250 m, một chiếc thuyền đang đậu tại vị trí A và muốn di chuyển đến vị trí B

    Lời giải:

    Xét tam giác ABC vuông tại B, ta có:

    cosBAC^=ABAC=250320=0,78125, suy ra BAC^≈38°37'.

    Vậy chiếc thuyền đó bị dòng nước đẩy lệch một góc khoảng 38°37’ so với dự tính.

    Lý thuyết Hệ thức giữa cạnh và góc của tam giác vuông

    1. Hệ thức giữa cạnh và góc của tam giác vuông

    Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn

    Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

    Cạnh góc vuông = (cạnh huyền ) × (sin góc đối)

    = (cạnh huyền ) × (cosin góc kề)

    Ví dụ 1:

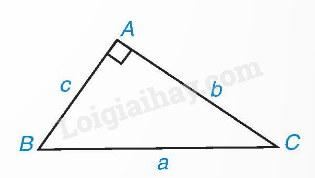
    Lý thuyết Hệ thức giữa cạnh và góc của tam giác vuông (Chân trời sáng tạo 2024) | Lý thuyết Toán 9 (ảnh 1)

    Trong tam giác ABC vuông tại A, ta có:

    b=a.sin⁡B=a.cos⁡C;c=a.sin⁡C=a.cos⁡B.

    Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn

    Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc côtang góc kề.

    Cạnh góc vuông = (cạnh góc vuông còn lại ) × (tan góc đối)

    = (cạnh góc vuông còn lại ) × (cot góc kề)

    Ví dụ 2:

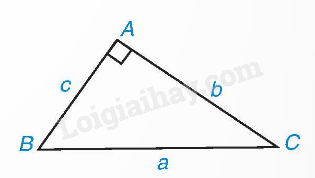
    Lý thuyết Hệ thức giữa cạnh và góc của tam giác vuông (Chân trời sáng tạo 2024) | Lý thuyết Toán 9 (ảnh 2)

    Trong tam giác ABC vuông tại A, ta có:

    b=c.tan⁡B=c.cot⁡C;c=b.tan⁡C=b.cot⁡B.

    2. Giải tam giác vuông

    Giải tam giác vuông là tính các cạnh và góc chưa biết của tam giác đó.

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 448 03/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: