Sách bài tập Toán 9 Bài 2 (Chân trời sáng tạo): Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

Giải SBT Toán 9 Bài 2: Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

Bài 1 trang 10 sách bài tập Toán 9 Tập 1: Trong các cặp số (1; 1), (–2; –4), (–2; 6), $\left(3;-\frac{1}{4}\right),$ cặp số nào là nghiệm của mỗi phương trình sau?

a) 5x + 3y = 8;

b) 3x – 4y = 10.

Lời giải:

a) Xét phương trình 5x + 3y = 8.

⦁ Cặp số (1; 1) là nghiệm của phương trình vì

5.1 + 3.1 = 5 + 3 = 8.

⦁ Cặp số (–2; –4) không là nghiệm của phương trình vì

5.(–2) + 3.(–4) = ‒ 10 ‒ 12 = – 22 ≠ 8.

⦁ Cặp số (–2; 6) là nghiệm của phương trình vì

5.(–2) + 3.6 = ‒10 + 18 = 8.

⦁ Cặp số $\left(3;-\frac{1}{4}\right)$ không là nghiệm của phương trình vì

$5\cdot 3+3\cdot \left(-\frac{1}{4}\right)=15-\frac{3}{4}=\frac{60}{4}-\frac{3}{4}=\frac{57}{4}\ne 8.$

b) Xét phương trình 3x – 4y = 10.

⦁ Cặp số (1; 1) không là nghiệm của phương trình vì

3.1 – 4.1 = 3 ‒4 = –1 ≠ 10.

⦁ Cặp số (–2; –4) là nghiệm của phương trình vì

3.(–2) – 4.(–4) = ‒6 + 16 = 10.

⦁ Cặp số (–2; 6) không là nghiệm của phương trình vì

3.(–2) – 4.6 = ‒6 ‒ 24 = –30 ≠ 10.

⦁ Cặp số $\left(3;-\frac{1}{4}\right)$ là nghiệm của phương trình vì

$3\cdot 3-4\cdot \left(-\frac{1}{4}\right)=9+1=10.$

Bài 2 trang 10 sách bài tập Toán 9 Tập 1: Cho hệ phương trình $\left\{\begin{array}{l}3x+2y=7\\ -x-4y=-9.\end{array}\right.$ Trong các cặp số (3; 2), (1; 2), (5; 1), cặp số nào là nghiệm của hệ phương trình đã cho?

Lời giải:

Xét hệ phương trình $\left\{\begin{array}{l}3x+2y=7\\ -x-4y=-9.\end{array}\right.$

⦁ Cặp số (3; 2) không là nghiệm của hệ phương trình vì $\left\{\begin{array}{l}3\cdot 3+2\cdot 2=13\left(\ne 7\right)\\ -3-4\cdot 2=-11\left(\ne -9\right).\end{array}\right.$

⦁ Cặp số (1; 2) là nghiệm của hệ phương trình vì $\left\{\begin{array}{l}3\cdot 1+2\cdot 2=7\\ -1-4\cdot 2=-9.\end{array}\right.$

⦁ Cặp số (5; 1) không là nghiệm của hệ phương trình vì $\left\{\begin{array}{l}3\cdot 5+2\cdot 1=17\left(\ne 7\right)\\ -5-4\cdot 1=-9.\end{array}\right.$

Bài 3 trang 10 sách bài tập Toán 9 Tập 1: Biểu diễn tất cả các nghiệm của mỗi phương trình sau trên mặt phẳng toạ độ Oxy.

a) 2x + y = –2;

b) 0x – y = –3;

c) –4x + 0y = 6.

Lời giải:

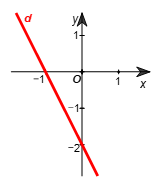
a) Viết lại phương trình thành y = ‒2x ‒ 2.

Tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = ‒2x ‒ 2.

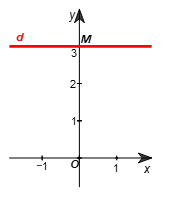
b) Viết lại phương trình thành y = 3.

Tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d vuông góc với Oy tại điểm M(0; 3).

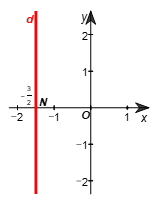
c) Viết lại phương trình thành $x=-\frac{3}{2}.$

Tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d vuông góc với Ox tại điểm $N\left(-\frac{3}{2};0\right).$

Bài 4 trang 11 sách bài tập Toán 9 Tập 1: Cho ba phương trình x + 2y = –1; 2x – y = 7; –x + 3y = –9. Hãy lập một hệ hai phương trình bậc nhất hai ẩn từ ba phương trình đã cho sao cho hệ nhận cặp số (3; –2) làm nghiệm.

Lời giải:

Hệ hai phương trình bậc nhất hai ẩn từ ba phương trình đã cho sao cho hệ nhận cặp số (3; –2) làm nghiệm nên cặp số phải là nghiệm của ít nhất 2 trong 3 phương trình đã cho.

Thay x = 3; y = ‒2 lần lượt vào từng phương trình ta có:

⦁ 3 + 2.(‒2) = 3 ‒ 4 = ‒1.

Do đó cặp số (3; –2) là nghiệm của phương trình x + 2y = –1.

⦁ 2.3 ‒ (‒2) = 6 + 2 = 8 ≠ 7.

Do đó cặp số (3; –2) không là nghiệm của phương trình 2x – y = 7.

⦁ ‒ 3 + 3.(‒2) = ‒ 3 ‒ 6 = ‒9.

Do đó cặp số (3; –2) là nghiệm của phương trình –x + 3y = –9.

Vậy hệ hai phương trình bậc nhất hai ẩn từ ba phương trình đã cho sao cho hệ nhận cặp số (3 ;–2) làm nghiệm là: $\left\{\begin{array}{l}x+2y=-1\\ -x+3y=-9.\end{array}\right.$

Bài 5 trang 11 sách bài tập Toán 9 Tập 1: Cho hai đường thẳng $y=-\frac{1}{2}x-3$ và y = –3x + 2. Vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm A của hai đường thẳng và cho biết toạ độ của điểm A có là nghiệm của hệ phương trình $\left\{\begin{array}{l}\text{x}+2\text{y}=-6\\ 3\text{x}+\text{y}=2\end{array}\right.$ không. Tại sao?

Lời giải:

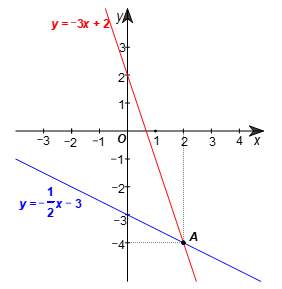
Vẽ hai đường thẳng $y=-\frac{1}{2}x-3$ và y = –3x + 2 trên cùng một hệ trục tọa độ như hình vẽ sau:

Toạ độ giao điểm A của hai đường thẳng là A(2;–4).

Viết lại $y=-\frac{1}{2}x-3$ thành x + 2y = –6.

Viết lại y = –3x + 2 thành 3x + y = 2.

Vậy toạ độ giao điểm A(2 ;–4) là nghiệm của hệ phương trình $\left\{\begin{array}{l}x+2y=-6\\ 3x+y=2.\end{array}\right.$

Lý thuyết Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

1. Phương trình bậc nhất hai ẩn

– Phương trình bậc nhất hai ẩn x và y là hệ thức có dạng

ax + b = c,

trong đó a, b, c là các số đã biết (gọi là hệ số), a và b không đồng thời bằng 0.

Ví dụ 1.

• x + 7y = –1 là phương trình bậc nhất hai ẩn với a = 1, b = 7, c = –1.

• 0x – 0y = 6 không phải là phương trình bậc nhất hai ẩn vì a = 0 và b = 0.

–Nếu giá trị của vế trái tại x = x₀ và y = y₀ bằng vế phải thì cặp số (x₀; y₀) được gọi là một nghiệm của phương trình.

Giải phương trình là tìm tất cả các nghiệm của phương trình đó.

Ví dụ 2. Trong các cặp số (0; 5), (1; 1), (–2; 1), cặp số nào là nghiệm của mỗi phương trình 2x + 5y = 7?

Hướng dẫn giải

a) Cặp số (0; 5) khôngphải là nghiệm của phương trình 2x + 5y = 7 vì 2 . 0 + 5 . 5 = 25≠ 7.

Cặp số (1; 1) là nghiệm của phương trình 2x + 5y = 7 vì 2 . 1 + 5 . 1 = 2 + 5 = 7.

Cặp số (–2; 1) không phải là nghiệm của phương trình 2x + 5y = 7 vì 2 . (–2) + 5 . 1 = 1 ≠ 7.

Vậy trong các cặp số đã cho thì có cặp số (1; 1) là nghiệm của phương trình 2x + 5y = 7.

2. Hệ hai phương trình bậc nhất hai ẩn

– Hệ hai phương trình bậc nhất hai ẩn x, y có dạng:

$\left(\mathrm{I}\right)\left\{\begin{array}{l}\text{ax}+\mathrm{by}=\mathrm{c}\left(1\right)\\ ax+{\mathrm{b}}^{\text{'}}\mathrm{y}={\mathrm{c}}^{\text{'}}.\left(2\right)\end{array}\right.$

Trong đó, a, b, c, a', b', c' là các số đã biết (gọi là hệ số), a và b không đồng thời bằng 0, a' và b' không đồng thời bằng 0.

Ví dụ 3. Hệ phương trình $\left\{\begin{array}{l}x+3y=0\\ 4x-3y=-4\end{array}\right.$là hệ phương trình bậc nhất hai ẩn với a = 1, b = 3, c = 0, a' = 4, b' = –3, c' = –4.

–Nếu (x₀; y₀) là nghiệm chung của hai phương trình (1) và (2) thì (x₀; y₀) được gọi là một nghiệm của hệ (I).

Giải hệ phương trình là tìm tất cả các nghiệm của hệ phương trình đó.

Ví dụ 4. Cho hệ phương trình

$\left\{\begin{array}{l}x+3y=3\\ 2x+y=-4.\end{array}\right.$

Trong hai cặp số (1; 2) và (–3; 2), cặp số nào là nghiệm của hệ phương trình đã cho?

Hướng dẫn giải

• Cặp số (0; 2) không phải là nghiệm của hệ phương trình đã cho vì $\left\{\begin{array}{l}1+3\cdot 2=7\left(\ne 3\right)\\ 2\cdot 1+2=4\left(\ne -4\right).\end{array}\right.$

• Cặp số (–3; 2) là nghiệm của hệ phương trình đã cho vì $\left\{\begin{array}{l}-3+3\cdot 2=3\\ 2\cdot \left(-3\right)+2=-4.\end{array}\right.$

Vậy trong hai cặp số (0; 2) và (–5; 3), cặp số (–5; 3) là nghiệm của hệ phương trình đã cho.