Sách bài tập Toán 9 Bài 1 (Chân trời sáng tạo): Căn bậc hai

Giải SBT Toán 9 Bài 1: Căn bậc hai

Bài 1 trang 40 sách bài tập Toán 9 Tập 1: Tìm các căn bậc hai của các số:

a) 0,81;

b) $\frac{1}{100};$

c)$1\frac{7}{9};$

d) 10⁶.

Lời giải:

a) Ta có 0,9² = 0,81 nên 0,81 có hai căn bậc hai là 0,9 và ‒0,9.

b) Ta có ${\left(\frac{1}{10}\right)}^2=\frac{1}{100}$ nên $\frac{1}{100}$ có hai căn bậc hai là $\frac{1}{10}$ và $\frac{1}{100}$

c) Ta có ${\left(\frac{4}{3}\right)}^2=\frac{16}{9}=1\frac{7}{9},$ nên $1\frac{7}{9}$ có hai căn bậc hai là $\frac{4}{3}$ và $-\frac{4}{3}.$

d) Ta có (10³)² = 10⁶ nên 10⁶ có hai căn bậc hai là 10³ = 1 000 và ‒10³ = ‒1 000.

Bài 2 trang 40 sách bài tập Toán 9 Tập 1: Tìm số có căn bậc hai là:

a) $\sqrt{6};$

b) 0,5;

c) $-\sqrt{16};$

d) $-\frac{1}{2}.$

Lời giải:

a) Ta có: ${\left(\sqrt{6}\right)}^2=6$

Vậy số có căn bậc hai là $\sqrt{6}$ là 6.

b) Ta có: 0,5² = 0,25

Vậy số có căn bậc hai là 0,5 là 0,25.

c) Ta có: ${\left(-\sqrt{16}\right)}^2=16$

Vậy số có căn bậc hai là $-\sqrt{16}$ là 16.

d) Ta có: ${\left(-\frac{1}{2}\right)}^2=\frac{1}{4}$

Vậy số có căn bậc hai là $-\frac{1}{2}$ là $\frac{1}{4}.$

Bài 3 trang 40 sách bài tập Toán 9 Tập 1: Tìm x, biết:

a) x² = 64;

b) 9x² = 1;

c) 4x² = 25.

Lời giải:

a) x² = 64

x² = 8² = (‒8)²

x = 8 hoặc x = ‒8.

Vậy x ∈ {8; ‒8}.

b) 9x² = 1

$x^2=\frac{1}{9}$

$x^2={\left(\frac{1}{3}\right)}^2={\left(-\frac{1}{3}\right)}^2$

$x=\frac{1}{3}$ hoặc $x=-\frac{1}{3}.$

Vậy $x\in \left\{\frac{1}{3};-\frac{1}{3}\right\}.$

c) 4x² = 25

$x^2=\frac{25}{4}$

$x^2={\left(\frac{5}{2}\right)}^2={\left(-\frac{5}{2}\right)}^2$

$x=\frac{5}{2}$ hoặc $x=-\frac{5}{2}.$

Vậy $x\in \left\{\frac{5}{2};-\frac{5}{2}\right\}.$

Bài 4 trang 40 sách bài tập Toán 9 Tập 1: Tìm x, biết:

a) $\sqrt{x}=9;$

b) $\sqrt{x}=\sqrt{5};$

c) $3\sqrt{x}=1$

d) $2\sqrt{x+1}=12.$

Lời giải:

a)

x = 81.

Vậy x = 81.

b) $\sqrt{x}=\sqrt{5}$

${\left(\sqrt{x}\right)}^2={\left(\sqrt{5}\right)}^2$

x = 5.

Vậy x = 5.

c) $3\sqrt{x}=1$

${\left(3\sqrt{x}\right)}^2=1^2$

9x = 1

$x=\frac{1}{9}$

Vậy $x=\frac{1}{9}$

d) $2\sqrt{x+1}=12$

${\left(2\sqrt{x+1}\right)}^2={12}^2$

4(x+1) = 144

x + 1 = 36

x = 35.

Vậy x = 35.

Bài 5 trang 41 sách bài tập Toán 9 Tập 1: Tính giá trị của các biểu thức:

a) ${\left(\sqrt{18}\right)}^2+{\left(-\sqrt{12}\right)}^2;$

b) $\sqrt{{\left(-10\right)}^2}-\sqrt{144};$

c) $\sqrt{9^2}\cdot {\left(-\sqrt{6}\right)}^2;$

d) $\sqrt{\mathrm{0,16}}:{\left(-\sqrt{4}\right)}^2.$

Lời giải:

a) ${\left(\sqrt{18}\right)}^2+{\left(-\sqrt{12}\right)}^2=18+12=30.$

b) $\sqrt{{\left(-10\right)}^2}-\sqrt{144}=10-\sqrt{{12}^2}=10-12=-2.$

c) $\sqrt{9^2}\cdot {\left(-\sqrt{6}\right)}^2=9\cdot 6=54.$

d) $\sqrt{\mathrm{0,16}}:{\left(-\sqrt{4}\right)}^2=\sqrt{{\mathrm{0,4}}^2}:4=\mathrm{0,4}:4=\mathrm{0,1.}$

Bài 6 trang 41 sách bài tập Toán 9 Tập 1: Tính giá trị của các biểu thức:

a) $A=\sqrt{144}-{\left(-\sqrt{11}\right)}^2+4\cdot {\left(\sqrt{\frac{7}{2}}\right)}^2-{\left(-\sqrt{3}\right)}^4;$

b) $B={\left(-\sqrt{12}\right)}^2:\sqrt{16}-\sqrt{\frac{1}{49}}\cdot {\left(\sqrt{7}\right)}^2.$

Lời giải:

a) $A=\sqrt{{12}^2}-11+4\cdot \frac{7}{2}-{\left[{\left(-\sqrt{3}\right)}^2\right]}^2$$=12-11+14-3^2=12-11+14-9=6;$

b) $B=12:\sqrt{4^2}-\sqrt{{\left(\frac{1}{7}\right)}^2}\cdot 7$$=12:4-\frac{1}{7}\cdot 7=3-1=2.$

Bài 7 trang 41 sách bài tập Toán 9 Tập 1: So sánh các cặp số sau:

a) $\sqrt{3}$ và $\sqrt{\frac{5}{2}};$

b) 4 và $\sqrt{15}.$

Lời giải:

a) Ta có: $3=\frac{6}{2}>\frac{5}{2}$ nên $\sqrt{3}>\sqrt{\frac{5}{2}}.$

b) Ta có: 16 > 15 nên $\sqrt{16}>\sqrt{15}$ hay $4>\sqrt{15}.$

Bài 8 trang 41 sách bài tập Toán 9 Tập 1: Sắp xếp các số sau theo thứ tự từ nhỏ đến lớn.

$\frac{1}{5};-\sqrt{3};-\sqrt{\frac{3}{2}};\sqrt{5}.$

Lời giải:

– Ta chia các số trên thành hai nhóm:

+ Nhóm 1: gồm hai số $-\sqrt{3}$ và $-\sqrt{\frac{3}{2}};$

+ Nhóm 2: gồm hai số $\frac{1}{5}$ và $\sqrt{5}.$

– So sánh các số trong nhóm 1: $-\sqrt{3}$ và $-\sqrt{\frac{3}{2}};$

Ta có: $3=\frac{6}{2}>\frac{3}{2}$ nên $\sqrt{3}>\sqrt{\frac{3}{2}},$ suy ra $-\sqrt{3}<-\sqrt{\frac{3}{2}}.$

– So sánh các số trong nhóm 2: $\frac{1}{5}$ và $\sqrt{5}.$

Ta có: $\frac{1}{25}<5$ nên $\sqrt{\frac{1}{25}}<\sqrt{5}$

Mà $\sqrt{\frac{1}{25}}=\sqrt{{\left(\frac{1}{5}\right)}^2}=\frac{1}{5},$ suy ra $\frac{1}{5}<\sqrt{5}.$

Mặt khác, các số trong nhóm 1 là các số âm và các số trong nhóm 2 là các số dương. Do vậy, ta có: $-\sqrt{3}<-\sqrt{\frac{3}{2}}<\frac{1}{5}<\sqrt{5}.$

Vậy sắp xếp các số đã cho theo thứ tự từ nhỏ đến lớn như sau:

$-\sqrt{3};-\sqrt{\frac{3}{2}};\frac{1}{5};\sqrt{5}.$

Bài 9 trang 41 sách bài tập Toán 9 Tập 1: Tìm x để căn thức xác định:

a) $\sqrt{2x+7};$

b) $\sqrt{12-3x};$

c) $\sqrt{\frac{1}{x-4}};$

d) $\sqrt{x^2+1}.$

Lời giải:

a) Biểu thức $\sqrt{2x+7}$ xác định khi 2x + 7 ≥ 0 hay 2x ≥ ‒7, hay $x\ge -\frac{7}{2}.$

b) Biểu thức $\sqrt{12-3x}$ xác định khi 12 ‒ 3x ≥ 0 hay ‒3x ≥ ‒12, hay x ≤ 4.

c) Biểu thức $\sqrt{\frac{1}{x-4}}$ xác định khi $\frac{1}{x-4}\ge 0$ hay x ‒ 4 > 0 (do 1 > 0), hay x > 4.

d) Với mọi x ∈ ℝ, ta luôn có x² ≥ 0, do đó x² + 1 ≥ 1 hay x² + 1 > 0.

Suy ra căn thức $\sqrt{x^2+1}$ xác định với mọi số thực x.

Bài 10 trang 41 sách bài tập Toán 9 Tập 1: Tìm giá trị của biểu thức $A=\sqrt{a^2+9a}$ khi a = 16.

Lời giải:

Với a = 16, ta có a² + 9a = 16² + 9.16 = 256 + 144 = 400.

Khi đó, $A=\sqrt{400}=\sqrt{{20}^2}=20.$

Bài 11 trang 41 sách bài tập Toán 9 Tập 1: Diện tích S của hình tròn bán kính r được tính theo công thức S = πr².

a) Viết công thức tính bán kính r theo diện tích S của hình tròn.

b) Tính bán kính r (cm) của hình tròn có diện tích 20 cm² (kết quả làm tròn đến hàng phần mười của xăngtimét).

Lời giải:

a) Từ S = πr², ta có $r^2=\frac{S}{\pi },$ suy ra $r=\sqrt{\frac{S}{\pi }}$ (do r > 0).

Vậy công thức tính bán kính r theo diện tích S của hình tròn là $r=\sqrt{\frac{S}{\pi }}$

b) Với S = 20 cm², ta có $r=\sqrt{\frac{20}{\pi }}\approx \mathrm{2,5}$ (cm).

Bài 12 trang 41 sách bài tập Toán 9 Tập 1: Thời gian rơi t tính theo giây của một vật được thả rơi tự do từ độ cao h (m) cho đến khi chạm đất thoả mãn hệ thức h = 5t².

a) Tính thời gian rơi của vật khi h = 20 m và khi h = 10 m (kết quả làm tròn đến hàng phần mười của giây).

b) Viết công thức biểu thị thời gian rơi t theo độ cao h (h > 0).

Lời giải:

a) Với h = 20 m, ta có 20 = 5t² hay t² = 4, suy ra t = 2 (giây) (do t > 0).

Với h = 10 m, ta có 10 = 5t² hay t² = 2 suy ra $t=\sqrt{2}\approx \mathrm{1,4}$(giây) (do t > 0).

b) Từ h = 5t², suy ra $t^2=\frac{h}{5},$ suy ra $t=\sqrt{\frac{h}{5}}$ (do t > 0).

Vậy công thức biểu thị thời gian rơi t theo độ cao h (h > 0) là: $t=\sqrt{\frac{h}{5}}.$

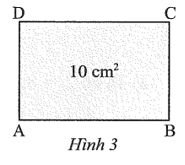
Bài 13 trang 41 sách bài tập Toán 9 Tập 1: Cho hình chữ nhật ABCD có diện tích bằng 10 cm² và tỉ số giữa hai cạnh kề nhau AB : AD = 3 : 2. Tìm độ dài cạnh AB (kết quả làm tròn đến hàng phần mười của xăngtimét).

Lời giải:

Đặt AB = x (cm) (x > 0).

Ta có $\frac{AB}{AD}=\frac{3}{2},$ suy ra $AD=\frac{2AB}{3}=\frac{2x}{3}\text{ (cm).}$

Diện tích hình chữ nhật ABCD là $S=AB\cdot AD=x\cdot \frac{2x}{3}=\frac{2x^2}{3}$ (cm²).

Theo đề bài, hình chữ nhật ABCD có diện tích bằng 10 cm² nên ta có:

$\frac{2x^2}{3}=\mathrm{10,}$ suy ra x² = 15, suy ra $x=\sqrt{15}\approx \mathrm{3,9}$ (cm) (do x > 0).

Vậy độ dài cạnh AB là khoảng 3,9 cm.

Bài 14 trang 41 sách bài tập Toán 9 Tập 1: Tìm tất cả các số tự nhiên n sao cho $\sqrt{9-n}$ là số tự nhiên.

Lời giải:

⦁ Điều kiện xác định của căn thức $\sqrt{9-n}$ là 9 ‒ n ≥ 0 hay n ≤ 9.

⦁ Vì n là số tự nhiên nên n ≥ 0, suy ra ‒ n ≤ 0, do đó 9 ‒ n ≤ 9.

Suy ra 0 ≤ 9 ‒ n ≤ 9.

⦁ Như vậy, để A = $\sqrt{9-n}$ là số tự nhiên thì 9 ‒ n phải nhận các giá trị là số chính phương.

Do đó 9 ‒ n ∈ {0; 1; 4; 9}.

Ta có bảng sau:

Vậy các giá trị cần tìm của n là 9; 8; 5; 0.

Lý thuyết Căn bậc hai

1. Căn bậc hai

Khái niệm căn bậc hai

Cho số thực a không âm. Số thực x thỏa mãn $x^2=a$ được gọi là một căn bậc hai của a.

Chú ý:

- Mỗi số dương a có đúng hai căn bậc hai là hai số đối nhau: số dương là $\sqrt{a}$ (căn bậc hai số học của a) và số âm là $-\sqrt{a}$.

- Số 0 chỉ có đúng một căn bậc hai là chính nó, ta viết $\sqrt{0}=0$.

- Số âm không có căn bậc hai.

- Phép toán tìm căn bậc hai số học của số không âm gọi là phép khai căn bậc hai hay phép khai phương (gọi tắt là khai phương).

­- Nếu $a>b>0$ thì $\sqrt{a}>\sqrt{b}$. Suy ra $-\sqrt{a}<-\sqrt{b}<0<\sqrt{b}<\sqrt{a}$.

Ví dụ:

• $\sqrt{81}=9$ nên 81 có hai căn bậc hai là 9 và -9.
• Căn bậc hai số học của 121 là $\sqrt{121}=11$.

2. Tính căn bậc hai của một số bằng máy tính cầm tay

Để tính các căn bậc hai của một số $a>0$, chỉ cần tính $\sqrt{a}$. Có thể dễ dàng làm điều này bằng cách sử dụng MTCT. Sử dụng nút này để bấm căn bậc hai.

Ví dụ:

Bấm lần lượt các phím ta tính được $\sqrt{9,45}\approx 3,07$.

Vậy căn bậc hai của 9,45 (làm tròn đến chữ số thập phân thứ hai) là 3,07 và -3,07.

Tính chất của căn bậc hai

$\sqrt{a^2}=\left|a\right|$ với mọi số thực a.

Ví dụ: $\sqrt{{\left(1+\sqrt{2}\right)}^2}=\left|1+\sqrt{2}\right|=1+\sqrt{2}$; $\sqrt{{\left(-3\right)}^2}=\left|-3\right|=3$.

3. Căn thức bậc hai

Khái niệm căn thức bậc hai

Với A là một biểu thức đại số, ta gọi $\sqrt{A}$ là căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn hoặc biểu thức dưới dấu căn.

Ví dụ: $\sqrt{2x-1}$, $\sqrt{-\frac{1}{3}x+2}$ là các căn thức bậc hai.

Chú ý:

- Ta cũng nói $\sqrt{A}$ là một biểu thức. Biểu thức $\sqrt{A}$ xác định (hay có nghĩa) khi A nhận giá trị không âm.

- Khi A nhận giá trị không âm nào đó, khai phương giá trị này ta nhận được giá trị tương ứng của biểu thức $\sqrt{A}$.

Ví dụ:

+ Căn thức $\sqrt{2x+1}$ xác định khi $2x+1\ge 0$ hay $x\ge -\frac{1}{2}$.

Tại $x=4$ thì $\sqrt{2.4+1}=\sqrt{9}=\sqrt{3^2}=3$.

+ Giá trị của biểu thức $\sqrt{b^2-4ac}$ tại $a=3;b=10;c=3$ là:

$\sqrt{{10}^2-\mathrm{4.3.3}}=\sqrt{100-36}=\sqrt{64}=\sqrt{8^2}=8$.