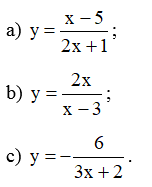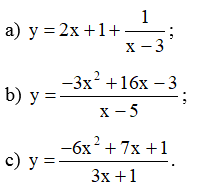Sách bài tập Toán 12 Bài 3 (Chân trời sáng tạo): Đường tiệm cận của đồ thị hàm số
Với giải sách bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 12 Bài 3.
Giải SBT Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Chân trời sáng tạo
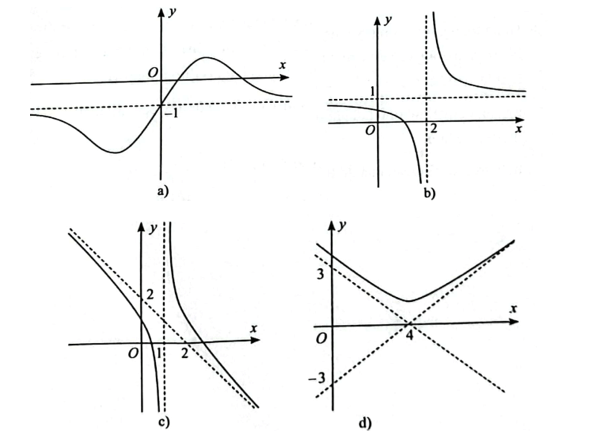
Bài 1 trang 21 SBT Toán 12 Tập 1: Tìm các đường tiệm cận của đồ thị hàm số sau:
Lời giải:
a) Quan sát đồ thị hàm số, ta thấy đồ thị hàm số có đường tiệm cận ngang y = −1.
b) Quan sát đồ thị hàm số, ta thấy đồ thị hàm số có đường tiệm cận ngang y = 1 và tiệm cận đứng x = 2.
c) Quan sát đồ thị hàm số, ta thấy đồ thị hàm số có đường tiệm cận đứng x = 1 và tiệm cận xiên là đường thẳng y = ax + b đi qua hai điểm (0; 2) và (2; 0).
Giải hệ phương trình {0.a+b=22a+b=0⇒{b=2a=−1.
Vậy đường tiệm cận xiên của đồ thị hàm số là y = −x + 2.
d) Quan sát đồ thị hàm số, ta thấy đồ thị hàm số có hai đường tiệm cận xiên.
Đường tiệm cận xiên thứ nhất y = a1x + b1 đi qua hai điểm có tọa độ (0; −3) và (4; 0).
Giải hệ phương trình, ta được: {a1.0+b1=−3a1.4+b1=0⇒{a1=34b1=−3.
Do đó, đường tiệm cận xiên thứ nhất là y = 34x−3.
Đường tiệm cận xiên thứ hai y = a2x + b2 đi qua hai điểm có tọa độ (0; 3) và (4; 0).
Giải hệ phương trình, ta được: {a2.0+b2=3a2.4+b2=0⇒{a1=−34b1=3.
Do đó, đường tiệm cận xiên thứ hai là: y = −34x+3.
Bài 2 trang 22 SBT Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
Lời giải:
a) Ta có: limx→−12+y=limx→−12+x−52x+1=−∞; limx→−12−y=limx→−12−x−52x+1=+∞.
Do đó, đường thẳng x = −12 là tiệm cận đứng của đồ thị hàm số.
limx→−∞y=limx→−∞x−52x+1=12; limx→+∞y=limx→+∞x−52x+1=12.
Do đó, đường thẳng y = 12 là tiệm ngang của đồ thị hàm số.
b) Ta có: limx→3+y=limx→3+2xx−3=+∞; limx→3−y=limx→3−2xx−3=−∞.
Do đó, đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.
limx→+∞y=limx→+∞2xx−3=2; limx→−∞y=limx→−∞2xx−3=2.
Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
c) Ta có: limx→−23+y=limx→−23+(−63x+2)=−∞; limx→−23−y=limx→−23−(−63x+2)=+∞.
Do đó, đường thẳng x = −23 là đường tiệm cận đứng của đồ thị hàm số.
limx→−∞y=limx→−∞(−63x+2)=0; limx→+∞y=limx→+∞(−63x+2)=0.
Do đó, đường thẳng y = 0 là đường tiệm cận ngang của đồ thị hàm số.
Bài 3 trang 22 SBT Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
Lời giải:
a) y=2x+1+1x−3
Ta có: limx→3+y=limx→3+(2x+1+1x−3)=+∞; limx→3−y=limx→3−(2x+1+1x−3)=−∞.
Do đó, đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.
limx→±∞[y−(2x+1)]=limx→±∞1x−3=0.
Do đó, đường thẳng y = 2x + 1laf tiệm cận xiên của đồ thị hàm số.
b) Ta có: y=−3x2+16x−3x−5 = −3x + 1 + 2x−5.
limx→5+y=limx→5+(−3x+1+2x−5)=+∞; limx→5−y=limx→5−(−3x+1+2x−5)=−∞.
Do đó, đường thẳng x = 5 là tiệm cận đứng của đồ thị hàm số.
limx→±∞[y−(−3x+1)]=limx→±∞2x−5=0.
Do đó, đường thẳng y = −3x + 1 là tiệm cận xiên của đồ thị hàm số.
c) Ta có: y=−6x2+7x+13x+1 = −2x + 3 – 23x+1
limx→−13+y=limx→−13+(−2x+3−23x+1)=+∞; limx→−13−y=limx→−13−(−2x+3−23x+1)=−∞.
Do đó, đường thẳng x = −13 là tiệm cận đứng của đồ thị hàm số.
limx→±∞[y−(−2x+3)]=limx→±∞−23x+1=0.
Do đó, đường thẳng y = −2x + 3 là tiệm cận xiên của đồ thị hàm số.
Bài 4 trang 22 SBT Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
a) y=x2+2x2+2x−3;
b) y = √x2−16.
Lời giải:
a) Ta có: limx→1+y=limx→1+x2+2x2+2x−3=+∞; limx→1−y=limx→1−x2+2x2+2x−3=−∞.
Do đó, đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số.
limx→−3+y=limx→−3+x2+2x2+2x−3=−∞; limx→−3−y=limx→−3−x2+2x2+2x−3=+∞.
Do đó, đường thẳng x = −3 là tiệm cận đứng của đồ thị hàm số.
limx→±∞y=limx→±∞x2+2x2+2x−3=1.
Do đó, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
b) Ta có: limx→−∞[y−(−x)]=limx→−∞[√x2−16+x]=0.
Do đó, đường thẳng y = −x là đường tiệm cận xiên của đồ thị hàm số.
limx→+∞[y−x]=limx→+∞[√x2−16−x]=0.
Do đó, đường thẳng y = x là đường tiệm cận xiên của đồ thị hàm số.
Bài 4 trang 22 SBT Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
a) y=x2+2x2+2x−3;
b) y = √x2−16.
Lời giải:
a) Ta có: limx→1+y=limx→1+x2+2x2+2x−3=+∞; limx→1−y=limx→1−x2+2x2+2x−3=−∞.
Do đó, đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số.
limx→−3+y=limx→−3+x2+2x2+2x−3=−∞; limx→−3−y=limx→−3−x2+2x2+2x−3=+∞.
Do đó, đường thẳng x = −3 là tiệm cận đứng của đồ thị hàm số.
limx→±∞y=limx→±∞x2+2x2+2x−3=1.
Do đó, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
b) Ta có: limx→−∞[y−(−x)]=limx→−∞[√x2−16+x]=0.
Do đó, đường thẳng y = −x là đường tiệm cận xiên của đồ thị hàm số.
limx→+∞[y−x]=limx→+∞[√x2−16−x]=0.
Do đó, đường thẳng y = x là đường tiệm cận xiên của đồ thị hàm số.
Bài 5 trang 22 SBT Toán 12 Tập 1: Chi phí để làm sạch p% lượng dầu loang từ một sự cố trên biển có thể được xấp xỉ bởi công thức
C(p) = 2000p100−p (tỉ đồng).
a) Tính chi phí để làm sạch 95%, 96%, 97%, 98% và 99% lượng dầu loang.
b) Tìm các tiệm cận của đồ thị hàm số C(p).
Lời giải:
a) Ta có: C(95) = 2000.95100−95=38000 tỉ đồng.
C(96) = 2000.96100−96=48000 tỉ đồng.
C(97) = 2000.97100−97=1940003 tỉ đồng.
C(98) = 2000.98100−98=96000 tỉ đồng.
C(99) = 2000.99100−99=198000 tỉ đồng.
b) Ta có: C(p) = 2000p100−p
limp→100+C(p)=limp→100+2000p100−p=+∞; limp→100−C(p)=limp→100−2000p100−p=−∞.
Do đó, đồ thị hàm số có đường tiệm cận đứng p = 100.
Bài 6 trang 22 SBT Toán 12 Tập 1: Hằng tháng, một công ty chuyên sản xuất mặt hàng A phải trả chi phí cố định là 50 triệu đồng (để thuê mặt bằng và lương nhân viên) và chi phí cho nguyên liệu là 10 000x (đồng) với x là số lượng sản phẩm A được nhập về.
a) Viết công thức tính chi phí trung bình ˉC(x) mà công ty cần chi phí để sản xuất một sản phẩm.
b) Tìm các tiệm cận của đồ thị hàm số ˉC(x)
Lời giải:
a) Ta có: ˉC(x)=50000000+10000xx=50000000x+10000.
b) Ta có:
limx→0+y=limx→0+(50000000x+10000)=+∞; limx→0−y=limx→0−(50000000x+10000)=−∞.
Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số.
limx→+∞y=limx→+∞(50000000x+10000)=10000; limx→−∞y=limx→−∞(50000000x+10000)=10000
Do đó, đường thẳng y = 10 000 là tiệm cận ngang của đồ thị hàm số.
Xem thêm các chương trình khác:
- Soạn văn 12 Chân trời sáng tạo (hay nhất)
- Văn mẫu 12 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 12 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn 12 - Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 12 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn 12 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 12 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh lớp 12 Friends Global đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh lớp 12 Friends Global đầy đủ nhất
- Giải sbt Tiếng Anh 12 – Friends Global
- Giải sgk Lịch sử 12 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 12 – Chân trời sáng tạo
- Giải sbt Lịch sử 12 – Chân trời sáng tạo
- Giải sgk Địa lí 12 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 12 – Chân trời sáng tạo
- Giải sbt Địa lí 12 – Chân trời sáng tạo
- Giải sgk Tin học 12 – Chân trời sáng tạo
- Giải Chuyên đề học tập Tin học 12 – Chân trời sáng tạo
- Giải sbt Tin học 12 – Chân trời sáng tạo
- Lý thuyết Tin học 12 - Chân trời sáng tạo
- Giải sgk Công nghệ 12 – Chân trời sáng tạo
- Giải sgk Kinh tế pháp luật 12 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 12 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 12 – Chân trời sáng tạo
- Giải sgk Giáo dục quốc phòng 12 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 12 – Chân trời sáng tạo
- Giải sgk Vật lí 12 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 12 – Chân trời sáng tạo
- Lý thuyết Vật lí 12 – Chân trời sáng tạo
- Giải sbt Vật lí 12 – Chân trời sáng tạo
- Giải sgk Hóa học 12 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa 12 – Chân trời sáng tạo
- Lý thuyết Hóa 12 – Chân trời sáng tạo
- Giải sbt Hóa 12 – Chân trời sáng tạo
- Giải sgk Sinh học 12 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 12 – Chân trời sáng tạo
- Lý thuyết Sinh học 12 – Chân trời sáng tạo
- Giải sbt Sinh học 12 – Chân trời sáng tạo