Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 12 Bài 3 (Chân trời sáng tạo): Biểu thức toạ độ của các phép toán vectơ

    Với giải sách bài tập Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 12 Bài 3.

    1 149 24/09/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ - Chân trời sáng tạo

    Bài 1 trang 76 SBT Toán 12 Tập 1: Tìm tọa độ ba vectơ a→,b→,c→ thỏa mãn a→=2i→+3j→−5k→, b→=−3j→+4k→, c→=−i→−2j→.

    Lời giải:

    Ta có: a→=2i→+3j→−5k→ suy ra a→ = (2; 3; −5).

    b→=−3j→+4k→ suy ra b→ = (0; −3; 4).

    c→=−i→−2j→ suy ra c→ = (−1; −2; 0).

    Bài 2 trang 76 SBT Toán 12 Tập 1: Cho hình bình hành OABD có OA→ = (−1; 1; 0) và OB→ = (1; 1; 0) với O là gốc tọa độ. Tìm tọa độ của điểm D.

    Lời giải:

    Do OABD là hình bình hành với O là gốc tọa độ, nên

    OD→=AB→=OB→−OA→=i→+j→−−i→+j→=2i→

    Suy ra OD→ = (2; 0; 0) hay D(2; 0; 0).

    Bài 3 trang 76 SBT Toán 12 Tập 1: Cho hình tứ diện OABC có G(3; −3; 6) là trọng tâm. Tìm tọa độ điểm A thỏa mãn AB→ = (1; 2; 3) và AC→ = (−1; 4; −2).

    Lời giải:

    Gọi A(a; b; c).

    Có G là trọng tâm nên GA→+GB→+GC→+GO→=0→

    ⇔GA→+GA→+AB→+GA→+AC→+GA→+AO→=0→

    ⇔ AB→+AC→+AO→=4AG→

    Ta có: AB→ = (1; 2; 3), AC→ = (−1; 4; −2), AO→ = (−a; −b; −c),

    ⇒ AB→+AC→+AO→ = (−a; 6 – b; 1 – c).

    AG→ = (3 – a; −3 – b; 6 – c) ⇒ 4AG→ = (12 – 4a; −12 – 4b; 24 – 4c).

    Do đó, −a=12−4a6−b=−12−4a1−c=24−4c⇒a=4b=−6c=233⇒ A4;−6;233

    Bài 4 trang 76 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' có A(2; 4; 0), B(4; 0; 0), C(−1; 4; −7) và D'(6; 8; 10). Tìm tọa độ của điểm B'.

    Lời giải:

    Do ABCD.A'B'C'D' là hình hộp nên ta có AB→=DC→=(2;−4;0).

    Gọi D(x; y; z) suy ra −1−x=24−y=−4−7−z=0⇒x=−3y=8z=−7 ⇒ D(−3; 8; −7).

    Ta có: BB'→=DD'→=9;0;17

    Gọi B'(a; b; c) suy ra a−4=9b−0=0c−0=17⇒a=13b=0c=17 ⇒ B'(13; 0; 17).

    Bài 5 trang 76 SBT Toán 12 Tập 1: Cho điểm A(2; 2; 1). Tính độ dài đoạn thẳng OA.

    Lời giải:

    Ta có: A(2; 2; 1), suy ra OA = OA→ = 22+22+12 = 3.

    Vậy OA = 3.

    Bài 6 trang 76 SBT Toán 12 Tập 1: Cho điểm A(1; 2; 3). Tính khoảng cách từ A đến trục Oy.

    Lời giải:

    Hình chiếu của A(1; 2; 3) trên trục Oy là A'(0; 2; 0).

    Khoảng cách từ A trên trục Oy là AA' = 1−02+2−22+3−02 = 10

    Bài 7 trang 76 SBT Toán 12 Tập 1: Cho điểm M(3; −1; 2). Tìm:

    a) Tọa độ điểm M' là điểm đối xứng của điểm M qua gốc tọa độ O.

    b) Tọa độ điểm O' là điểm đối xứng của điểm O qua điểm M.

    c) Khoảng cách từ M đến gốc tọa độ.

    d) Khoảng cách từ M đến mặt phẳng (Oxz).

    Lời giải:

    a) Tọa độ điểm M' là điểm đối xứng của điểm M qua gốc tọa độ O là M'(−3; 1; −2).

    b) O' là điểm đối xứng của điểm O qua điểm M suy ra M là trung điểm của OO'.

    Gọi O'(x; y; z) nên

    x+02=3y+02=−1z+02=2 ⇒ O'(6; −2; 4).

    c) Khoảng cách từ M đến gốc tọa độ là MO = 3−02+−1−02+2−02 = 14.

    d) Mặt phẳng (Oxz) là y = 0.

    Khoảng cách từ M đến mặt phẳng (Oxz) là d(M, (Oxz)) = 3.0+1.−1+2.002+12+02 = 1.

    Bài 8 trang 76 SBT Toán 12 Tập 1: Cho ba điểm A(0; 2; −1), B(−5; 4; 2), C(−1; 0; 5). Tìm tọa độ trọng tâm G của tam giác ABC.

    Lời giải:

    Gọi G(x; y; z) là trọng tâm tam giác ABC.

    Ta có:

    x=0+−5+−13=−2y=2+4+03=2z=−1+2+53=2⇒ G(−2; 2; 2).

    Vậy G(−2; 2; 2).

    Bài 9 trang 76 SBT Toán 12 Tập 1: Cho điểm M(a; b; c). Gọi A, B, C theo thứ tự là điểm đối xứng của điểm M qua các mặt phẳng (Oxy), (Oyz), (Oxz). Tìm tọa độ trọng tâm tam giác ABC.

    Lời giải:

    Ta có A đối xứng với M qua mặt phẳng (Oxy) nên A(a; b; −c).

    B đối xứng với M qua mặt phẳng (Oyz) nên B(−a; b; c).

    C đối xứng với M qua mặt phẳng (Oxz) nên C(a; −b; c).

    Gọi G(x; y; z) là trọng tâm tam giác ABC.

    Do đó,

    x=a+−a+a3=a3y=b+b+−b3=b3z=−c+c+c3=c3 ⇒ Ga3;b3;c3.

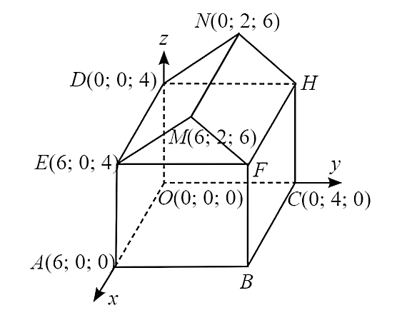
    Bài 10 trang 76 SBT Toán 12 Tập 1: Một nhân viên đang sử dụng phần mềm để thiết kế khung của một ngôi nhà trong không gian Oxyz được minh họa như Hình 3. Cho biết OABC.DEFH là hình hộp chữ nhật và EMF.DNH là hình lăng trụ đứng.

    Một nhân viên đang sử dụng phần mềm để thiết kế khung của một ngôi nhà

    a) Tìm tọa độ các điểm B, F, H.

    b) Tìm tọa độ các vectơ ME→,MF→.

    c) Tính số đo EMF^.

    Lời giải:

    a) Ta có OABC là hình chữ nhật nên OA→=CB→=6;0;0 ⇒ B(6; 4; 0).

    AEFB là hình chứ nhật nên AE→=BF→=0;0;4 ⇒ F(6; 4; 4).

    DEFH là hình chữ nhật nên ED→=FH→=6;0;0 ⇒ H(12; 4; 4).

    b) Ta có: ME→ = (0; −2; −2); MF→ = (0; 2; −2).

    c) Ta có: cosEMF^ = ME→.MF→ME→.MF→=0.0+−2.2+−2.−202+−22+−22.02+22+−22=0.

    ⇒ EMF^ = 90°.

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 149 24/09/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: