Sách bài tập Toán 12 Bài 4 (Chân trời sáng tạo): Khảo sát và vẽ đồ thị một số hàm số cơ bản

Giải SBT Toán 12 Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản - Chân trời sáng tạo

Bài 1 trang 31 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau:

a) y = x(x² – 4x);

b) y = −x³ + 3x² – 2.

Lời giải:

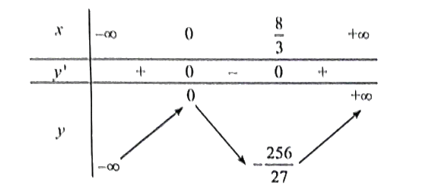
a) y = x(x² – 4x) = x³ – 4x²

Tập xác định: D = ℝ.

Ta có: y' = 3x² – 8x

y' = 0 ⇔ x = 0 hoặc x = $\frac{8}{3}$.

Ta có bảng biến thiên:

Hàm số đồng biến trên các khoảng (−∞; 0) và $\left(\frac{8}{3};+\infty \right)$.

Hàm số nghịch biến trên khoảng $\left(0;\frac{8}{3}\right)$.

Hàm số đạt cực đại tại x = 0, y_CĐ = 0.

Hàm số đạt cực tiểu tại x = $\frac{8}{3}$, y_CT = $-\frac{256}{27}$.

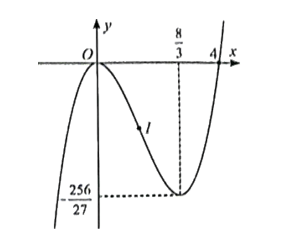
Đồ thị hàm số:

b) y = −x³ + 3x² – 2

Tập xác định: D = ℝ.

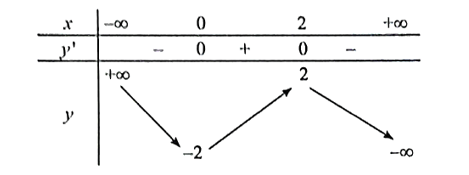
Ta có: y' = −3x² + 6x

y' = 0 ⇔ x = 0 hoặc x = 2.

Ta có bảng biến thiên:

Hàm số đồng biến trên khoảng (0; 2).

Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).

Hàm số đạt cực đại tại x = 2, y_CĐ = 2.

Hàm số đạt cực tiểu tại x = 0, y_CT = −2.

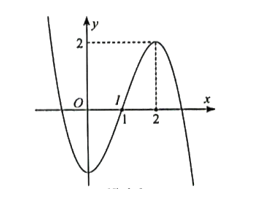
Đồ thị hàm số:

Bài 2 trang 31 SBT Toán 12 Tập 1: Cho hàm số y = (m – 1)x³ + 2(m + 1)x² – x + m – 1 (m là tham số)

a) Khảo sát và vẽ đồ thị của hàm số khi m = −1.

b) Tìm giá trị của m để tâm đối xứng của đồ thị hàm số có hoành độ x₀ = −2.

Lời giải:

a) Khi m = −1 ta được: y = −2x³ – x – 2.

Tập xác định: D = ℝ.

Ta có: y' = −6x² – 1

y' = 0 phương trình vô nghiệm.

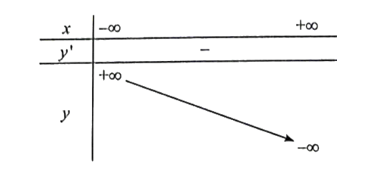
Ta có bảng biến thiên:

Hàm số nghịch biến trên ℝ.

Hàm số không cực trị.

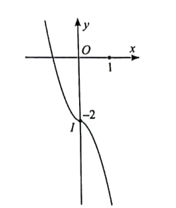
Đồ thị hàm số

b) Ta có: y = (m – 1)x³ + 2(m + 1)x² – x + m – 1

y' = 3(m – 1)x² + 4(m + 1)x – 1

y'' = 6(m – 1)x + 4(m + 1).

y'' = 0 ⇔ $\left\{\begin{array}{l}m-1\ne 0\\ x=\frac{-2\left(m+1\right)}{3\left(m-1\right)}\end{array}\right.$.

Để tâm đối xứng của đồ thị hàm số có hoành độ x₀ = −2.

⇔ $\left\{\begin{array}{l}m-1\ne 0\\ \frac{-2\left(m+1\right)}{3\left(m-1\right)}=-2\end{array}\right.$ ⇔ $\left\{\begin{array}{l}m\ne 1\\ 2m+2=6m-6\end{array}\right.$ ⇔ m = 2.

Bài 3 trang 31 SBT Toán 12 Tập 1: Cho hàm số y = 2x³ + 6x² – x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó.

Lời giải:

Ta có: y = 2x³ + 6x² – x + 2

y' = 6x² + 12x – 1

y'' = 12x + 12

y'' = 0 ⇔ x = −1.

Tâm đối xứng I của đồ thị hàm số có tọa độ I(−1; 7).

Với y'(−1) = −7, ta có phương trình tiếp tuyến tại I:

y = −7(x + 1) + 7 hay y = −7x.

Bài 4 trang 31 SBT Toán 12 Tập 1: Với giá trị nào của m thì đồ thị của hàm số y = −x³ – 3x² + mx + 1 có tâm đối xứng nằm trên trục Ox? Khi đó, có thể kết luận gì về số giao điểm của đồ thị hàm số với trục hoành?

Lời giải:

Ta có: y = −x³ – 3x² + mx + 1

y' = −3x² – 6x + m

y'' = −6x – 6;

y'' = 0 ⇔ x = −1.

Tâm đối xứng I của đồ thị hàm số có tung độ y_I = −m – 1.

I nằm trên trục Ox nên y_I = 0 ⇔ = −m – 1 = 0 ⇔ m = −1.

Khi m = −1, hàm số trở thành y = −x³ – 3x² − x + 1 và y' = −3x² – 6x – 1.

Phương trình y' = 0 có ∆ . 0 nên có hai nghiệm phân biệt, suy ra đồ thị hàm số có hai cực trị đối xứng qua I(−1; 0), nghĩa là tung độ của hai cực trị trái dấu nhau nên đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt.

Bài 5 trang 31 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau:

a) y = 3 + $\frac{1}{x}$;

b) y = 2 – $\frac{1}{1+x}$.

Lời giải:

a) y = 3 + $\frac{1}{x}$

Tập xác định: D = ℝ\{0}.

Giới hạn của hàm số:

$\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\left(3+\frac{1}{x}\right)=3$; $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\left(3+\frac{1}{x}\right)=3$.

Do đó, đồ thị hàm số có tiệm cận ngang y = 3.

$\underset{x\to 0^{+}}{\lim }y=\underset{x\to 0^{+}}{\lim }\left(3+\frac{1}{x}\right)=+\infty$; $\underset{x\to 0^{-}}{\lim }y=\underset{x\to 0^{-}}{\lim }\left(3+\frac{1}{x}\right)=-\infty$.

Do đó, đồ thị hàm số có tiệm cận đứng x = 0.

Ta có: y' = $-\frac{1}{x^2}$

y' < 0 với mọi x ≠ 0 nên hàm số nghịch biến trên các khoảng (−∞; 0) và (0; +∞).

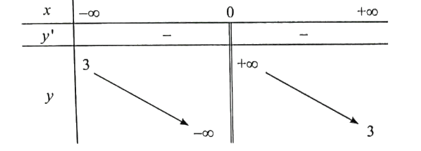
Ta có bảng biến thiên:

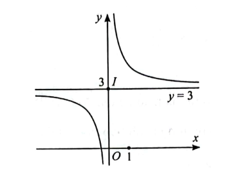
Đồ thị hàm số:

b) y = 2 – $\frac{1}{1+x}$

Tập xác định: D = ℝ\{−1}.

Giới hạn của hàm số:

$\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\left(2-\frac{1}{1+x}\right)=2$; $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\left(2-\frac{1}{1+x}\right)=2$.

Do đó, đồ thị hàm số có tiệm cận ngang y = 2.

$\underset{x\to -1^{+}}{\lim }y=\underset{x\to -1^{+}}{\lim }\left(2-\frac{1}{1+x}\right)=-\infty$; $\underset{x\to -1^{-}}{\lim }y=\underset{x\to -1^{-}}{\lim }\left(2-\frac{1}{1+x}\right)=+\infty$.

Do đó, đồ thị hàm số có tiệm cận đứng x = −1.

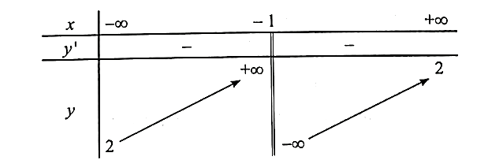
Ta có bảng biến thiên:

Ta có: y' = $\frac{1}{{\left(1+x\right)}^2}$ > 0 với mọi x ≠ −1 nên hàm số đồng biến trên khoảng (−∞; −1) và (−1; +∞).

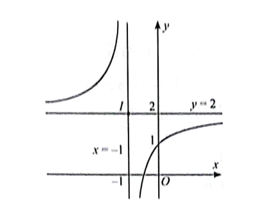
Đồ thị hàm số:

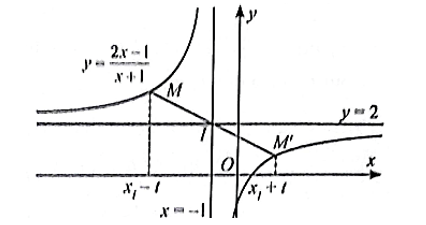
Bài 6 trang 32 SBT Toán 12 Tập 1: Ta đã biết đồ thị hàm số y = $\frac{2x-1}{x+1}$ có tiệm cận đứng là đường thẳng x = −1 và tiệm cận ngang là đường thẳng y = 2.

a) Tìm tọa độ giao điểm I của đường tiệm cận.

b) Với t tùy ý (t ≠ 0), gọi M và M' lần lượt là hai điểm trên đồ thị hàm số có hoành độ lần lượt là x_M = x_I – t và x_M' = x_I + t. Tìm các tung độ y(x_M) và y(x_M'). Từ đó, chứng minh rằng hai điểm M và M' đối xứng với nhau qua I.

Lời giải:

a) Đồ thị hàm số có tiệm cận đứng là đường thẳng x = −1 và tiệm cận ngang là đường thẳng y = 2 nên giao điểm I có tọa độ I(−1; 2).

b) Ta có: x_M = x_I – t = −1 – t ⇒ y_M = $\frac{2x_M-1}{x_M+1}$ = $\frac{2\left(-1-t\right)-1}{\left(-1-t\right)+1}$

x_M' = x_I + t = −1 + t ⇒ y_M' = $\frac{2x_{M^{\text{'}}}-1}{x_{M^{\text{'}}}+1}$ = $\frac{2\left(-1+t\right)-1}{\left(-1+t\right)+1}$.

Do đó, y_M + y_M' = $\frac{2\left(-1-t\right)-1}{\left(-1-t\right)+1}$ + $\frac{2\left(-1+t\right)-1}{\left(-1+t\right)+1}$ = 4 = 2y_I.

Mà x_M + x_M' = (−1 – t) + (−1 + t) = −2 = 2x_I.

Vậy I là trung điểm của MM' hay M và M' đối xứng với nhau qua I.

Bài 7 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{2x-1}{-x+3}$. Chứng tỏ rằng đường thẳng y = −x cắt đồ thị hàm số đã cho tại hai điểm phân biệt.

Lời giải:

Cách 1:

Xét phương trình hoành độ giao điểm, có: $\frac{2x-1}{-x+3}$ = −x (x ≠ 3).

⇔ 2x – 1 = −x(−x + 3)

⇔ 2x – 1 = x² – 3x

⇔ x² – 5x + 1 = 0

⇔ $\left\{\begin{array}{l}{3}^2-5.3+1=-5\ne 0\\ \Delta = {(-5)}^2-4.1=21>0\end{array}\right.$

Vậy phương trình có hai nghiệm phân biệt khác 3.

Vậy đường thẳng y = −x cắt đồ thị hàm số đã cho tại hai điểm phân biệt.

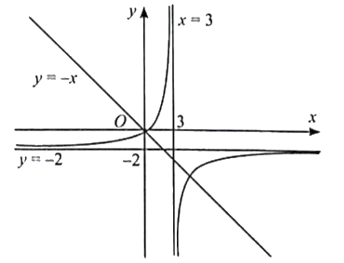
Cách 2:

Ta vẽ được đồ thị hàm số y = $\frac{2x-1}{-x+3}$ và đường thẳng y = −x trên cùng một hệ trục Oxy.

Ta thấy đường thẳng y = −x cắt đồ thị hàm số y = $\frac{2x-1}{-x+3}$ tại hai điểm phân biệt.

Bài 8 trang 32 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau:

a) $y=\frac{x^2-2x+2}{x-1}$;

b) $y=-2x+\frac{1}{2x+1}$.

Lời giải:

a) $y=\frac{x^2-2x+2}{x-1}$

Tập xác định: D = ℝ\{1}.

Giới hạn: $\underset{x\to +\infty }{\lim }y=+\infty$; $\underset{x\to -\infty }{\lim }y=-\infty$

$\underset{x\to +\infty }{\lim }\frac{y}{x}$ = 1 và $\underset{x\to +\infty }{\lim }(y-x)=-1$ nên đường thẳng y = x – 1 là tiệm cận xiên của đồ thị hàm số.

$\underset{x\to 1^{-}}{\lim }y=-\infty$ và $\underset{x\to 1^{+}}{\lim }y=+\infty$ nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

Ta có: y' = $\frac{x^2-2x}{{\left(x-1\right)}^2}$

y' = 0 ⇔ x = 0 hoặc x = 2.

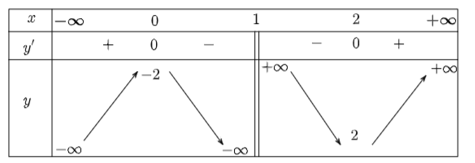
Ta có bảng biến thiên:

Hàm số đồng biến trên mỗi khoảng (−∞; 0) và (2; +∞).

Nghịch biến trên mỗi khoảng (0; 1) và (1; 2).

Hàm số đạt cực đại tại x = 0 và y_CĐ = −2.

Hàm số đạt cực tiểu tại x = 2 và y_CT = 2.

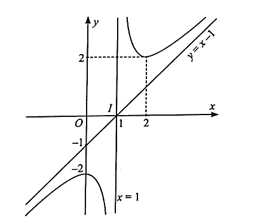
Đồ thị hàm số:

b) Tập xác định: D = ℝ\$\left\{-\frac{1}{2}\right\}$.

Ta có: $\underset{x\to +\infty }{\lim }y=-\infty$; $\underset{x\to -\infty }{\lim }y=+\infty$.

$\underset{x\to +\infty }{\lim }\frac{y}{x}$ = −2 và $\underset{x\to +\infty }{\lim }\left(y+2x\right)$ = 0 nên đường thẳng y = −2x là tiệm cận xiên của đồ thị hàm số.

$\underset{x\to {\frac{1}{2}}^{-}}{\lim }y=-\infty$ và $\underset{x\to {\frac{1}{2}}^{+}}{\lim }y=+\infty$ nên x = $-\frac{1}{2}$ là tiệm cận đứng của đồ thị hàm số.

Ta có: y' = $\frac{-2{\left(2x+1\right)}^2-2}{{\left(2x+1\right)}^2}$ = −2 – $\frac{2}{{\left(2x+1\right)}^2}$.

Vì y' < 0 với mọi x ≠ $-\frac{1}{2}$ nên hàm số nghịch biến trên mỗi khoảng $\left(-\infty ;-\frac{1}{2}\right)$ và $\left(-\frac{1}{2};+\infty \right)$.

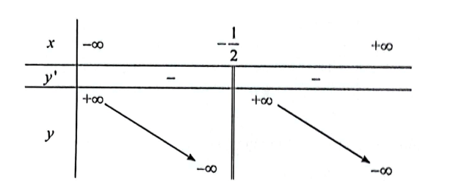
Bảng biến thiên:

Hàm số không có cực trị.

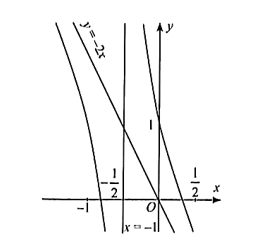
Đồ thị hàm số:

Bài 9 trang 32 SBT Toán 12 Tập 1: Cho hàm số $y=\frac{x^2+2x-2}{x-1}$

a) Tìm tọa độ giao điểm I của hai đường tiệm cận của đồ thị hàm số.

b) Với t tùy ý (t ≠ 0), gọi M và M' lần lượt là hai điểm trên đồ thị hàm số có hoành độ lần lượt là x_M = x_I – t và x_M' = x_I + t. so sánh các tung độ y_M và y_M'. Từ đó, suy ra rằng hai điểm M và M' đối xứng với nhau qua I.

Lời giải:

a) Ta có: $y=\frac{x^2+2x-2}{x-1}$ = x + 3 + $\frac{1}{x-1}$

$\underset{x\to 1^{+}}{\lim }y=+\infty$, $\underset{x\to 1^{-}}{\lim }y=-\infty$. Do đó, x = 1 là đường tiệm cận đứng của đồ thị hàm số.

$\underset{x\to +\infty }{\lim }\left[y-\left(x+3\right)\right]=\underset{x\to +\infty }{\lim }\frac{1}{x-1}=0$. Do đó, y = x + 3 là đường tiệm cận xiên của đồ thị hàm số.

Nhận thấy đồ thị hàm số có tiệm cận đứng x = 1 và tiệm cận ngang y = x + 3. Vậy giao điểm I có tọa độ I(1; 4).

b) Ta có: x_M = x_I – t = 1 – t; x_M' = x_I + t = 1 + t

y_M = $\frac{x_M^2+2x_M-2}{x_M-1}=\frac{{\left(1-t\right)}^2+2\left(1-t\right)-2}{\left(1-t\right)-1}$

y_M' = $\frac{x_{M^{\text{'}}}^2+2x_{M^{\text{'}}}-2}{x_{M^{\text{'}}}-1}=\frac{{\left(1+t\right)}^2+2\left(1+t\right)-2}{\left(1+t\right)-1}$

Do đó, y_M + y_M' = $\frac{{\left(1-t\right)}^2+2\left(1-t\right)-2}{\left(1-t\right)-1}$ + $\frac{{\left(1+t\right)}^2+2\left(1+t\right)-2}{\left(1+t\right)-1}$ = 8 = 2y_I.

Suy ra I là trung điểm của MM' hay M và M' đối xứng với nhau qua I.

Bài 10 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{\left(m-1\right)x-2}{m-2-x}$ (m là tham số).

Tìm điều kiện của m để đồ thị hàm số đã cho có một nhánh nằm hoàn toàn trong góc phần tư thứ nhất của hệ trục Oxy.

Lời giải:

Công thức hàm số có dạng y = $\frac{ax+b}{cx+d}$ với a = m – 1; b = −2; c = −1, d = m – 2.

Yêu cầu của bài toán được thỏa mãn khi và chỉ khi hàm số nghịch biến và có tiệm cận đứng không ở bên trái trục Oy, tiệm cận ngang không ở bên dưới trục Ox, nghĩa là:

$\left\{\begin{array}{l}ad-bc<0\\ c\ne 0\\ \frac{a}{c}\ge 0\\ -\frac{d}{c}\ge 0\end{array}\right.$ ⇔ $\left\{\begin{array}{l}\left(m-1\right)\left(m-2\right)-\left(-2\right)\left(-1\right)<0\\ -1\ne 0\\ \frac{m-1}{-1}\ge 0\\ \frac{m-2}{1}\ge 0\end{array}\right.$ ⇔ $\left\{\begin{array}{l}0<m<3\\ m\le 1\\ m\ge 2.\end{array}\right.$

Vậy không có giá trị m thỏa mãn yêu cầu.

Bài 11 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{x^2+2x-m}{x-1}$ (m là tham số).

a) Tìm m để đồ thị hàm số đã cho có hai điểm cực trị.

b) Chứng tỏ rằng khi m = 2, hàm số có hai điểm cực trị. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số này.

Lời giải:

a) y = $\frac{x^2+2x-m}{x-1}$

Tập xác định: D = ℝ\{1}.

Ta có: y' = $\frac{x^2-2x+m-2}{{\left(x-1\right)}^2}$

a) Đồ thị hàm số đã cho có hai cực trị khi và chỉ khi phương trình y' = 0 có hai nghiệm phân biệt.

⇔ x² – 2x + m – 2 = 0 có hai nghiệm phân biệt.

⇔ ∆' > 0 ⇔ 3 – m > 0 ⇔ m < 3.

Đồ thị hàm số đã cho có hai cực trị khi m < 3.

b) Nhận thấy m = 2 thỏa mãn điều kiện m < 3 nên khi đó hàm số có hai cực trị.

Với m = 2, ta có: y = $\frac{x^2+2x-2}{x-1}$ và y' = $\frac{x^2-2x}{{\left(x-1\right)}^2}$.

Phương trình y' = 0 ⇔ $\frac{x^2-2x}{{\left(x-1\right)}^2}$ = 0 ⇔ x = 0 hoặc x = 2.

Với x = 0 thì y = 2, với x = 2 thì y = 6.

Phương trình đường thẳng đi qua hai điểm cực trị có dạng y = ax + b.

Giải hệ phương trình, ta có: $\left\{\begin{array}{l}a.0+b=2\\ a.2+b=6\end{array}\right.\iff \left\{\begin{array}{l}a=2\\ b=2\end{array}\right.$.

Vậy y = 2x + 2.