Sách bài tập Toán 12 Bài 13 (Kết nối tri thức): Ứng dụng hình học của tích phân

Giải SBT Toán 12 Bài 13: Ứng dụng hình học của tích phân - Kết nối tri thức

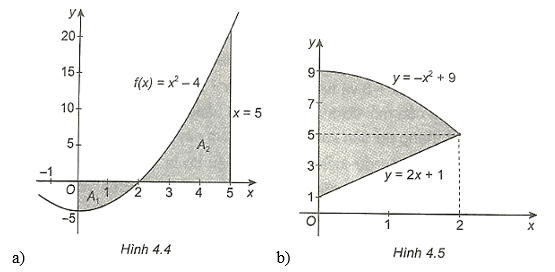
Bài 4.21 trang 17 SBT Toán 12 Tập 2: Tính diện tích của các hình phẳng được tô màu dưới đây:

Lời giải:

a) Diện tích cần tính là:

S = $\underset{0}{\overset{5}{\int }}\left|{\mathrm{x}}^2-4\right|\mathrm{d}\mathrm{x}=\underset{0}{\overset{2}{\int }}\left|{\mathrm{x}}^2-4\right|\mathrm{d}\mathrm{x}+\underset{2}{\overset{5}{\int }}\left|{\mathrm{x}}^2-4\right|\mathrm{d}\mathrm{x}$

= $\underset{0}{\overset{2}{\int }}\left(4-{\mathrm{x}}^2\right)\mathrm{d}\mathrm{x}+\underset{2}{\overset{5}{\int }}\left({\mathrm{x}}^2-4\right)\mathrm{d}\mathrm{x}$

= ${\left.\left(4\mathrm{x}-\frac{{\mathrm{x}}^3}{3}\right)\right|}_0^2+{\left.\left(\frac{{\mathrm{x}}^3}{3}-4\mathrm{x}\right)\right|}_2^5$

= 4.2 – $\frac{8}{3}$ − 4.0 + $\frac{0}{3}$ + $\frac{5^3}{3}$ − 4.5 – $\frac{8}{3}$ + 4.2 = $\frac{97}{3}$.

b) Diện tích cần tính là:

S = $\underset{0}{\overset{2}{\int }}\left|-{\mathrm{x}}^2+9-\left(2\mathrm{x}+1\right)\right|\mathrm{d}\mathrm{x}$ = $\underset{0}{\overset{2}{\int }}\left|-{\mathrm{x}}^2-2\mathrm{x}+8\right|\mathrm{d}\mathrm{x}$

= $\underset{0}{\overset{2}{\int }}\left(-{\mathrm{x}}^2-2\mathrm{x}+8\right)\mathrm{d}\mathrm{x}$

= ${\left.\left(\frac{-{\mathrm{x}}^3}{3}-{\mathrm{x}}^2+8\mathrm{x}\right)\right|}_0^2$ = $\frac{28}{3}$.

Bài 4.22 trang 17 SBT Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) y = (x – 1)³, y = x – 1,x = 0, x = 1.

b) y = x³ + 2x² – 3x, y = x² + 3x, x = −3, x = 0.

Lời giải:

a) Ta có: (x – 1)³ ≥ x – 1, với mọi x ∈ [0; 1].

Do đó, diện tích cần tính là:

S = $\underset{0}{\overset{1}{\int }}\left|{\left(x-1\right)}^3-\left(x-1\right)\right|dx$ = $\underset{0}{\overset{1}{\int }}\left[{\left(x-1\right)}^3-\left(x-1\right)\right]dx$

= $\underset{0}{\overset{1}{\int }}\left(x^3-3x^2+2x\right)dx$

= ${\left.\left(\frac{x^4}{4}-x^3+x^2\right)\right|}_0^1$ = $\frac{1}{4}$.

b) Ta có: x³ + 2x² – 3x – x² – 3x = x³ + x² – 6x = x(x – 2)(x + 3) ≥ 0, với mọi x ∈ [−3; 0].

Do đó, diện tích cần tính là:

S = $\underset{-3}{\overset{0}{\int }}\left|x^3+2x^2–3x–x^2–3x\right|dx$

= $\underset{-3}{\overset{0}{\int }}\left|x^3+x^2-6x\right|dx$

= $\underset{-3}{\overset{0}{\int }}\left(x^3+x^2-6x\right)dx$

= ${\left.\left(\frac{x^4}{4}+\frac{x^3}{3}-3x^2\right)\right|}_{-3}^0$

= $\frac{63}{4}$.

Bài 4.23 trang 17 SBT Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) y = e^x, y = $\sqrt{\mathrm{x}}$, x = 0, x = 1;

b) y = cosx, y = $\frac{1}{2}$, x = 0, x = $\frac{\mathrm{\pi }}{3}$.

Lời giải:

a) Ta có: e^x ≥ 1 ≥ $\sqrt{\mathrm{x}}$, với mọi x ∈ [0; 1], nên diện tích cần tính là:

S = $\underset{0}{\overset{1}{\int }}\left|{\mathrm{e}}^{\mathrm{x}}-\sqrt{\mathrm{x}}\right|\mathrm{d}\mathrm{x}=\underset{0}{\overset{1}{\int }}\left({\mathrm{e}}^{\mathrm{x}}-\sqrt{\mathrm{x}}\right)\mathrm{d}\mathrm{x}$ = ${\left.\left({\mathrm{e}}^{\mathrm{x}}-\frac{2}{3}{\mathrm{x}}^{\frac{3}{2}}\right)\right|}_0^1$ = e − $\frac{5}{3}$.

b) Vì cosx ≥ $\frac{1}{2}$, với mọi x ∈ $\left[0;\frac{\pi }{3}\right]$, nên diện tích cần tính là:

S = $\underset{0}{\overset{\frac{\pi }{3}}{\int }}\left|\cos x-\frac{1}{2}\right|dx=\underset{0}{\overset{\frac{\pi }{3}}{\int }}\left(\cos x-\frac{1}{2}\right)dx$

$=\left(\sin x-\frac{1}{2}\right){|}_0^{\frac{\pi }{3}}=\frac{\sqrt{3}}{2}-\frac{\pi }{6}$.

Bài 4.24 trang 17 SBT Toán 12 Tập 2: Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox:

a) y = $2\sqrt{\mathrm{x}}$, y = 0, x = 1, x = 4.

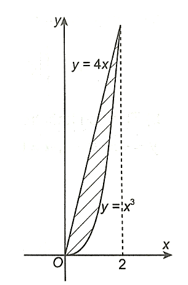
b) y = 4x, y = x³, x = 0, x = 2.

Lời giải:

a) Thể tích cần tính là:

V = π$\underset{1}{\overset{4}{\int }}{\left(2\sqrt{x}\right)}^{2}dx=\pi \underset{1}{\overset{4}{\int }}4xdx=\pi 2x^2{|}_1^4=30\pi$

b)

Đồ thị hàm số y = 4x nằm phía trên đồ thị hàm số y = x³ so với trục hoành, với mọi x ∈ [0; 2].

Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường thẳng y = 4x, y = 0, x = 0, x = 2 quanh trục Ox là:

V₁ = $\mathrm{\pi }\underset{0}{\overset{2}{\int }}{\left(4\mathrm{x}\right)}^2\mathrm{d}\mathrm{x}=\mathrm{\pi }\underset{0}{\overset{2}{\int }}16{\mathrm{x}}^2\mathrm{d}\mathrm{x}=\frac{128\mathrm{\pi }}{3}$.

Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường y = x³, y = 0, x = 0, x = 2 quanh trục Ox là:

V₂ = $\mathrm{\pi }\underset{0}{\overset{2}{\int }}{\left({\mathrm{x}}^3\right)}^2\mathrm{d}\mathrm{x}=\mathrm{\pi }\underset{0}{\overset{2}{\int }}{\mathrm{x}}^6\mathrm{d}\mathrm{x}=\frac{128\mathrm{\pi }}{7}$.

Thể tích cần tính là: V = V₁ – V₂ = $\frac{128\mathrm{\pi }}{3}$ − $\frac{128\mathrm{\pi }}{7}$ = $\frac{512\mathrm{\pi }}{21}$.

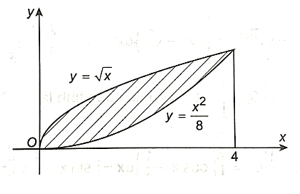
Bài 4.25 trang 17 SBT Toán 12 Tập 2: Xét hình phẳng giới hạn bởi các đường y = $\sqrt{\mathrm{x}}$, y = $\frac{{\mathrm{x}}^2}{8}$, x = 0, x = 4.

a) Tính diện tích hình phẳng.

b) Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng xung quanh trục Ox.

Lời giải:

a) Ta có đồ thị hàm số như sau:

Quan sát đồ thị, ta thấy đồ thị hàm số y = $\sqrt{\mathrm{x}}$ nằm phía trên đồ thị hàm số y = $\frac{{\mathrm{x}}^2}{8}$ so với trục hoành, với x ∈ [0; 4].

Diện tích cần tính là:

S = $\underset{0}{\overset{4}{\int }}\left|\sqrt{\mathrm{x}}-\frac{{\mathrm{x}}^2}{8}\right|\mathrm{d}\mathrm{x}=\underset{0}{\overset{4}{\int }}\left(\sqrt{\mathrm{x}}-\frac{{\mathrm{x}}^2}{8}\right)\mathrm{d}\mathrm{x}=\left(\frac{2}{3}\mathrm{x}\sqrt{\mathrm{x}}-\frac{{\mathrm{x}}^3}{24}\right){|}_0^4=\frac{8}{3}$.

b) Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường y = $\sqrt{\mathrm{x}}$, y = 0, x = 0, x = 4 quanh trục Ox là:

V₁ = $\mathrm{\pi }\underset{0}{\overset{4}{\int }}{\left(\sqrt{\mathrm{x}}\right)}^2\mathrm{d}\mathrm{x}=\mathrm{\pi }\underset{0}{\overset{4}{\int }}\mathrm{x}\mathrm{d}\mathrm{x}=\frac{\mathrm{\pi }{\mathrm{x}}^2}{2}{|}_0^4=8\mathrm{\pi }.$

Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường y = $\frac{{\mathrm{x}}^2}{8}$, y = 0, x = 0, x = 2 quanh trục Ox là:

V₂ = $\mathrm{\pi }\underset{0}{\overset{4}{\int }}{\left(\frac{{\mathrm{x}}^2}{8}\right)}^2\mathrm{d}\mathrm{x}=\mathrm{\pi }\underset{0}{\overset{4}{\int }}\frac{{\mathrm{x}}^4}{64}\mathrm{d}\mathrm{x}=\frac{\mathrm{\pi }{\mathrm{x}}^5}{320}{|}_0^4=\frac{16\mathrm{\pi }}{5}.$

Thể tích cần tính là:

V = V₁ – V₂ = $8\mathrm{\pi }-\frac{16\mathrm{\pi }}{5}=\frac{24\mathrm{\pi }}{5}$.

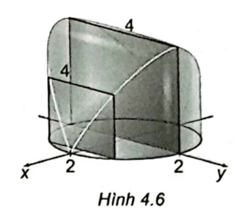
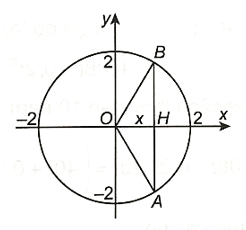
Bài 4.26 trang 18 SBT Toán 12 Tập 2: Tính thể tích của vật thể ℬ, biết đáy của ℬ là hình tròn bán kính 2 và mặt cắt vuông góc với mặt đáy là những hình vuông (H.4.6).

Lời giải:

Ta có hình sau:

Mỗi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (−2 ≤ x ≤ 2) cắt vật thể theo mặt cắt là hình vuông có độ dài cạnh là AB = 2BH = $2\sqrt{4-x^2}$.

Khi đó diện tích mặt cắt là 4(4 – x²).

Vậy thể tích của vật thể là: V = $\underset{-2}{\overset{2}{\int }}4\left(4-x^2\right)dx=\frac{128}{3}$.

Bài 4.27 trang 18 SBT Toán 12 Tập 2: Hàm cầu và hàm cung của một sản phẩm được mô hình hóa bởi:

Hàm cầu: p = −0,2x + 8 và hàm cung: p = 0,1x + 2, trong đó x là số đơn vị sản phẩm, p là giá của mỗi đơn vị sản phẩm (tính bằng triệu đồng). Tìm thặng dư tiêu dùng và thặng dư sản xuất đối với sản phẩm này.

Lời giải:

Xét phương trình −0,2x + 8 = 0,1x + 2 ⇔ x = 20, khi đó p = −0,2.20 + 8 = 4.

Thặng dư tiêu dùng là:

$\underset{0}{\overset{20}{\int }}\left(-0,2x+8-3\right)dx=\left(-0,1+4x\right){|}_0^{20}$ = 40 (triệu đồng).

Thặng dư sản xuất là:

$\underset{0}{\overset{20}{\int }}\left[4-\left(0,1x+2\right)\right]dx=\left(2x-0,1.\frac{x^2}{2}\right){|}_0^{20}$ = 20 (triệu đồng).

Bài 4.28 trang 18 SBT Toán 12 Tập 2: Chi phí nhiên liệu dự kiến C (tính bằng triệu đô la mỗi năm) khi sử dụng một loại xe tải của một công ty vận tải từ năm 2020 đến năm 2030 là C₁ = 5,6 + 2,2t, 0 ≤ t ≤ 10, trong đó t = 0 tương ứng với năm 2020. Nếu công ty sử dụng một loại xe tải khác có động cơ hiệu quả hơn thì chi phí nhiên liệu dự kiến sẽ giảm và tuân theo hàm mô hình C₂ = 4,7 + 2,04t, 0 ≤ t ≤ 10. Công ty có thể tiết kiệm được bao nhiêu khi sử dụng lạo xe tải với động cơ hiệu quả hơn?

Lời giải:

Tổng chi phí nhiên liệu khi công ty vận tải sử dụng xe tải loại thứ nhất trong 10 năm là:

S₁ = $\underset{0}{\overset{10}{\int }}{\mathrm{C}}_1\mathrm{d}\mathrm{t}=\underset{0}{\overset{10}{\int }}\left(5,6+2,2\mathrm{t}\right)\mathrm{d}\mathrm{t}=\left(5,6\mathrm{t}+1,1{\mathrm{t}}^2\right){|}_0^{10}$ = 166 (triệu đô la).

Tổng chi phí nhiên liệu khi công ty vận tải sử dụng xe tải loại thứ hai trong 10 năm là:

S₂ = $\underset{0}{\overset{10}{\int }}{\mathrm{C}}_2\mathrm{d}\mathrm{t}=\underset{0}{\overset{10}{\int }}\left(4,7+2,04\mathrm{t}\right)\mathrm{d}\mathrm{t}=\left(4,7\mathrm{t}+1,02{\mathrm{t}}^2\right){|}_0^{10}$ = 149 (triệu đô la).

Vậy khi sử dụng loại xe tải với động cơ hiệu quả hơn, công ty tiết kiệm được:

166 – 149 = 17 (triệu đô la).

Bài 4.29 trang 18 SBT Toán 12 Tập 2: Doanh thu từ một quy trình sản xuất (tính bằng triệu đô la mỗi năm) được dự kiến sẽ tuân theo mô hình R = 100 + 0,08t trong 10 năm. Trong cùng khoảng thời gian đó, chi phí (tính bằng triệu đô la mỗi năm) được dự kiến sẽ tăng theo mô hình C = 60 + 0,2t², trong đó t là thời gian (tính bằng năm). Ước tính lợi nhuận trong khoảng thời gian 10 năm.

Lời giải:

Hàm lợi nhuận là P = R – C = 40 + 0,08t – 0,2t².

Ước tính lợi nhuận trong khoảng thời gian 10 năm là: ≈ 337,33 (triệu đô la).

Bài 4.30 trang 18 SBT Toán 12 Tập 2: Một trận dịch lây lan đến mức sau khi bùng phát t tuần số người nhiễm bệnh là:

N₁(t) = 0,1t² + 0,5t + 150, 0 ≤ t ≤ 50.

Hai mươi lăm tuần sau dịch sẽ bùng phát, một loại vắc xin đã được phát triển và tiêm cho công chúng. Khi đó, số người nhiễm bệnh được điều chỉnh theo mô hình

N₂(t) = −0,2t² + 6t + 200, 25 ≤ t ≤ 50.

a) Thời điểm t để sau khi tiêm vắc xin thì dịch bệnh kết thúc, tức là số người nhiễm bệnh N₂(t) = 0.

b) Ước tính gần đúng số người mà vắc xin đã ngăn ngừa khỏi dịch bệnh trong thời gian xảy ra dịch bệnh.

Lời giải:

a) Thời gian t mà dịch bệnh kết thúc thỏa mãn phương trình:

−0,2t² + 6t + 200 = 0 ⇔ t = 50 (vì t ≥ 0).

b) Như vậy khi có vắc xin tiêm cho công chúng từ tuần thứ hai mươi lăm tới tuần thứ năm mươi khi kết thúc dịch (theo mô hình chỉ ra).

Số người mà vắc xin đã ngăn ngừa khỏi bệnh trong thời gian xảy ra dịch bệnh là:

$\underset{25}{\overset{50}{\int }}\left[{\mathrm{N}}_1\left(\mathrm{t}\right)-{\mathrm{N}}_2\left(\mathrm{t}\right)\right]\mathrm{d}\mathrm{t}=\underset{25}{\overset{50}{\int }}\left(0,3{\mathrm{t}}^2-5,5\mathrm{t}-50\right)\mathrm{d}\mathrm{t}$

= ${\left.\left(0,1{\mathrm{t}}^3-5,5.\frac{{\mathrm{t}}^2}{2}-50\mathrm{t}\right)\right|}_{25}^{50}$ ≈ 4 531

Xem thêm Lời giải bài tập Toán 12 sách Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 4

Bài 14: Phương trình mặt phẳng

Bài 15: Phương trình đường thẳng trong không gian

Bài 16: Công thức tính góc trong không gian

Bài 17: Phương trình mặt cầu