Sách bài tập Toán 12 (Kết nối tri thức): Bài tập cuối chương 4

Giải SBT Toán 12 Bài tập cuối chương 4 - Kết nối tri thức

Bài 4.31 trang 19 SBT Toán 12 Tập 2: $\int {\mathrm{x}}^2\mathrm{d}\mathrm{x}$ bằng:

A. 2x + C.

B. $\frac{1}{3}$x³ + C.

C. x³ + C.

D. 3x³ + C.

Lời giải:

Đáp án đúng là: B

Ta có: $\int {\mathrm{x}}^2\mathrm{d}\mathrm{x}$ = $\frac{1}{3}$x³ + C.

Bài 4.32 trang 19 SBT Toán 12 Tập 2: $\int \left({\mathrm{x}}^2+3{\mathrm{x}}^3\right)\mathrm{d}\mathrm{x}$ có dạng $\frac{\mathrm{a}}{3}$x³ + $\frac{\mathrm{b}}{4}$x⁴ + C, trong đó a, b là hai số nguyên. Giá trị a + b bằng:

A. 4.

B. 2.

C. 5.

D. 6.

Lời giải:

Đáp án đúng là: A

Ta có: $\int \left({\mathrm{x}}^2+3{\mathrm{x}}^3\right)\mathrm{d}\mathrm{x}$ = $\int {\mathrm{x}}^2\mathrm{d}\mathrm{x}+\int 3{\mathrm{x}}^3\mathrm{d}\mathrm{x}$ = $\frac{{\mathrm{x}}^3}{3}+\frac{3{\mathrm{x}}^4}{4}+\mathrm{C}$.

Vậy a = 1, b = 3.

Khi đó a + b = 4.

Bài 4.33 trang 19 SBT Toán 12 Tập 2: Cho $\underset{0}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}=3$ và $\underset{2}{\overset{5}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$ = 7. Giá trị của $\underset{0}{\overset{5}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$ là

A. 10.

B. 4.

C. −4.

D. 3.

Lời giải:

Đáp án đúng là: A

Ta có: $\underset{0}{\overset{5}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$ = $\underset{0}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}+\underset{2}{\overset{5}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$ = 3 + 7 = 10.

Bài 4.34 trang 19 SBT Toán 12 Tập 2: Cho hàm số f(x) liên tục trên ℝ và $\underset{0}{\overset{4}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}=4$. Giá trị của tích phân $\underset{0}{\overset{4}{\int }}2\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$ là

A. 2.

B. 4.

C. 8.

D. 16.

Lời giải:

Đáp án đúng là: C

Ta có: $\underset{0}{\overset{4}{\int }}2\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$ = $2\underset{0}{\overset{4}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$ = 2.4 = 8.

Bài 4.35 trang 19 SBT Toán 12 Tập 2: Cho hàm số f(x) có đạo hàm f'(x) liên tục trên ℝ, f(0) = 1 và $\underset{0}{\overset{2}{\int }}{\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}=4$. Khi đó giá trị f(2) bằng

A. 5.

B. −3.

C. 6.

D. 8.

Lời giải:

Đáp án đúng là: A

Ta có: $\underset{0}{\overset{2}{\int }}{\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}=4$ = ${\left.\mathrm{f}\left(\mathrm{x}\right)\right|}_0^2$⇔ f(2) – f(0) = 4 ⇔ f(2) = 5.

Bài 4.36 trang 19 SBT Toán 12 Tập 2: Giá trị trung bình của hàm f(x) trên đoạn [a; b] được tính bởi công thức m = $\frac{1}{\mathrm{b}-\mathrm{a}}\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$. Khi đó, giá trị trung bình của hàm số f(x) = x² + 2x trên đoạn [0; 3] là

A. $\frac{8}{3}$.

B. 18.

C. 6.

D. 5.

Lời giải:

Đáp án đúng là: C

Ta có: m = $\frac{1}{\mathrm{b}-\mathrm{a}}\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$.

Với f(x) = x² + 2x trên đoạn [0; 3], ta được

m = $\frac{1}{3-0}\underset{0}{\overset{3}{\int }}\left({\mathrm{x}}^2+2\mathrm{x}\right)\mathrm{d}\mathrm{x}$ = ${\left.\frac{1}{3}\left(\frac{{\mathrm{x}}^3}{3}+{\mathrm{x}}^2\right)\right|}_0^3$ = 6.

Vậy m = 6.

Bài 4.37 trang 20 SBT Toán 12 Tập 2: Cho hàm số y = f(x) liên tục trên [a; b] và f(x) ≤ 0, ∀x ∈ [a; b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b được tính bằng công thức

A. S = $\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$.

B. S = $-\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$.

C. S = $\mathrm{\pi }\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$.

D. S = $\mathrm{\pi }\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}{\left[\mathrm{f}\left(\mathrm{x}\right)\right]}^2\mathrm{d}\mathrm{x}$.

Lời giải:

Đáp án đúng là: B

Ta có công thức: S = $\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}=-\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$ (do f(x) ≤ 0, ∀x ∈ [a; b]).

Bài 4.38 trang 20 SBT Toán 12 Tập 2: Một đất nước tiêu thụ dầu theo tốc độ xác định bởi r(t) = 20.e^0,2t tỉ thùng mỗi năm, trong đó t là thời gian tính theo năm, 0 ≤ t ≤ 10. Trong khoảng 10 năm kể trên, nước đó đã tiêu thụ lượng dầu là

A. r(10).

B. r(10) – r(0).

C. $\underset{0}{\overset{10}{\int }}{\mathrm{r}}^{\text{'}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}$.

D. $\underset{0}{\overset{10}{\int }}\mathrm{r}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}$.

Lời giải:

Đáp án đúng là: D

Trong khoảng 10 năm kể trên, nước đó đã tiêu thụ lượng dầu là $\underset{0}{\overset{10}{\int }}\mathrm{r}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}$.

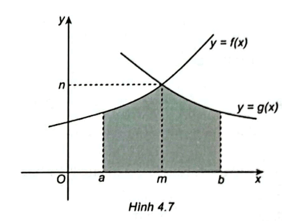
Bài 4.39 trang 20 SBT Toán 12 Tập 2: Cho S là diện tích phần hình phẳng được tô màu như Hình 4.7.

Khi đó biểu thức tính diện tích S là

A. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}$.

B. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{m}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}+\underset{\mathrm{m}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}$.

C. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{m}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}+\underset{\mathrm{m}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}$.

D. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{m}}{\int }}\left|\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}+\underset{\mathrm{m}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}$.

Lời giải:

Đáp án đúng là: C

Biểu thức tính diện tích S là $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{m}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}+\underset{\mathrm{m}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{d}\mathrm{x}$.

Bài 4.40 trang 21 SBT Toán 12 Tập 2: Khi nghiên cứu một quần thể vi khuẩn, người ta nhận thấy quần thể vi khuẩn đó ở ngày thứ t có số lượng N(t) con. Biết rằng tốc độ phát triển của quần thể đó là N'(t) = $\frac{8000}{\mathrm{t}}$ và sau ngày thứ nhất (t = 1) có 250 000 con. Sau 6 ngày (t = 6), số lượng của quần thể vi khuẩn là

A. 353 584 con.

B. 234 167 con.

C. 288 959 con.

D. 264 334 con.

Lời giải:

Đáp án đúng là: D

Ta có N(t) = $\int {\mathrm{N}}^{\text{'}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}=\int \frac{8000\mathrm{d}\mathrm{t}}{\mathrm{t}}=8000\int \frac{\mathrm{d}\mathrm{t}}{\mathrm{t}}$ = 8 000ln|t| + C.

Ngày thứ nhất, số lượng vi khuẩn là 250 000 con, nên N(1) = 250 000 con, tức là C = 250 000.

Số lượng vi khuẩn sau 6 ngày là:

N(6) = 8 000.ln|6| + 250 000 ≈ 264 334 (con).

Bài 4.41 trang 21 SBT Toán 12 Tập 2: Tìm họ tất cả các nguyên hàm của các hàm số sau:

a) $\mathrm{y}={\sin }^2\frac{\mathrm{x}}{2}$;

b) y = e^2x – 2x⁵ + 5.

Lời giải:

a) $\mathrm{y}={\sin }^2\frac{\mathrm{x}}{2}$ = $\frac{1-\cos \mathrm{x}}{2}$.

Ta có: $\int {\sin }^2\frac{\mathrm{x}}{2}\mathrm{d}\mathrm{x}=\int \frac{1-\cos \mathrm{x}}{2}\mathrm{d}\mathrm{x}=\frac{1}{2}\mathrm{x}-\frac{1}{2}\sin \mathrm{x}+\mathrm{C}$.

b) Ta có: $\int \left({\mathrm{e}}^{2\mathrm{x}}-2{\mathrm{x}}^5+5\right)\mathrm{d}\mathrm{x}$ = $\int {\mathrm{e}}^{2\mathrm{x}}\mathrm{d}\mathrm{x}-\int 2{\mathrm{x}}^5\mathrm{d}\mathrm{x}+\int 5\mathrm{d}\mathrm{x}$

= $\frac{1}{2}{\mathrm{e}}^{2\mathrm{x}}-\frac{1}{3}{\mathrm{x}}^6+5\mathrm{x}+\mathrm{C}$

Bài 4.42 trang 21 SBT Toán 12 Tập 2: Tìm một nguyên hàm F(x) của hàm số f(x) = 2x − $\frac{1}{x}$ thỏa mãn điều kiện F(1) = 3.

Lời giải:

Ta có: $\int f\left(x\right)dx=\int \left(2x-\frac{1}{x}\right)dx=x^2-\ln \left|x\right|+C$.

Mà F(1) = 3 ⇒ 1² – ln1 + C = 3 ⇔ C = 2.

Vậy F(x) = x² – ln|x| + 2.

Bài 4.43 trang 21 SBT Toán 12 Tập 2: Tính:

a) $\underset{0}{\overset{3}{\int }}\left|3-x\right|dx$;

b) $\underset{0}{\overset{2}{\int }}\left(e^x-4x^3\right)dx$;

c) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(\sin x+\cos x\right)dx$.

Lời giải:

a) $\underset{0}{\overset{3}{\int }}\left|3-x\right|dx$ = $\underset{0}{\overset{3}{\int }}\left(-x+3\right)dx$ = $\left(\frac{-x^2}{2}+3x\right){|}_0^3$

= $\frac{3^2}{2}+3.3-\frac{0^2}{2}-3.0$ = $\frac{9}{2}$.

b) $\underset{0}{\overset{2}{\int }}\left(e^x-4x^3\right)dx$ = $\left(e^x-x^4\right){|}_0^2$ = e² – 2⁴ – e⁰ + 0⁴ = e² – 17.

c) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(\sin x+\cos x\right)dx$ = $\left(-\cos x+\sin x\right){|}_0^{\frac{\pi }{2}}$ = 2.

Bài 4.44 trang 21 SBT Toán 12 Tập 2: Tính diện tích S của hình phẳng được giới hạn bởi đồ thị hàm số y = 3x² + 1, trục hoành và hai đường thẳng x = 0, x = 2.

Lời giải:

Diện tích hình phẳng hình phẳng được giới hạn bởi đồ thị hàm số y = 3x² + 1, trục hoành và hai đường thẳng x = 0, x = 2 là:

S = $\underset{0}{\overset{2}{\int }}\left|3{\mathrm{x}}^2+1\right|\mathrm{d}\mathrm{x}=\underset{0}{\overset{2}{\int }}\left(3{\mathrm{x}}^2+1\right)\mathrm{d}\mathrm{x}=\left({\mathrm{x}}^3+\mathrm{x}\right){|}_0^2$ = 10.

Vậy diện tích hình phẳng cần tính là S = 10.

Bài 4.45 trang 21 SBT Toán 12 Tập 2: Cho hình phẳng D giới hạn bởi đồ thị hàm số y = $\sqrt{{\mathrm{x}}^2+1}$, trục hoành và hai đường thẳng x = 0, x = 1. Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành.

Lời giải:

Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y = $\sqrt{{\mathrm{x}}^2+1}$, trục hoành và hai đường thẳng x = 0, x = 1 là:

V = $\mathrm{\pi }\underset{0}{\overset{1}{\int }}{\left(\sqrt{{\mathrm{x}}^2+1}\right)}^2\mathrm{d}\mathrm{x}$ = $\mathrm{\pi }\left(\frac{1}{3}{\mathrm{x}}^3+\mathrm{x}\right){|}_0^1$ = $\frac{4}{3}\mathrm{\pi }$.

Vậy thể tích khối tròn xoay là V = $\frac{4}{3}\mathrm{\pi }$.

Bài 4.46 trang 21 SBT Toán 12 Tập 2: Có bao nhiêu giá trị nguyên dương của tham số m để $\underset{0}{\overset{3}{\int }}\left(10x-2m\right)dx>0$?

Lời giải:

Ta có: $\underset{0}{\overset{3}{\int }}\left(10x-2m\right)dx$ = $\left(5x^2-2mx\right){|}_0^3$ = 5.3² – 6m = 45 – 6m.

Mà theo đề bài, $\underset{0}{\overset{3}{\int }}\left(10x-2m\right)dx>0$ ⇔ 45 – 6m > 0 ⇔ m < $\frac{45}{6}$= 7,5.

Lại có m nhận giá trị nguyên dương, nên m ∈ {1; 2; 3; 4; 5; 6; 7}.

Có 7 giá trị nguyên dương m thỏa mãn yêu cầu bài toán.

Bài 4.47 trang 21 SBT Toán 12 Tập 2: Khi nghiên cứu dịch sốt xuất huyết ở một địa phương, các chuyên gia y tế ước tính rằng tại ngày thứ m có F(m) người mắc bệnh (sau khi đã làm tròn đến chữ số hàng đơn vị). Biết rằng tốc độ lan truyền bệnh là F'(m) = $\frac{150}{2\mathrm{m}+1}$ và ngày đầu tiên (m = 0) người ta phát hiện ra 50 bệnh nhân. Hãy xác định biểu thức của F(m) và số người mắc bệnh ở ngày thứ 10.

Lời giải:

Từ giả thiết, ta có:

F(m) = $\int {\mathrm{F}}^{\text{'}}\left(\mathrm{m}\right)\mathrm{d}\mathrm{m}=\int \frac{150}{2\mathrm{m}+1}\mathrm{d}\mathrm{m}=75\ln \left|2\mathrm{m}+1\right|+\mathrm{C}$.

F(0) = C = 50.

Vậy F(m) = $75\ln \left|2\mathrm{m}+1\right|$ + 50.

Số người mắc bệnh ngày thứ 10 là F(10) = $75\ln \left|2.10+1\right|+50$ ≈ 278.

Bài 4.48 trang 21 SBT Toán 12 Tập 2: Một ô tô đồ chơi trượt xuống dốc và dừng sau 5 giây, vận tốc của ô tô đồ chơi từ thời điểm t = 0 giây đến t = 5 giây được cho bởi công thức v(t) = $\frac{1}{2}$t² – 0,1t³ (m/s).

Tính quãng đường ô tô đồ chơi đi đến khi dừng lại (làm tròn kết quả theo đơn vị mét đến số thập phân thứ hai).

Lời giải:

Quãng đường ô tô đồ chơi đi đến khi dừng lại là:

S(t) = $\underset{0}{\overset{5}{\int }}v\left(t\right)dt=\underset{0}{\overset{5}{\int }}\left(\frac{1}{2}{t}^2-0,1t^3\right)dt$

$=\left(\frac{t^3}{6}-\frac{0,1t^4}{4}\right){|}_0^5=\frac{5^3}{6}-\frac{0,{1.5}^4}{4}$≈ 5,21 (m).

Xem thêm Lời giải bài tập Toán 12 sách Kết nối tri thức hay, chi tiết khác:

Bài 14: Phương trình mặt phẳng

Bài 15: Phương trình đường thẳng trong không gian

Bài 16: Công thức tính góc trong không gian

Bài 17: Phương trình mặt cầu

Bài tập cuối chương 5